Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balakrishnan, J. S.
Çiperiani, M.
Lang, J.
Mirza, B.
and
Newton, R.
2016.
Directions in Number Theory.
Vol. 3,
Issue. ,
p.
33.
MATAR, AHMED
2016.
Selmer Groups and AnticyclotomicZp-extensions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 161,
Issue. 3,
p.
409.
Matar, Ahmed
2018.
Fine Selmer groups, Heegner points and anticyclotomic ℤp-extensions.
International Journal of Number Theory,
Vol. 14,
Issue. 05,
p.
1279.
Longo, Matteo
and
Vigni, Stefano
2019.
Plus/minus Heegner points and Iwasawa theory of elliptic curves at supersingular primes.
Bollettino dell'Unione Matematica Italiana,
Vol. 12,
Issue. 3,
p.
315.
Matar, Ahmed
2021.
Plus/minus Selmer groups and anticyclotomic $${{\mathbb {Z}}_p}$$-extensions.
Research in Number Theory,
Vol. 7,
Issue. 3,
LIM, Meng Fai
2021.
On the Weak Leopoldt Conjecture and Coranks of Selmer Groups of Supersingular Abelian Varieties in $p$-adic Lie Extensions.
Tokyo Journal of Mathematics,
Vol. 44,
Issue. 2,
Hatley, Jeffrey
Lei, Antonio
and
Vigni, Stefano
2022.
$$\Lambda $$-submodules of finite index of anticyclotomic plus and minus Selmer groups of elliptic curves.
manuscripta mathematica,
Vol. 167,
Issue. 3-4,
p.
589.
Lei, Antonio
Lim, Meng Fai
and
Müller, Katharina
2023.
Asymptotic formula for Tate–Shafarevich groups of p-supersingular elliptic curves over anticyclotomic extensions.
Advances in Mathematics,
Vol. 434,
Issue. ,
p.
109320.
Çiperiani, Mirela
2023.
Supersingular elliptic curves over ℤ𝑝-extensions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Castella, Francesc
and
Wan, Xin
2024.
Perrin-Riou’s main conjecture for elliptic curves at supersingular primes.
Mathematische Annalen,
Vol. 389,
Issue. 3,
p.
2595.
Kim, Byoung Du (BD)
2025.
Iwasawa Theory of elliptic curves at supersingular primes over higher rank Iwasawa extensions.
Journal of Number Theory,
Vol. 271,
Issue. ,
p.
189.
Işik, Erman
and
Lei, Antonio
2025.
The growth of Tate–Shafarevich groups of p$p$‐supersingular elliptic curves over anticyclotomic Zp${\mathbb {Z}}_p$‐extensions at inert primes.
Mathematika,
Vol. 71,
Issue. 4,

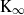 the anticyclotomic ℤ
the anticyclotomic ℤ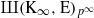 has trivial Λ-corank and, in the process, also show that
has trivial Λ-corank and, in the process, also show that  and
and 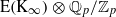 both have Λ-corank two.
both have Λ-corank two.