Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:00:29.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary cycles on Shimura curves and the Shimura lift II

Part of: Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  15 September 2014

Siddarth Sankaran
Siddarth Sankaran*
Affiliation:
Mathematisches Institut der Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany email sankaran@math.uni-bonn.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider two families of arithmetic divisors defined on integral models of Shimura curves. The first was studied by Kudla, Rapoport and Yang, who proved that if one assembles these divisors in a formal generating series, one obtains the 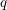$q$-expansion of a modular form of weight 3/2. The present work concerns the Shimura lift of this modular form: we identify the Shimura lift with a generating series comprising divisors arising in the recent work of Kudla and Rapoport regarding cycles on Shimura varieties of unitary type. In the prequel to this paper, the author considered the geometry of the two families of cycles. These results are combined with the Archimedean calculations found in this work in order to establish the theorem. In particular, we obtain new examples of modular generating series whose coefficients lie in arithmetic Chow groups of Shimura varieties.

Keywords

Shimura curvesspecial cyclesArakelov geometrymodular formsShimura lift

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties 14G40: Arithmetic varieties and schemes; Arakelov theory; heights 11F30: Fourier coefficients of automorphic forms
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 1963 - 2002
Copyright
© The Author 2014 

References

Bost, J. B., Potential theory and Lefschetz theorems for arithmetic surfaces, Ann. Sci. Éc. Norm. Supér. 32 (1999), 241–312.Google Scholar
Bruinier, J., Howard, B. and Yang, T., Heights of Kudla–Rapoport divisors and derivatives of L-functions, Preprint (2013) available at:http://www2.bc.edu/∼howardbe/Research/small-cm.pdf.Google Scholar
Cipra, B., On the Niwa–Shintani theta-kernel lifting of modular forms, Nagoya Math. J. 91 (1983), 49–117.Google Scholar
Gillet, H. and Soulé, C., Arithmetic intersection theory, Publ. Math. Inst. Hautes Études Sci. 72 (1990), 93–174.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. H., Tables of integrals, series and products, fifth edition, ed. Jeffrey, A. (Academic Press, Boston, 1995).Google Scholar
Howard, B., Intersection theory on Shimura surfaces, Compositio Math. 145 (2009), 423–475.CrossRefGoogle Scholar
Howard, B., Complex multiplication cycles and Kudla–Rapoport divisors, Ann. of Math. (2) 176 (2012), 1097–1171.Google Scholar
Howard, B., Complex multiplication cycles and Kudla–Rapoport divisors II, Amer. J. Math., to appear. Preprint (2013), available at:http://www2.bc.edu/∼howardbe/Research/unitary2.pdf.Google Scholar
Hriljac, P., Heights and Arakelov’s intersection theory, Amer. J. Math. 107 (1985), 23–38.Google Scholar
Kojima, H., Shimura correspondence of Maass wave forms of half integral weight, Acta Arith. 69 (1995), 367–385.Google Scholar
Kudla, S., Special cycles and derivatives of Eisenstein series, in Heegner points and Rankin L-series, Mathematical Sciences Research Institute Publications, vol. 49 (Cambridge University Press, Cambridge, 2004), 243–270.Google Scholar
Kudla, S. and Rapoport, M., Height pairings on Shimura curves and p-adic uniformization, Invent. Math. 142 (2000), 153–222.Google Scholar
Kudla, S. and Rapoport, M., Special cycles on unitary Shimura varieties I: unramified local theory, Invent. Math. 184 (2010), 629–682.CrossRefGoogle Scholar
Kudla, S. and Rapoport, M., Special cycles on unitary Shimura varieties II: global theory, J. Reine Angew. Math., to appear. Preprint (2009), arXiv:0912.3758.Google Scholar
Kudla, S., Rapoport, M. and Yang, T., Derivatives of Eisenstein series and Faltings heights, Compositio Math. 140 (2004), 887–951.Google Scholar
Kudla, S., Rapoport, M. and Yang, T., Modular forms and special cycles on Shimura curves, Annals of Mathematics Studies, vol. 161 (Princeton University Press, Princeton, NJ, 2006).Google Scholar
Lang, S., Introduction to Arakelov theory (Springer, New York, 1988).CrossRefGoogle Scholar
Niwa, S., Modular forms of half-integral weight and the integral of certain theta-functions, Nagoya Math. J. 56 (1975), 141–161.CrossRefGoogle Scholar
Sankaran, S., Special cycles on Shimura curves and the Shimura lift, PhD thesis, University of Toronto (2012).Google Scholar
Sankaran, S., Unitary cycles on Shimura curves and the Shimura lift I, Documenta Math. 18 (2013), 1403–1464.Google Scholar
Shimura, G., On modular forms of half integral weight, Ann. of Math. (2) 97 (1973), 440–481.Google Scholar
Shintani, T., On construction of holomorphic cusp forms of half-integral weight, Nagoya Math. J. 58 (1975), 83–126.Google Scholar
Vigneras, M.-F., Arithmetique des Algebres de Quaternions, Lecture Notes in Mathematics, vol. 800 (Springer, Berlin, 1980).Google Scholar
Vistoli, A., Intersection theory on algebraic stacks and their moduli spaces, Invent. Math. 97 (1989), 613–670.Google Scholar