1 Introduction
Sketches have long been associated with design. As part of the non-verbal thought of engineers, architects and artists, sketches are recognized as strongly contributing to the design process (Ferguson Reference Ferguson1992). In particular, early drawings are known for their capacity to enhance idea generation (Goldschmidt Reference Goldschmidt1991; Goel Reference Goel1995). However, if sketches can help designers to realize generativity by enhancing the variety and originality of their exploration, the nature of and reasons for this generativity remain difficult to understand; early sketches are indeed often comprehensible only to their maker (Goldschmidt Reference Goldschmidt1991) and cannot be easily translated into words (Ferguson Reference Ferguson1977). However, understanding the way sketches support design reasoning could provide interesting insights for design theory and practice.
Moreover, research on design, architecture and creativity has highlighted apparent contradictions concerning the contribution of sketches to design. First, early drawings are often presented as a useful tool that enhances the design process (Goldschmidt Reference Goldschmidt1991; Ferguson Reference Ferguson1992). If sketches constitute an essential work tool for designers, this is first because they allow the externalizing of ideas and information, therefore enhancing memory and thought (Goel Reference Goel1995; Suwa & Tversky Reference Suwa and Tversky1997; Tversky Reference Tversky, Gero and Tversky1999). However, sketching also offers instant feedback to the designer, who can very quickly evaluate and modify his or her ideas (Schön & Wiggins Reference Schön and Wiggins1992; Goldschmidt Reference Goldschmidt2003). Furthermore, drawings not only allow the processing of information, but are also important in accessing originality and novelty. Sketching indeed fosters reinterpretation during the individual thinking process (Van der Lugt Reference Van der Lugt2000, Reference Van der Lugt2002, Reference Van der Lugt2005) by providing the designer with new information (i.e., new ideas or knowledge), which enhances idea generation (Schön Reference Schön1983; Suwa et al. Reference Suwa, Tversky, Gero and Purcell2001). Although the cited studies highlight the positive effects of sketches on design reasoning, other research works on design and creativity have shown that sketching does not necessarily enhance the design process (Anderson & Helstrup Reference Anderson and Helstrup1993; McGown, Green & Rodgers Reference McGown, Green and Rodgers1998; Verstijnen et al. Reference Verstijnen, van Leeuwen, Goldschmidt, Hamel and Hennessey1998; Rodgers, Green & McGown Reference Rodgers, Green and McGown2000; Verstijnen et al. Reference Verstijnen, Heylighen, Wagemans and Neuckermans2001). Moreover, drawings sometimes have strong fixation effects, which adversely affect idea generation (Smith, Ward & Schumacher Reference Smith, Ward and Schumacher1993; Atilola, Tomko & Linsey Reference Atilola, Tomko and Linsey2015); sketches of potential ideas can indeed fix participants during a creativity task and decrease the originality of the ideas they will then generate.
To understand these multiple faces of sketching and the sketching activity, our research project aims to clarify the contribution of sketches to design reasoning; in which way do sketches interact with the design process and how may they help designers to generate original ideas? More precisely, we investigate how sketching might enhance designer’s generativity, which was defined by Hatchuel et al. (Reference Hatchuel, Le Masson, Reich and Weil2011) as the capacity to create novel propositions and can be modeled employing different design theories (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Weil2011). Generativity can take different forms as original ideas or new knowledge structures that support, afterwards, the creation of new proposals.
In this paper, we study three sequences of sketches relying on C–K design theory (Hatchuel & Weil Reference Hatchuel and Weil2003, Reference Hatchuel and Weil2009), which allows modeling of the design reasoning followed by the designer and how the sketches contribute to this reasoning. The three sequences were produced by an experienced architect, who was the head of the T/E/S/S engineering agency. In the analysis of results, the quantity of knowledge provided by the drawings is compared with the quantity of concepts generated. We especially study how the designer uses these new insights – concepts and knowledge – to lead his exploration, or in other words, how new information provided by the drawings interacts with the design process. Before presenting the results and their analysis, we will first provide a brief literature review on sketching, its effects in early design and its relation to the design process. Even if our study relies on sketches produced by an architect, our literature review does not only focus on research in the field of architecture; the review aims at presenting works addressing the contribution of sketches to the design reasoning, and therefore also relies on the literature in the fields of design and creativity.
2 Understanding sketching and its role in early design
2.1 Sketching: An essential work tool for designers
2.1.1 Sketches at various stages of the design process
The practice of drawing to support design activities has been developed since the Renaissance of the 15th century and originated in engineers’ and architects’ notebooks; drawings especially allowed the conveying of a vast amount of technical information through the diffusion of illustrated machine books and manuals of technical processes (Ferguson Reference Ferguson1977). Today, artists, architects and engineers still use sketches in their daily activities: ‘they execute a great number of drawings as a matter of standard practice’ (Goldschmidt Reference Goldschmidt1991). According to Goldschmidt (Reference Goldschmidt1991), drawings can be defined as ‘representations of either direct percepts, or ideas and images held in the mind’.
Often associated with the early stages of design, drawings can however intervene at various stages of the design process. In his book Engineering and the Mind’s Eye, Ferguson (Reference Ferguson1992) highlights the necessity of non-verbal thought for engineering and explains that drawings play a major role in the emergence of technological breakthroughs. He distinguishes three categories of sketches: ‘thinking sketches’ made by an engineer looking for new ideas, ‘talking sketches’ made when two engineers communicate and ‘prescriptive sketches’ that are meant to please and convince people outside of the design process. Even if these categories are named after properties of sketches (i.e., thinking, talking and prescriptive), the different categories are in fact based on stakeholders (i.e., the designer alone for the thinking sketch, two designers talking for the talking sketch and a designer with people outside of the design process for the prescriptive sketch). Therefore, a talking sketch in the sense used by Ferguson can be used in talking, but also to think or to convince. In the same way, idea generation is not to be associated only with thinking sketches but can also occur while working with talking or prescriptive sketches. According to Ferguson (Reference Ferguson1992), the generative power of drawings justifies their involvement at various stages of the design process.
2.1.2 Quick information processing
Sketching indeed offers many advantages that support design reasoning. Some studies show that sketching can enhance the thinking process by facilitating information processing: sketches indeed prove to be cognitive crutches, which allow an externalization of the designer’s ideas (Tversky Reference Tversky, Gero and Tversky1999). Because sketches differ in form and content from the object they represent, drawings are not however a presentation of a given idea but a certain representation of the idea (Suwa & Tversky Reference Suwa and Tversky1997). Moreover, the designer chooses which elements to put in his or her sketch; the designer can include important information regarding the explored subject or eliminate irrelevant information. Sketching thus constitutes an important cognitive tool. In particular, it improves memory and thought (Goel Reference Goel1995) and allows the rapid processing of visual and spatial information. Additionally, Schön & Wiggins (Reference Schön and Wiggins1992) point out that sketching offers instant feedback, which is economic cognitively. This quick information processing therefore enhances the design process and can increase the fluidity of the exploration. However, the fact that sketching accelerates exploration does not necessarily mean that sketching involves higher originality. In terms of how sketches may enhance the production of an original object, stronger generative effects might be involved.
2.2 Towards generative effects increasing originality
2.2.1 Sketching enhances reinterpretation
If Ferguson’s categories are based on stakeholders, the eponymous functions of these categories – thinking, talking and prescriptive functions – are actual functions of drawings associated with the design process. Van der Lugt (Reference Van der Lugt2000, Reference Van der Lugt2002, Reference Van der Lugt2005) studied how the use of sketches to represent concepts affects idea generation meetings. He identified three potential roles of drawing during idea generation. First, sketching could provide support for reinterpretation during the individual thinking process (in relation to a ‘thinking’ function). Second, sketching could support the reinterpretation of someone else’s drawings (in relation to a ‘talking’ function). Third, sketching could give better access to earlier ideas, thus fulfilling a ‘storing’ function. Van der Lugt compared two processes, namely traditional brainstorming and the brainsketching process, during which participants record ideas with sketches instead of post-it notes. In idea generation meetings involving industrial designers, it appears that brainstorming generates more ideas whereas brainsketching provides better access to earlier ideas and helps support reinterpretation during the individual thinking process. This reinterpretation enhances the creative process in that it corresponds to new ways of seeing a drawn representation and provides new directions for idea generation (Purcell & Gero Reference Purcell and Gero1998). Therefore, sketching not only helps to process and organize information: its role in reinterpretation suggests that it can also provide the designer with new information.
2.2.2 Generation of new insights
In a design-oriented context, sketching provides the designer with new insights and therefore promotes idea generation (Schön Reference Schön1983; Suwa et al. Reference Suwa, Tversky, Gero and Purcell2001). Freehand sketches are indeed often dense and ambiguous, which allows the designer to see new information and ideas in his or her drawings (Goel Reference Goel1995). In particular, the way that architects interact with their sketches has been described by Goldschmidt (Reference Goldschmidt1991, Reference Goldschmidt2003), who mentions a dialogue between the designer and the sketches; the architect reads new information in the drawings and thus enriches his or her reflection in response to this new information. In the case of sequences of sketches, invisible information is also present on paper, between the drawings (Goldschmidt Reference Goldschmidt2003). For example, different sketches can be related to one another; even if this relation is not visible on paper, it constitutes information included in the sequence of sketches. Moreover, Goldschmidt (Reference Goldschmidt1991) clarified this ability of sketches to bring new information by pointing out the role of depiction in idea generation; during ‘thinking loud’ sessions, architects were asked to express their thoughts while drawing and each sequence of statements was analyzed. It appears that two types of statements could be distinguished: ‘seeing that’ propositions and ‘seeing as’ propositions. The designer is ‘seeing as’ when he or she uses figural argumentation and ‘seeing that’ when he or she uses non-figural argumentation. For example, the designer sees his or her drawing ‘as’ a puzzle and sees ‘that’ this is a good way of solving the initial problem. Moreover, an alternation appears between ‘seeing as’ and ‘seeing that’ propositions. The role of ‘seeing as’ is to enable visual displays that help the designer to translate descriptive information into depiction. Meanwhile, depictive information can be used to extract original descriptive information, and thus provides the designer with new insights (Fish & Scrivener Reference Fish and Scrivener1990).
Sketching can thus enhance the design process by bringing new information and new ideas to the architect, which helps increase the originality of his or her exploration. However, these generative effects of sketching are not systematic and not even of the same nature, and it is not enough to sketch to enhance the creative process. In particular, Smith et al. (Reference Smith, Ward and Schumacher1993) showed that sketches may enhance fixation effects (Jansson & Smith Reference Jansson and Smith1991) by reducing the variety and originality of ideas generated during creativity sessions. If sketches of potential solutions are given to participants before an idea generation task, there may be strong fixation effects; in examples of drawings that contain familiar (unoriginal) features, the ideas generated will tend to include similar features, thus revealing a conformity effect. This is also true for the sketcher himself or herself. This is demonstrated by a famous anecdote where Itten asked his students at Bauhaus to sketch a lemon, and he was angry to find that they all drew the lemon without even trying to cut a slice and represent the acidity of the lemon (Itten Reference Itten1975). Boland & Collopy (Reference Boland and Collopy2004) also explained how the architect Franck Gehry pushed his young colleagues to avoid becoming trapped in their first sketch when creating a new building. Cognitive approaches have also shown that novice sketchers are not more creative when sketching (Anderson & Helstrup Reference Anderson and Helstrup1993; Verstijnen et al. Reference Verstijnen, van Leeuwen, Goldschmidt, Hamel and Hennessey1998, Reference Verstijnen, Heylighen, Wagemans and Neuckermans2001). Sketches can therefore affect idea generation either positively or negatively. This suggests that the ability of sketches to enhance creativity strongly depends on the design strategy followed by the designer.
2.3 Modeling the design strategy to identify generative effects of sketching
2.3.1 How the designer’s strategy affects the design quality
McGown et al. (Reference McGown, Green and Rodgers1998), Rodgers et al. (Reference Rodgers, Green and McGown2000) showed that the design strategy plays an important role in determining the efficiency of the sketching activity. By analyzing the sketches of an industrial designer, they studied the relation between the designer’s strategy to achieve novelty and the quality of his or her exploration. They especially focused on operations carried out to switch from one sketch to another. The design strategy was modeled by both lateral transformations and vertical transformations (Goel Reference Goel1995), where lateral transformations consist of movements from one idea to a different idea, whereas vertical transformations are movements from one idea to a more detailed version of the same idea. The study showed that not every sketched exploration led to generative effects. On the contrary, a quality and completed design is the result of design strategies that balance both lateral and vertical transformations. Lateral transformations often occur thanks to the ambiguity of sketches; ambiguity provides new insights to the designer (Goel Reference Goel1995) and helps change the direction of exploration. Therefore, if the designer wishes to achieve both variety and originality, his or her sketches should bring new insights, not just once but several times and at various stages of the design process. The results of the study (Goel Reference Goel1995) also suggest that design strategies can be less or more efficient, and perhaps, less or more controlled. It therefore appears important to precisely understand the nature of the interaction between the design strategy followed by the designer and the sketches that he or she generates during exploration. To do so, it is necessary to follow the design strategy used by the designer while sketching. In the studies of McGown et al. (Reference McGown, Green and Rodgers1998) and Rodgers et al. (Reference Rodgers, Green and McGown2000), design strategies were modeled by a succession of lateral and vertical transformations, but design strategies can also be modeled in several other ways.
2.3.2 Several ways of considering design strategies
A design strategy corresponds to a way of exploring an initial concept. One critical issue in this exploration is generativity (Hatchuel, Weil & Le Masson Reference Hatchuel, Weil and Le Masson2013). Generativity is the capacity to create novel proposals that are beyond the initial knowledge of the designer. The process of generativity is modeled employing design theories, which propose several forms of generativity (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Weil2011). Design theories have increased the understanding of generativity logics over time (Le Masson, Hatchuel & Weil Reference Le Masson, Hatchuel and Weil2011; Le Masson & Weil Reference Le Masson and Weil2013). Hence, there are many different design strategies that increase generativity. For instance, in creativity, divergent thinking and convergent thinking are distinguished to identify the type of design reasoning involved during the exploration; convergent thinking has the ability to give a single answer – the right answer – to a specific problem, whereas divergent thinking has the ability to provide a various panel of answers. Finding maximum alternative uses for an object, such as a brick or a toothbrush, is an example of a divergent-thinking exercise (Guilford Reference Guilford1950, Reference Guilford1967; Torrance Reference Torrance1962, Reference Torrance1966). In early design, divergent thinking will be encouraged to obtain a various panel of original ideas, whereas convergent thinking will be used during the evaluation and selection of ideas. The design strategy can thus be highlighted by the alternation between divergent-thinking and convergent-thinking stages. Moreover, the quality of individual divergent thinking can be assessed by the fluidity, variety and originality of ideas (Guilford Reference Guilford1950, Reference Guilford1967; Torrance Reference Torrance1962, Reference Torrance1966). Other metrics such as the novelty and quality of ideas (Shah, Smith & Vargas-Hernandez Reference Shah, Smith and Vargas-Hernandez2003) can also be developed to help measure the effectiveness of ideation. Moreover, studies have shown that the strategy used to explore different ideas may depend on the designer’s background (Lawson Reference Lawson1979) and on the designer’s experience (Cross Reference Cross2004).
Divergent thinking thus seems to be a common strategy for fostering generative effects in ideation. However, the exploration of knowledge is also important in furthering generativity. Indeed, Cropley (Reference Cropley2006) argues that exploring knowledge with convergent thinking is also necessary in producing new objects; divergent thinking needs a knowledge basis to operate and well-structured knowledge allows the exploration of variety in a relevant way. Le Masson, Hatchuel & Weil (Reference Le Masson, Hatchuel and Weil2016) indeed pointed out the generative power of knowledge organization; they showed that the courses of Itten and Klee at Bauhaus (Itten Reference Itten1961, Reference Itten1975; Klee Reference Klee1922, Reference Klee1966, Reference Klee2005) encouraged art students to build particular knowledge structures, which considerably enhance idea generation. In particular, Itten encouraged students to break existing determinisms between materials, colors and textures (such as ‘a cold gray metal’ or ‘a warm brown wood’), and this without making all combinations equivalent (i.e., no modularity); the students had to carefully choose and justify new associations. Models of generativity based on design theories (Hatchuel et al.
Reference Hatchuel, Le Masson, Reich and Weil2011) indeed show that, under certain conditions, working in terms of knowledge can lead to the production of new objects. Le Masson, Hatchuel and Weil explained in their study that the key to generativity actually lies in the structure of the knowledge basis, which is a direct consequence of the forcing theory proposed by Paul Cohen (Hatchuel, Weil & Le Masson Reference Hatchuel, Weil and Le Masson2013). The forcing theory presents a protocol with which to build completely new sets of objects (Cohen Reference Cohen1966, Reference Cohen2002). Without going deeply into mathematical details, the protocol starts with an initial set of objects ‘M’, where objects can be defined by a list of properties p, q, r, etc. (Figure 1). Such a list of properties, when the values of properties are defined, is called a filter. For example, a chair can be defined by different properties; e.g., its color (p
![]() $=$
blue) and material (q
$=$
blue) and material (q
![]() $=$
wood). A specific type of filter is obtained when filters intersect all dense subsets of M; dense subsets (D) are sets of properties that refine all existing properties of objects in M. For example, a chair can always be defined by its weight, price, or cost; even if a value can be zero (e.g., ‘a chair with zero weight’), the description of a chair can always be refined with those three dimensions, or in other words, constraints related to the weight (resp. cost or price) can always be added whatever the level of definition of the object. A filter intersecting all dense subsets D is described as being generic. The forcing theory of Cohen asserts that a generic filter potentially allows the definition of a set of completely new objects.
$=$
wood). A specific type of filter is obtained when filters intersect all dense subsets of M; dense subsets (D) are sets of properties that refine all existing properties of objects in M. For example, a chair can always be defined by its weight, price, or cost; even if a value can be zero (e.g., ‘a chair with zero weight’), the description of a chair can always be refined with those three dimensions, or in other words, constraints related to the weight (resp. cost or price) can always be added whatever the level of definition of the object. A filter intersecting all dense subsets D is described as being generic. The forcing theory of Cohen asserts that a generic filter potentially allows the definition of a set of completely new objects.

Figure 1. Forcing process in which a chair is defined by properties (also called ‘constraints’ in forcing theory). Middle: A filter of properties p, q defines a chair. Right: A generic filter is a filter that intersects all dense subsets; i.e., a set of properties that refine all known properties of objects. If the structure of properties follows the splitting condition, then the new object defined by the generic filter has the properties of chairs but is different from all already known chairs. This is the logic of generativity by forcing.

Figure 2. Example of a non-splitting basis (left and middle) and splitting basis (right). A knowledge basis is non-splitting when the set of properties (also called constraints) has either a deterministic relation (left) or a modular relation (middle). A knowledge basis is said to be splitting if and only if any constraint is always refined by at least two constraints (p is refined by q and
![]() $\text{q}^{\prime }$
) and these constraints are incompatible (i.e., no constraint like r refines both q and
$\text{q}^{\prime }$
) and these constraints are incompatible (i.e., no constraint like r refines both q and
![]() $\text{q}^{\prime }$
).
$\text{q}^{\prime }$
).
In fact, the generic filter will be completely new (i.e., out of M) if and only if the set of properties p, q, r, etc. meets the splitting condition, which avoids modularity and determinism within the space of properties. Examples of splitting and non-splitting structures of properties are given in Figure 2; a deterministic relation is a relation where a property q refines p with no possible alternatives (Figure 2, left) and a modular relation is a relation where a property r can refine either q or
![]() $\text{q}^{\prime }$
(Figure 2, middle). A structure with a modular or deterministic relation will constitute a non-splitting structure, whereas a structure presenting no modular or deterministic relations constitutes a splitting structure (Figure 2, right).
$\text{q}^{\prime }$
(Figure 2, middle). A structure with a modular or deterministic relation will constitute a non-splitting structure, whereas a structure presenting no modular or deterministic relations constitutes a splitting structure (Figure 2, right).
2.3.3 Studying the generative effects of sketching within the design process
To understand more precisely the mechanisms of the generative effects of sketches, it is necessary to better understand the design strategy followed by the designer and to identify the nature of the contribution provided by the sketching activity. We ask if sketching is generative. If it is, is sketching more related to ‘more ideas’ or ‘more knowledge’ (i.e., changes in the knowledge structure)? If the sketching is more based on new knowledge, does it mean that sketching helps create a ‘splitting knowledge base’?
In answering the questions posed above, we need an analytical framework based on a design theory to control the logic of generativity. Moreover, owing to the non-verbal aspect of drawings, we need to develop a dedicated methodology for the analysis of the contribution of sketches to the design process and to generativity. We describe a methodology that addresses these two issues below.
3 Methodology: Analyzing sketches with C–K theory
3.1 Selection of sketches
Our study considers three sequences of drawings produced by an experienced architect. The selected sketches come from the T/E/S/S engineering consulting agency, which comprises architects and engineers. The T/E/S/S agency is well known in the world of architecture for its breakthrough solutions, especially in façades design. It was notably involved in the design of the new Louis Vuitton Foundation in Paris and has developed an innovation approach around freehand sketching. We had full access to notebooks and sketches and were able to frequently meet experienced architects working for the agency. The present work focuses on the T/E/S/S agency because we believed that the sketches produced by experienced designers would be more helpful in clarifying the generative effects of sketches than sketches produced by people less experienced or less familiar with the activity of drawing for a design purpose (e.g., students in the field of art or architecture or non-expert drawers). For our analysis, we wanted sequences presenting original ideas because such sequences were more likely to show interesting generative effects of the sketching activity. To select sequences among those present in the notebooks, we also looked for different types of sketches; we thus selected two sequences of thinking sketches (made by an architect alone) and one sequence of talking sketches (made by the same architect talking with other architects). The first sequence (sequence 1) presents research for an innovative sun-shading device. The second sequence (sequence 2) presents an exploration that imagines an original bookcase for the agency. The third sequence (sequence 3) consists of the design of a new façade for a police station in Paris. These sequences correspond to the earlier stages of the design process and end with the emergence of an original idea. The first sequence consists of one page of a notebook (A5 format), the second sequence of six pages, and the third sequence of 20 pages. All three sequences were designed by the head architect of the T/E/S/S agency. The third sequence was produced during a meeting involving another architect of the T/E/S/S agency and two architects belonging to another company. The numbering of sequences is consistent with the chronological order of realization. To understand the design process associated with these series of sketches, we conducted several in-depth interviews with the architect; our aim was to understand the design reasoning of the architect at the time he generated the different sequences and then to analyze the interaction between the architect and his drawings. The architect was thus asked to explain his design reasoning when he was drawing. The interviews involved around six half-days of work and the entire study lasted one year; from September 2013 to September 2014. To avoid discrepancies arising because of the retrospective nature of the study, we selected sequences that were relatively new. However, the fact that the interviews were held after the production of the sketches may have resulted in small deviations from the actual design reasoning of the designer; the architect could indeed have forgotten elements about what his design reasoning really was when sketching.
3.2 C–K theory used to understand the generative effects of sketches
3.2.1 Design strategies as a co-expansion of concepts and knowledge
Highlighting the interaction between concepts and knowledge seems important to understanding the generative effects of sketches. In a more general way, the various contributions of sketching to design raise the issue of finding an integrated analytical framework that allows the analysis of generative processes. To address this issue, recent advances in design theory can be helpful. As shown by Hatchuel et al. (Reference Hatchuel, Le Masson, Reich and Weil2011, Reference Hatchuel, Weil and Le Masson2013), one unique feature of design theory is to model generativity by relying on formal structures. For instance, general design theory (Yoshikawa Reference Yoshikawa, Sata and Warman1981) models generativity with specific topological structures (Hausdorff spaces) whereas infused design (Shai & Reich Reference Shai and Reich2004) models generativity with duality properties in knowledge. In this paper, we rely on C–K design theory (Hatchuel & Weil Reference Hatchuel and Weil2003, Reference Hatchuel and Weil2009). There are several reasons for this methodological choice. First, the theory can be used with many types of knowledge because it is independent of the type of knowledge (Hatchuel & Weil Reference Hatchuel and Weil2002); it is only required that there is a logical status. Second, it accounts for many forms of generativity (Hatchuel et al. Reference Hatchuel, Le Masson, Reich and Weil2011). Third, in particular, it equally accounts for generativity that comes from the variety of ideas (C-expansion in C–K theory) and the generativity based on the structure of knowledge (K-expansion in C–K theory) (Le Masson et al. Reference Le Masson, Hatchuel and Weil2016). Fourth, C–K theory is already widely used as an analytical framework in studying empirical design situations and particularly generativity in these situations. It is thus an analytical tool that is well tried and proven (Agogué & Kazakçi Reference Agogué, Kazakçi, Chakrabarti and Blessing2014; Hatchuel et al. Reference Hatchuel, Le Masson, Weil, Agogué, Kazakçi, Hooge, Chakrabarti and Lindemann2015).
In C–K design theory, generativity is modeled as expansions in knowledge (K) and expansions in concepts (C), where knowledge refers to statements with a logical status – the statement is either true or false, the object exists or does not – whereas concepts refer to statements without logical status, meaning it is impossible to say if the statement is true or false, or if the object exists or not. For example, ‘puzzles’ are common knowledge, but a ‘building as a puzzle’ is a concept. In C–K theory, the concept space (or C-space) and the knowledge space (or K-space) are represented as shown in Figure 3. The concepts are necessarily organized in a tree structure (which is a theorem of the theory), whereas knowledge can be represented in many ways because knowledge is a ‘free parameter’ of the theory (Hatchuel et al. Reference Hatchuel, Weil and Le Masson2013), which allows the theory to be used with multiple knowledge structures (see, for example, Le Masson et al. (Reference Le Masson, Hatchuel, Kokshagina and Weil2015a )).

Figure 3. C–K theory: Representation of C-space and K-space.
Moreover, the theory distinguishes four operators to model moves within the C- and K-spaces: K-
![]() ${>}$
C, C-
${>}$
C, C-
![]() ${>}$
C, K-
${>}$
C, K-
![]() ${>}$
K and C-
${>}$
K and C-
![]() ${>}$
K. The exploration of concepts and the exploration of knowledge constantly work together; starting from the concept of ‘a building as a puzzle’, both already acquired knowledge and new knowledge are needed to know what such a building could be in practice. The initial concept can then be specified with other sub-concepts. The designer can choose to explore very different concepts or to focus on one particular path. In both cases, additional knowledge will be needed to continue exploring the original topic until a completed design appears. Therefore, an exploration will be generative if it leads to an expansion of knowledge and/or an expansion of concepts.
${>}$
K. The exploration of concepts and the exploration of knowledge constantly work together; starting from the concept of ‘a building as a puzzle’, both already acquired knowledge and new knowledge are needed to know what such a building could be in practice. The initial concept can then be specified with other sub-concepts. The designer can choose to explore very different concepts or to focus on one particular path. In both cases, additional knowledge will be needed to continue exploring the original topic until a completed design appears. Therefore, an exploration will be generative if it leads to an expansion of knowledge and/or an expansion of concepts.
Modeling this alternation between knowledge exploration and concept exploration moreover allows the differentiation of several types of design strategies (Hatchuel, Le Masson & Weil Reference Hatchuel, Le Masson and Weil2004; Kroll, Le Masson & Weil Reference Kroll, Le Masson and Weil2014). Some strategies can be described as concept-oriented strategies, in which most new knowledge is directly used to generate new concepts (Figure 4, left). There are also knowledge-oriented strategies, in which most knowledge does not directly affect the C-space. Instead, new knowledge involves a reorganization of knowledge (or knowledge reordering), therefore affecting first the K-space (Figure 4, right). Once new rules appear in the knowledge space, new paths of innovation can be opened (Le Masson et al. Reference Le Masson, Hatchuel, Kokshagina and Weil2015a ). More specifically, we know that generativity is higher if the knowledge structure follows the splitting condition. Hence, one can analyze how knowledge expansions change the knowledge structure to increase generativity (Lenfle, Le Masson & Weil Reference Lenfle, Le Masson and Weil2016).
Hence, in the analytical framework based on C–K theory, we will follow the creation of concepts and the creation of knowledge, and, in the case of knowledge creation, we will examine how knowledge creation changes knowledge structures.

Figure 4. Two ways of generating concepts: direct use of knowledge (left) and knowledge reordering (right).
3.2.2 Analyzing design strategies associated with sketches using C–K theory
To better understand the generative effects produced by sketching activity, we analyzed a given phenomenon; i.e., the interaction between an architect and his sketches. We had access to the sketches (D) and to the explanations of the architect (A) (Figure 5). A theoretical framework still had to be chosen to analyze such data and to better understand the design strategy followed by the architect. In this context, C–K design theory was used to model the alternation between concepts (C) and knowledge (K) involved in the sequences of sketches. The interaction between A (architect) and D (sketches) constitutes a design space.

Figure 5. C–K theory as an analytical framework used to study a specific phenomenon, namely the interactions between the architect (A) and his sketches (D). Left: The design space with A interacting with his own sketch D. Right: A modeled as a C–K agent, with the interactions between A and D thus becoming C
![]() $\rightarrow$
D, K
$\rightarrow$
D, K
![]() $\rightarrow$
D and D
$\rightarrow$
D and D
![]() $\rightarrow \unicode[STIX]{x2202}$
C and D
$\rightarrow \unicode[STIX]{x2202}$
C and D
![]() $\rightarrow \unicode[STIX]{x2202}$
K.
$\rightarrow \unicode[STIX]{x2202}$
K.
During the exploration led by the architect, knowledge related to the topic concerned and knowledge unrelated to the topic concerned may have been mobilized. This is why we choose to distinguish K-elements related to the ongoing exploration (e.g., architectural elements related to the initial topic, aesthetic expectations and evaluation criteria such as stability and costs) and knowledge that appears unrelated to the initial topic. For example, the knowledge ‘puzzle’ in our previous example does not appear to be directly related to an exploration around buildings. We thus note K* knowledge that appears distant from the initial topic (or initial concept C0), whereas K will refer to knowledge belonging to the knowledge basis related to the topic.
Using C–K theory as an analytical framework, the four following types of interactions between the architect and his sketch are possible.
-
(i) K(*)-
 ${>}$
D: This operator corresponds to a situation where the architect puts knowledge that he had already in mind into a sketch to, for instance, visualize or even test the knowledge. This knowledge can be less or more related to the original concept C0.
${>}$
D: This operator corresponds to a situation where the architect puts knowledge that he had already in mind into a sketch to, for instance, visualize or even test the knowledge. This knowledge can be less or more related to the original concept C0. -
(ii) C-
 ${>}$
D: This operator allows a concept imagined by the designer to be transferred into a sketch. Since concepts have a non-logical status, this operator could help clarify concepts by visualization.
${>}$
D: This operator allows a concept imagined by the designer to be transferred into a sketch. Since concepts have a non-logical status, this operator could help clarify concepts by visualization. -
(iii) D-
 ${>}$
K(*): This operator corresponds to a situation where the sketch brings new knowledge to the designer, knowledge he did not have previously when mentally thinking about the initial subject. This knowledge can be less or more related to the original concept C0.
${>}$
K(*): This operator corresponds to a situation where the sketch brings new knowledge to the designer, knowledge he did not have previously when mentally thinking about the initial subject. This knowledge can be less or more related to the original concept C0. -
(iv) D-
 ${>}$
C: With this operator, the sketch directly generates a concept; i.e., a proposition with a non-logical status. (For example, the architect sees a ‘building as a puzzle’ in his drawing.)
${>}$
C: With this operator, the sketch directly generates a concept; i.e., a proposition with a non-logical status. (For example, the architect sees a ‘building as a puzzle’ in his drawing.)
In analyzing the sequences of sketches, the architect was asked to comment on the different sketches by explaining what his reasoning was while drawing. The architect had no background in design theory and was not asked to model his reasoning with C–K theory: he only provided statements of what he was thinking and doing. Different interviews were analyzed after each work session. Additional interviews were required each time this analysis showed remaining gaps in the reconstructed design reasoning of the architect. During the analysis, each sketch was associated with statements made by the architect and these statements were qualified as either concepts or knowledge. It is noted that the K and C statuses, and thus the design reasoning modeling, are strongly related to the designer’s reference frame; a concept is indeed always considered as such given a specific knowledge basis. In our study, a statement that is a concept for the architect may be knowledge for someone else (and vice versa; a statement that is knowledge for the architect may be a concept for others). An example of the analysis of sketches is presented below (Figure 6 and Table 1).

Figure 6. Sequence 1 for an innovative sun-shading device.
Table 1. Sequence 1: Related statements, K or C status, and related operators

For each sequence of drawings, the succession of operators was established to draw the design strategy (Table 1). Whereas the four classical operators (K-
![]() ${>}$
C, C-
${>}$
C, C-
![]() ${>}$
C, K-
${>}$
C, K-
![]() ${>}$
K and C-
${>}$
K and C-
![]() ${>}$
K) describe what happens in the designer’s mind alone, the four additional operators (K(*)-
${>}$
K) describe what happens in the designer’s mind alone, the four additional operators (K(*)-
![]() ${>}$
D, C-
${>}$
D, C-
![]() ${>}$
D, D-
${>}$
D, D-
![]() ${>}$
K(*), D-
${>}$
K(*), D-
![]() ${>}$
C) describe the interaction between the designer’s mind and sketch. The number of K-
${>}$
C) describe the interaction between the designer’s mind and sketch. The number of K-
![]() ${>}$
D, C-
${>}$
D, C-
![]() ${>}$
D, D-
${>}$
D, D-
![]() ${>}$
K and D-
${>}$
K and D-
![]() ${>}$
C operators was summarized to help visualize the occurrences of the operators and explain the effect of sketches on the design process. Our analysis of the results does not search for differences among the three sequences; we will look for similar patterns in the sequences that help explain the way sketches tend to contribute to the design process. The final results of the analysis were shown and explained to the architect to verify that they were consistent with his general feelings about his design strategy.
${>}$
C operators was summarized to help visualize the occurrences of the operators and explain the effect of sketches on the design process. Our analysis of the results does not search for differences among the three sequences; we will look for similar patterns in the sequences that help explain the way sketches tend to contribute to the design process. The final results of the analysis were shown and explained to the architect to verify that they were consistent with his general feelings about his design strategy.
4 Results: New knowledge and knowledge organization that supports the design strategy
4.1 Succession and occurrence of different operators
Table 2 presents the succession of operators for the three sequences. In the ‘operators’ succession’ column, the double slash // corresponds to a change of sketch. The table also summarizes the occurrence of each operator in relation to the D-space (K-
![]() ${>}$
D, C-
${>}$
D, C-
![]() ${>}$
D, D-
${>}$
D, D-
![]() ${>}$
K, D-
${>}$
K, D-
![]() ${>}$
C) for each sequence.
${>}$
C) for each sequence.
Table 2. Succession and occurrence of operators

4.2 Role of sketches in the design process
4.2.1 Not only a representation of existing ideas
Sketches could be seen as a means to visualize ideas that the architect already had in mind; i.e., existing concepts or already acquired knowledge. Following this assumption, a majority of C-
![]() ${>}$
D and K-
${>}$
D and K-
![]() ${>}$
D operations could be expected. This would correspond to a situation where sketches would not have strong generative effects, as they would not provide the architect with many new insights – concepts or knowledge. However, in the three sequences, not only C-
${>}$
D operations could be expected. This would correspond to a situation where sketches would not have strong generative effects, as they would not provide the architect with many new insights – concepts or knowledge. However, in the three sequences, not only C-
![]() ${>}$
D and K-
${>}$
D and K-
![]() ${>}$
D, but also D-
${>}$
D, but also D-
![]() ${>}$
C and D-
${>}$
C and D-
![]() ${>}$
K operations occurred. Figure 7 presents the distribution of the different operators; sketches refer most of the time to both concepts and knowledge statements. This is consistent with the explanation in the literature that the contribution of sketches in the design process goes beyond the representation of existing ideas (Schön Reference Schön1983; Suwa et al.
Reference Suwa, Tversky, Gero and Purcell2001; Van der Lugt Reference Van der Lugt2002, Reference Van der Lugt2005).
${>}$
K operations occurred. Figure 7 presents the distribution of the different operators; sketches refer most of the time to both concepts and knowledge statements. This is consistent with the explanation in the literature that the contribution of sketches in the design process goes beyond the representation of existing ideas (Schön Reference Schön1983; Suwa et al.
Reference Suwa, Tversky, Gero and Purcell2001; Van der Lugt Reference Van der Lugt2002, Reference Van der Lugt2005).

Figure 7. Occurrence of operators.

Figure 8. Set of sun-shading devices for the police station’s façade (front view, sequence 3). Black lines are the main lines of the wall and sun-shading devices. Red lines are newly added lines that produce ‘vegetal cells’.
The architect puts a lot into his sketches – not only concepts but also knowledge. On the one hand, the K-
![]() ${>}$
D operations correspond to the use of knowledge; e.g., in sequence 1, the architect is testing an H-shaped structure to see if such a structure will suit him (Table 1). On the other hand, the C-
${>}$
D operations correspond to the use of knowledge; e.g., in sequence 1, the architect is testing an H-shaped structure to see if such a structure will suit him (Table 1). On the other hand, the C-
![]() ${>}$
D operations show an attempt to visualize and refine concepts. For example, the architect had in mind the concept of ‘an original clipping system that fixes plates and the structure by the sides’; he tested the concept by making a sketch, and since the test was successful, a conjunction appears (Table 1). However, the architect also receives much knowledge and many concepts from his sketches with the D-
${>}$
D operations show an attempt to visualize and refine concepts. For example, the architect had in mind the concept of ‘an original clipping system that fixes plates and the structure by the sides’; he tested the concept by making a sketch, and since the test was successful, a conjunction appears (Table 1). However, the architect also receives much knowledge and many concepts from his sketches with the D-
![]() ${>}$
K and D-
${>}$
K and D-
![]() ${>}$
C operations. Even though they are provided by the sketch, the K- and C-elements are not necessarily new concepts or new knowledge. They can be knowledge and concepts that the designer had previously when mentally thinking about the initial concept; e.g., several D-
${>}$
C operations. Even though they are provided by the sketch, the K- and C-elements are not necessarily new concepts or new knowledge. They can be knowledge and concepts that the designer had previously when mentally thinking about the initial concept; e.g., several D-
![]() ${>}$
K operations correspond to an evaluation made by the designer looking at his sketch. In this way, several K-elements brought by the sketches belonged to the initial basis of the architect, which will be noted K0 (and includes knowledge on regulation, aesthetic requirements and personal expectations). Nevertheless, many D-
${>}$
K operations correspond to an evaluation made by the designer looking at his sketch. In this way, several K-elements brought by the sketches belonged to the initial basis of the architect, which will be noted K0 (and includes knowledge on regulation, aesthetic requirements and personal expectations). Nevertheless, many D-
![]() ${>}$
K operations correspond to new knowledge in that the architect sometimes reads in his sketches knowledge that he did not have previously in mind; i.e., knowledge outside the K0 basis. This new knowledge is sometimes a K-element related to the initial topic, but can also be a K*-element that appears distant from the initial topic; e.g., in sequence 3, looking for an innovative façade for a police station, the architect saw living cells (K*) in a drawing of sun-shading devices (Figure 8). Moreover, some of these D-
${>}$
K operations correspond to new knowledge in that the architect sometimes reads in his sketches knowledge that he did not have previously in mind; i.e., knowledge outside the K0 basis. This new knowledge is sometimes a K-element related to the initial topic, but can also be a K*-element that appears distant from the initial topic; e.g., in sequence 3, looking for an innovative façade for a police station, the architect saw living cells (K*) in a drawing of sun-shading devices (Figure 8). Moreover, some of these D-
![]() ${>}$
K operations generated a concept following a D-
${>}$
K operations generated a concept following a D-
![]() ${>}$
K-
${>}$
K-
![]() ${>}$
C succession (D-
${>}$
C succession (D-
![]() ${>}$
K, then K-
${>}$
K, then K-
![]() ${>}$
C); in the sketch of Figure 8, the architect saw a ‘bulk breaking’ (K) for the last pole. He chose to explore the idea of a ‘façade with bulk breakings’ (C) in the following drawings. Finally, new concepts were directly read from the sketches (D-
${>}$
C); in the sketch of Figure 8, the architect saw a ‘bulk breaking’ (K) for the last pole. He chose to explore the idea of a ‘façade with bulk breakings’ (C) in the following drawings. Finally, new concepts were directly read from the sketches (D-
![]() ${>}$
C); looking at the red lines of Figure 8, the designer realized that there could be a second system in the façade (C), which would be less visible than the first system he was dealing with (the poles in black in Figure 8) and could form ‘vegetal cells’ when combined with the first system. However, he did not know exactly what these two different systems could be in practice.
${>}$
C); looking at the red lines of Figure 8, the designer realized that there could be a second system in the façade (C), which would be less visible than the first system he was dealing with (the poles in black in Figure 8) and could form ‘vegetal cells’ when combined with the first system. However, he did not know exactly what these two different systems could be in practice.
4.2.2 A significant amount of knowledge
Thus, sketching allows the designer to read new insights in his sketches. Since the earlier stages of the architectural design are often associated with fuzzy drawings and fuzzy ideas, it can be expected that early sketches refer mostly to concepts rather than knowledge. However, the very high number of K-
![]() ${>}$
D and D-
${>}$
D and D-
![]() ${>}$
K operators (Table 2 and Figure 7) shows that the architect plays mostly with knowledge rather than concepts. Moreover, an appreciable number of new K-elements prove to be distant from the original topic (K*-elements). In the bookcase sequence, this is the case for the Chinese motif and cables: these two K*-elements do not appear directly related to the bookcase topic. Similarly, knowledge on biological cells is introduced in sequence 3. In each sequence, the number of D-
${>}$
K operators (Table 2 and Figure 7) shows that the architect plays mostly with knowledge rather than concepts. Moreover, an appreciable number of new K-elements prove to be distant from the original topic (K*-elements). In the bookcase sequence, this is the case for the Chinese motif and cables: these two K*-elements do not appear directly related to the bookcase topic. Similarly, knowledge on biological cells is introduced in sequence 3. In each sequence, the number of D-
![]() ${>}$
K* operations is significant in comparison with the total number of D-
${>}$
K* operations is significant in comparison with the total number of D-
![]() ${>}$
K operators (Table 2, Figure 7). Surprisingly, sketches thus have the ability to help the designer mobilize knowledge that he would not have spontaneously mobilized in the first place. In other words, sketches allow the mobilization of knowledge not directly related to C0 or even the ongoing exploration.
${>}$
K operators (Table 2, Figure 7). Surprisingly, sketches thus have the ability to help the designer mobilize knowledge that he would not have spontaneously mobilized in the first place. In other words, sketches allow the mobilization of knowledge not directly related to C0 or even the ongoing exploration.
The architect therefore seems to have followed a knowledge-oriented design strategy. Indeed, in the three sequences, the concepts generated by the architect do not result from the refinement of an initial concept; there are few C-
![]() ${>}$
C operations in the three sequences and it is often difficult to see the logical connections between the different concepts. Thus, the sketches are not the result of an exploration of the C-space. For example, when exploring solutions for a new bookcase for the agency, the architect reached the solution circled at the bottom of Figure 9. The solution is a bookcase consisting of motifs in the form of a ‘T’ connected by two junction points. None of the previous drawings presents the ‘T’ motif or the idea of two junction points between motifs. The solution seems to have come from nowhere. If the final concept does not result from the exploration of the C-space, the explanation must lie in the knowledge space. The exploration of knowledge therefore has to be analyzed.
${>}$
C operations in the three sequences and it is often difficult to see the logical connections between the different concepts. Thus, the sketches are not the result of an exploration of the C-space. For example, when exploring solutions for a new bookcase for the agency, the architect reached the solution circled at the bottom of Figure 9. The solution is a bookcase consisting of motifs in the form of a ‘T’ connected by two junction points. None of the previous drawings presents the ‘T’ motif or the idea of two junction points between motifs. The solution seems to have come from nowhere. If the final concept does not result from the exploration of the C-space, the explanation must lie in the knowledge space. The exploration of knowledge therefore has to be analyzed.

Figure 9. Extracts from sequence 2 for the bookcase (in order of achievement). The final solution is at the bottom right in sketch 7 and is a bookcase consisting of motifs in the form of a ‘T’ connected by two junction points. None of the previous drawings presents the ‘T’ motif or the idea of two junction points between motifs.
4.3 Generative effects of knowledge preordering
If the generative effects obtained rely on the K-space, the theory says that there are two ways of generating concepts (cf. Figure 4). On the one hand, new knowledge may be directly used to generate a new concept with a K-
![]() ${>}$
C operation: this is what happens in sequence 3 when the architect sees a ‘bulk breaking’ (K), which generates the concept of a ‘façade with bulk breakings’ (C). On the other hand, new knowledge can involve a reordering of the knowledge space; it does not affect the C-space first, but the K-space. Thanks to a restructuring of the K-space, new rules appear and open new paths of innovation. In practice, once the knowledge basis is reorganized, the designer does not need to generate all the alternative concepts or to further explore the C-space: he or she just has to pick one concept. Moreover, it has already been explained that a generative way of reorganizing knowledge is to build a splitting knowledge basis by eliminating all modular or deterministic relations in the K-space (cf. Figure 2).
${>}$
C operation: this is what happens in sequence 3 when the architect sees a ‘bulk breaking’ (K), which generates the concept of a ‘façade with bulk breakings’ (C). On the other hand, new knowledge can involve a reordering of the knowledge space; it does not affect the C-space first, but the K-space. Thanks to a restructuring of the K-space, new rules appear and open new paths of innovation. In practice, once the knowledge basis is reorganized, the designer does not need to generate all the alternative concepts or to further explore the C-space: he or she just has to pick one concept. Moreover, it has already been explained that a generative way of reorganizing knowledge is to build a splitting knowledge basis by eliminating all modular or deterministic relations in the K-space (cf. Figure 2).
Given that the succession of operators in Table 2 shows only a few K-
![]() ${>}$
C operations (i.e., two among 15 operators for sequence 1, six among 44 for sequence 2, and 12 among 61 for sequence 3), it may be inferred that generativity rather comes from the second process (knowledge reorganization). The confirmation of this assumption requires a more accurate analysis of how the architect uses knowledge to reach generative effects by realizing a splitting knowledge base.
${>}$
C operations (i.e., two among 15 operators for sequence 1, six among 44 for sequence 2, and 12 among 61 for sequence 3), it may be inferred that generativity rather comes from the second process (knowledge reorganization). The confirmation of this assumption requires a more accurate analysis of how the architect uses knowledge to reach generative effects by realizing a splitting knowledge base.
4.3.1 A strategically built knowledge space
In our study, the architect organizes a strategically built knowledge space, where each K-element is carefully selected, tested and, if necessary, removed. For instance, in the second sequence, the architect wanted the bookcase to have glass tile integration and to reflect the agency’s identity. Figure 10 presents drawings of the sequence and effect on the K-space. To facilitate understanding, K0 has been distinguished and other knowledge bases have been simplified. The representation of the knowledge space here does not aim at being exhaustive; we provide only the knowledge bases involved in the part of the reasoning that is described below.

Figure 10. Effects of drawings on the K-space organization. Left: Drawings of the ‘bookshelf’ sequence. Right: Effect of these sketches on the architect K-space.
On several occasions, the architect reads original knowledge in his sketches and chooses to test it; e.g., in the first sketch, the designer sees a Chinese motif that appears to be stable thanks to intertwining lines. The designer chooses to work with this motif throughout the sequence (second and fifth drawings) and keeps this new knowledge in his K-basis. In the second sketch, he is testing alternatives of the interlacing patterns by introducing rounded edges. However, the aesthetic of the result does not please him, he realizes that glass integration will be technically difficult with round edges and he removes the curved lines from his K-basis. He then produces several drawings and, when observing the third sketch, he sees a linear form that makes him consider using cables. Here again, he chooses to test this new knowledge as we can see in the fourth drawing. However, looking at this sketch, he realizes that cables do not allow glass integration over the entire surface of the library; he thus gives up on the idea of cables and withdraws this element from his K-basis.
Knowledge is thus carefully organized before reaching the final concept. Such organization is thus referred to as ‘knowledge preordering’. If this preordering of knowledge allows the change of one or several paradigms of the initial knowledge basis, it is expected that the generative effects of sketches come from the effect of new knowledge on the knowledge structure itself (and not on the C-space). It therefore has to be shown that new knowledge affects the knowledge structure in a generative way through, for instance, the creation of a splitting structure.
4.3.2 Knowledge preordering leading to generativity
The effect of new knowledge on the structure of the K-basis is analyzed on the basis of several examples from sequences 2 and 3. In sequence 2, the cables are an example of K* that the designer chooses to definitively draw aside of the exploration, as soon as he realizes that this K*-element does not allow the fulfillment of one of his requirements. In fact, the K*-element ‘cables’ involves determinism in the K-basis since it forbids the use of another piece of knowledge, namely the glass tiles (Figure 10). In the same way, the curved lines that the architect removed from his K-basis are both modular and deterministic; modular because they can be added on each motif, and deterministic because they do not allow glass integration and do not please the architect in terms of aesthetics. In contrast, the architect keeps the intertwining motif in his K-basis. This K*-element allows the creation of interdependence (no modularity) in the K-basis without involving determinism: with an intertwining motif, the stability, the glass integration and the requirements about the agency’s identity become strongly linked to one another. A stable intertwining motif can allow glass integration and respect the firm identity (no determinism) but not every stable intertwining motif allows the fulfillment of these requirements (no modularity). Therefore, the architect proceeds to a knowledge preordering that eliminates both modularity and determinism (Figure 11).
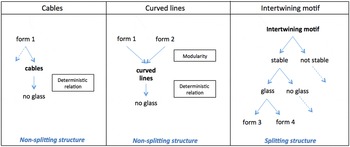
Figure 11. Avoiding modularity and determinism in building ‘splitting’ knowledge structures.
Such a process corresponds to the constitution of a splitting knowledge basis and is similar to a forcing protocol, which could explain the generativity of the architect’s design reasoning. In our case, the building of a splitting knowledge basis by removing all modular or deterministic relations allows the introduction of new rules in the K-space, and therefore fosters the production of a completely new object. For example, the intertwining motif completely changes the way the architect sees the bookcases. The common bookcase corresponds indeed to an intersection of vertical and horizontal lines. Such a pattern is both modular and deterministic for the architect; no matter the number of compartments, the bookcase would always be stable and could integrate glass tiles (i.e., it is modular), yet it does not correspond to the firm identity (i.e., it is deterministic). The introduction of the intertwining motif changes the rules by linking the stability, the respect of the firm identity and the glass integration. All common knowledge about bookcases and the ways of building bookcases has to be reevaluated in the light of this new rule. The reorganization of knowledge that follows then allows the generation of several original concepts that could not have emerged under the previous rules. This structuration of a splitting knowledge basis that changes the rules of the knowledge space is also seen for sequence 3; from the moment the architect sees living cells (K*) in his drawing (Figure 9), he stops considering the sun-shading devices have lines or ‘trees’, and begins to organize the façade by drawing rectangles that represent the space where the sun-shading devices are not. Here again, the final concept comes from the creation of new rules (or a new algebra) for the knowledge space.
The process of knowledge preordering thus allows the generation of several concepts and presents an alternative to the traditional use of knowledge in concept generation. Moreover, the organization of a splitting knowledge basis contributes to the explanation of the generative power of sketches; sketching helps the architects mobilize knowledge that sometimes appears distant from the initial topic. Such knowledge helps create interdependence in the knowledge basis without involving determinism. This produces new rules in the knowledge space and opens new innovative paths.
5 Conclusion
The present study developed a dedicated methodology using C–K theory to better understanding the generative effects of sketching. The study of three sequences of sketches, which were produced by an experienced architect when searching for new and original ideas, confirmed that sketches not only are a representation of ideas that the designer already has in mind but can indeed provide the designer with both new concepts and new knowledge. In particular, the new insights brought by the sketches prove to be mostly knowledge. The architect thus follows a knowledge-oriented strategy and not a concept-oriented strategy as might be expected. Moreover, sketches have the ability to help the designer mobilize knowledge that he or she would not have spontaneously related to the initial topic. Such knowledge helps the architect to conduct an important work of knowledge structuration called knowledge preordering. In this way, the designer constitutes a splitting knowledge basis, which increases his or her generative capacity.
The present study is limited in that it is a single case study (even if it is based on three sketching sequences). Still, it provides a counterexample to models of generativity by sketching that are too simple. This counterexample has the following theoretical implications.
-
(1) Sketching is not limited to the expression of a preformed mental image.
-
(2) Sketching is not limited to ideation but also relates to knowledge and knowledge creation.
-
(3) Sketching is not limited to provide a synthesis of pre-existing knowledge. It is not related to the activation of existing expertise; it helps create specific structures in knowledge, a splitting knowledge base.
-
(4) Sketching might support a form of analogy (Goldschmidt Reference Goldschmidt, Eastman, McCracken and Newstetter2001; Davies, Goel & Nersessian Reference Davies, Goel and Nersessian2009) but our example shows that analogies are created with the specific purpose of creating particular knowledge structures.
The present study hence clarifies a specific design strategy relying on sketching; i.e., the architect creates a splitting knowledge base by sketching. It was already known that architects and designers use sketching to make analogies (Goldschmidt Reference Goldschmidt, Eastman, McCracken and Newstetter2001; Davies et al. Reference Davies, Goel and Nersessian2009). It is also known that making an analogy is a complex process and that there are many forms and types of analogies that are more or less ‘generative’ (Hofstadter & Sander Reference Hofstadter and Sander2013). This leads to the proposal that the ‘sketching for splitting knowledge’ process might appear as a specific form of analogy with a specific generative power. This paves the way to further research.
Beyond presenting the case of a single designer, the present study contributes to clarifying the logic of generativity through knowledge expansion. The study of the architect echoes works done on generativity at Bauhaus (Le Masson et al. Reference Le Masson, Hatchuel and Weil2016) or generativity in breakthrough engineering projects (Lenfle et al. Reference Lenfle, Le Masson and Weil2016). These works highlight the importance of knowledge structuration in idea generation: the efficiency of knowledge preordering appears closely linked to the nature of new knowledge. In our study, new knowledge involving originality consists of elements breaking existing rigidities in the knowledge basis; i.e., classical rules such as modularity and determinism. The introduction of knowledge distant from the initial topic is thus no mere coincidence; it follows from the very knowledge structure that was related to the topic in the first place.
The above has clear theoretical implications (see also Le Masson, Reich & Subrahmanian (Reference Le Masson, Reich and Subrahmanian2015b )): in design, the logic of knowledge creation for generativity tends to create knowledge that is non-determinist and non-modular, which means that this knowledge is independent from what was known before. This paves the way to a theoretical analysis of the value of knowledge in design: the value of knowledge is not only in rules, ontologies, variants, algebra and integrated structures but also in the independences in knowledge structures. Additionally, the value of independences contradicts common sense coming from information theory. In information theory, one expects that a variable X will allow learning for a variable Y; hence, one expects that Y and X are strongly correlated. If X and Y are independent, then X does not provide any information for Y, and X is thus useless to Y. In contrast, the knowledge structure that meets the splitting condition actually corresponds to the fact that when X and Y are independent, X can provide important original information to the design of a new Y – precisely because this information was not present in the ‘old’ Y.
More specifically, from the above theoretical perspective, one can underline a specific issue: in this paper, generativity follows from the forcing protocol, as already shown in the literature (Hatchuel et al. Reference Hatchuel, Weil and Le Masson2013; Le Masson et al. Reference Le Masson, Hatchuel and Weil2016). In the forcing protocol, however, the logic of generativity relies not only on the splitting knowledge structure but also on dense subsets. The present paper emphasized the issue of the splitting knowledge structure. However, this raises a complementary question: when building a splitting knowledge base, what are the consequences for the dense subsets? The generative filter that allows the generation of a new object is the intersection of the dense subsets of the initial set of objects. In the case presented here, the properties refining all properties of a potential new object are the constraints set by the architect; these constraints are indeed properties that each new façade or each new bookcase must absolutely satisfy in the eyes of the architect. In the bookcase sequence for instance, the dense subsets correspond to the stability, the respect of the firm identity and the possibility of integrating glass tiles. Since the generative effects of knowledge preordering come from the constitution of a splitting knowledge basis and the dense subsets, new objects could also come from a change in dense subsets. Further research is needed to understand how a change in dense subsets affects idea generation.
The above works have also prescriptive implications: they help identify a specific process of knowledge reorganization for generativity. This strategy of knowledge preordering has now been identified in communities such as those of artists, architects and engineers. Further research could further develop this process into new design methods and practices. Addressing explicitly the issue of knowledge and the knowledge structure, these methods could complement methods that tend to improve ideation. For instance, relying on the knowledge preordering for generativity, the evaluation and management of creativity sessions could be conducted with very different rules: (1) instead of focusing on the number of ideas generated, looking at the evolution of the knowledge structure and (2) targeting knowledge leading to knowledge preordering (i.e., leading to a change of rules in the initial knowledge space). Moreover, because of their special ability to combine several pieces of knowledge and concepts, non-verbal tools could precisely prove to be a privileged means of enhancing this generative structuration of knowledge during creativity sessions.
More generally, the lesson of the splitting condition is that design is about knowledge structures and the present paper has shown that sketching might be finally about evolving knowledge structures towards splitting structures, by sketching. We have observed this capacity for an experienced architect. One can wonder how to develop this capacity for novice architects. Even more, what could be the equivalent of ‘sketching for splitting knowledge’ for designers such as engineers and scientists?















