Article contents
X.—On the Economy of Heat in Expansive Machines, forming the Fifth Section of a Paper On the Mechanical Action of Heat
Published online by Cambridge University Press: 17 January 2013
Extract
(39.) A machine working by expansive power consists essentially of a portion of some substance to which heat is communicated, so as to expand it, at a higher temperature, being abstracted from it, so as to condense it to its original volume, at a lower temperature. The quantity of heat given out by the substance is less than the quantity received; the difference disappearing as heat to appear in the form of expansive power.
The heat originally received by the working body may act in two ways: to raise its temperature, and to expand it. The heat given out may also act in two ways: to lower the temperature, and to contract the body. Now, as the conversion of heat into expansive power arises from changes of volume only, and not from changes of temperature, it is obvious, that the proportion of the heat received which is converted into expansive power will be the greatest possible, when the reception of heat, and its emission, each take place at a constant temperature.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 20 , Issue 2 , 1853 , pp. 205 - 210
- Copyright
- Copyright © Royal Society of Edinburgh 1853
References
page 208 note * Prom information which I have received from Professor Thomson subsequently to the completion of this paper, it appears that his formula becomes identical with the approximate formula here proposed, on making the function called by him 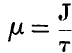 , J being Joule's equivalent.
, J being Joule's equivalent.
Mr Joule also, some time since, arrived at this approximate formula in the particular case of a perfect gas.
- 7
- Cited by


