Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T02:18:06.549Z Has data issue: false hasContentIssue false
  • English
  • Français

XV.—A New Method of Investigating Relations between Functions of the Roots of an Equation and its Coefficients

Published online by Cambridge University Press:  17 January 2013

J. Douglas Hamilton Dickson
J. Douglas Hamilton Dickson
Affiliation:
Fellow and Tutor of St Peter's College, Cambridge.
Get access Rights & Permissions [Opens in a new window]

Extract

I. If 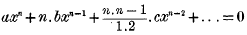be a rational equation of the nth degree, Newton's rule for a superior limit to the number of its imaginary roots depends upon the changes of sign in the series of functions—called, by Sylvester, Quadratic Elements—

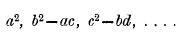
n + 1 in number.

It is a matter of some interest to know the relations in which the quadratic elements stand to the roots of the equation. The following method exhibits this relationship, and leads to others of a higher class.

Type
Research Article
Information
Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 29 , Issue 2 , 1880 , pp. 535 - 553
Copyright
Copyright © Royal Society of Edinburgh 1880

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 544 note * I have to thank Professor Cayley for valuable suggestions, in accordance with which the notation on the left hand sides of these equations was made to harmonise with that on the right hand sides. This will be seen more fully in the next section.

page 545 note * This is the ζ-function of Professor Sylvester.