Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T09:05:57.234Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlation Between Mesh Geometry and Stiffness Matrix Conditioning for Nonlocal Diffusion Models

Published online by Cambridge University Press:  16 July 2018

Jibum Kim
Jibum Kim*
Affiliation:
Department of Computer Science and Engineering, Incheon National University, Incheon, 406-772, South Korea.
*
*Corresponding author.Email address:jibumkim@incheon.ac.kr
Get access

Abstract

Nonlocal diffusion models involve integral equations that account for nonlocal interactions and do not explicitly employ differential operators in the space variables. Due to the nonlocality they might look different from classical partial differential equation (PDE) models, but their local limit reduces to partial differential equations. The effect of mesh element anisotropy mesh refinement and kernel functions on the conditioning of the stiffness matrix for a nonlocal diffusion model on 2D geometric domains is considered, and the results compared with those obtained from typical local PDE models. Numerical experiments show that the condition number is bounded by 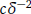(where c is a constant) for an integrable kernel function, and is not affected by the choice of the basis function. In contrast to local PDE models, mesh anisotropy and refinement affect the condition number very little.

Keywords

Peridynamicscondition numberfinite element method65R2065M60
Type
Research Article
Information
East Asian Journal on Applied Mathematics , Volume 4 , Issue 4 , November 2014 , pp. 312 - 328
Copyright
Copyright © Global-Science Press 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Silling, S.A., Reformulation of elasticity theory for discontinuities and long-range forces, J. Mech. Phys. Solids 48, 175–209 (2000).Google Scholar
[2] Bakunin, O.G., Turbulence and Diffusion: Scaling versus Equations, Springer Series in Synergetics, Springer (2008).Google Scholar
[3] Dagan, G., The significance of heterogeneity of evolving scales to transport in porous formations, Water Resources Res. 30, 3327–3336 (1994).Google Scholar
[4] Bobaru, F., Silling, S.A. and Jiang, H., Peridynamic fracture and damage modeling of membranes and nanofiber networks, in Proc. XI International Conference Fract., Turin, pp. 5748:1–6 (2005).Google Scholar
[5] Bobaru, F., Influence of van der Waals forces on increasing the strength and toughness in dynamic fracture of nanofiber networks: A peridynamic approach, Model. Simul. Mater. Sc. 15, 397–417 (2007).Google Scholar
[6] Emmrich, E., Lehoucq, R.B. and Puhst, D., Peridynamics: A nonlocal continuum theory, in Mesh-free Methods for Partial Differential Equations VI (2012).Google Scholar
[7] Silling, S.A. and Lehoucq, R.B., Peridynamic theory of solid mechanics, Adv. Appl. Mech. 44, 73–168 (2010).Google Scholar
[8] Silling, S.A. and Lehoucq, R.B., Convergence of peridynamics to classical elasticity theory, J. Elasticity 93, 13–37 (2008).CrossRefGoogle Scholar
[9] Du, Q., Kamm, J.R., Lehoucq, R. B. and Parks, M.L.. An approach to nonlocal, nonlinear advection, Technical report 2011-3164J, Sandia National Laboratories (2011).Google Scholar
[10] Aksoylu, B. and Parks, M., Variational theory and domain decomposition for nonlocal problems, Appl. Math. Comput. 217, 6498–6515 (2011).Google Scholar
[11] Macek, R.W. and Silling, S.A., Peridynamics via finite element analysis, Finite Elem. Anal. Des. 43, 1169–1178 (2007).Google Scholar
[12] Silling, S.A. and Askari, E., A meshfree method based on the peridynamic model of solid mechanics, Comput. Struct. 83, Advances in Meshfree Methods, 1526–1535 (2005).Google Scholar
[13] Chen, X. and Gunzburger, M., Continuous and discontinuous finite element methods for a peri-dynamic model of mechanics, Comput. Methods Appl. Mech. Eng. 200, 1237–1250 (2010).CrossRefGoogle Scholar
[14] Zhou, K. and Du, Q., Mathematical and numerical analysis of linear peridynamic models with nonlocal boundary conditions, SIAM J. Numer. Anal. 48, 1759–1780 (2010).Google Scholar
[15] Du, Q., Wang, D. and Zhu, L., On mesh geometry and stiffness matrix conditioning for general finite element spaces, SIAM J. Numer. Anal. 47, 1421–1444 (2009).Google Scholar
[16] Shewchuk, J., What is a Good Linear Finite Element? Interpolation, Conditioning, Anisotropy and Quality Measures, Technical Report, Department of Computer Science, University of California, Berkeley (2003).Google Scholar
[17] Kim, J., Sastry, S.P. and Shontz, S.M., Efficient solution of elliptic partial differential equations via effective combination of mesh quality metrics, preconditioners, and sparse linear solvers, Proc. 19th International Meshing Roundtable Conference, pp. 103–120, Chattanooga (2010).Google Scholar
[18] Kim, J., Sastry, S.P. and Shontz, S.M., A numerical investigation on the interplay among geometry, meshes, and linear algebra in the finite element solution of elliptic PDE, Eng. Comput. 28, 431–450 (2012).Google Scholar
[19] Silling, S., Epton, M., Weckner, O., Xu, J. and Askari, E., Peridynamic states and constitutive modeling, J. Elast. 88, 151–184 (2007).Google Scholar
[20] Kebing, Y., Xin, X.J. and Lease, K.B., A new method of adaptive integration with error control for bond-based peridynamics, in Proc. of the World Congress on Engineering and Computer Science, San Francisco (2010).Google Scholar
[21] Burkardt, J., Quadrature rules for triangles, http://people.sc.fsu.edu/∼jburkardt.Google Scholar
[22] Picasso, M., Adaptive finite elements with large aspect ratio based on an anisotropic error estimator involving first order derivatives, Comput. Method Appl. Math. 196, 14–23 (2006).Google Scholar