Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T01:03:17.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Features of the Nyström Method for the Sherman-Lauricella Equation on Piecewise Smooth Contours

Published online by Cambridge University Press:  28 May 2015

Victor D. Didenko  and
Johan Heising
Victor D. Didenko*
Affiliation:
Faculty of Science, University of Brunei Darussalam, Bandar Seri Begawan, BE1410 Brunei
Johan Heising*
Affiliation:
Numerical Analysis, Centre for Mathematical Sciences, Lund University, Box 118, SE-221 00 Lund, Sweden
*
Corresponding author. Email: diviol@gmail.com
Corresponding author. Email: helsing@maths.lth.se
Get access

Abstract

The stability of the Nyström method for the Sherman-Lauricella equation on contours with corner points cj, j = 0, 1, …, m relies on the invertibility of certain operators 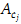belonging to an algebra of Toeplitz operators. The operators 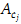do not depend on the shape of the contour, but on the opening angle θj of the corresponding corner cj and on parameters of the approximation method mentioned. They have a complicated structure and there is no analytic tool to verify their invertibility. To study this problem, the original Nyström method is applied to the Sherman-Lauricella equation on a special model contour that has only one corner point with varying opening angle In the interval (0.1π, 1.9π), it is found that there are 8 values of θj where the invertibility of the operator 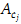may fail, so the corresponding original Nyström method on any contour with corner points of such magnitude cannot be stable and requires modification.

Keywords

65R2045L05Sherman-Lauricella equationNyström methodstability
Type
Review Article
Information
East Asian Journal on Applied Mathematics , Volume 1 , Issue 4 , November 2011 , pp. 403 - 414
Copyright
Copyright © Global-Science Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Atkinson, K. E., The Numerical Solution of Integral Equations of the Second Kind, Cambridge University Press, Cambridge, 1997.CrossRefGoogle Scholar
[2]Crowdy, D., Exact solutions for the viscous sintering of multiply-connected fluid domains, J. Engrg. Math., 42 (2002), pp. 225–242.Google Scholar
[3]Didenko, V. D. and Helsing, J., Stability of the Nyström method for the Sherman-Lauricella equation, SIAM J. Numer. Anal., 49 (2011), pp. 1127–1148.CrossRefGoogle Scholar
[4]Didenko, V. D., Roch, S. and Silbermann, B., Approximation methods for singular integral equations with conjugation on curves with corners, SIAM J. Numer. Anal., 32 (1995), pp. 1910–1939.Google Scholar
[5]Didenko, V. D. and Silbermann, B., Stability of approximation methods on locally non-equidistant meshes for singular integral equations. J. Integral Equations Appl., 11 (1999), pp. 54–87.CrossRefGoogle Scholar
[6]Didenko, V. D. and Silbermann, B., On stability of approximation methods for the Muskhelishvili equation, J. Comp. Appl. Math., 146/2 (2002), pp. 419–441.Google Scholar
[7]Didenko, V. D. and Silbermann, B., Approximation af Additive Convolution-Like Operators. Real C*-Algebra Approach, Front. Math., Birkhäuser, Basel, 2008.Google Scholar
[8]Helsing, J., On the interior stress problem for elastic bodies. ASME J. Appl. Mech., 67 (2000), pp. 658–662.CrossRefGoogle Scholar
[9]Helsing, J. and Ojala, R., Corner singularities for elliptic problems: Integral equations, graded meshes, quadrature, and compressed inverse preconditioning, J. Comput. Phys., 227 (2008), pp. 8820–8840.Google Scholar
[10]Helsing, J., A fast and stable solver for singular integral equations on piecewise smooth curves, SIAM J. Sci. Comput., 33 (2011), pp. 153–174.Google Scholar
[11]Mikhlin, S. G., Integral Equations and Their Applications to Certain Problems in Mechanics, Mathematical Physics and Technology, 2nd ed., Pergamon Press, London, 1964.Google Scholar
[12]Muskhelishvili, N. I., Fundamental Problems in the Theory of Elasticity, Nauka, Moscow, 1966.Google Scholar
[13]Muskhelishvili, N. I., Singular Integral Equations, Nauka, Moscow, 1968Google Scholar
[14]Parton, V. Z. and Perlin, P. I., Integral Equations of Elasticity, MIR, Moscow, 1982.Google Scholar