Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:30:33.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Lubich Second-Order Methods for Distributed-Order Time-Fractional Differential Equations with Smooth Solutions

Published online by Cambridge University Press:  12 May 2016

Rui Du ,
Zhao-peng Hao  and
Zhi-zhong Sun
Rui Du*
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, China
Zhao-peng Hao
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, China
Zhi-zhong Sun
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210096, China
*
*Corresponding author. Email addresses:rdu@seu.edu.cn (R. Du), haochpeng@126.com (Z. Hao), zzsun@seu.edu.cn (Z. Sun)
Get access

Abstract

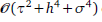This article is devoted to the study of some high-order difference schemes for the distributed-order time-fractional equations in both one and two space dimensions. Based on the composite Simpson formula and Lubich second-order operator, a difference scheme is constructed with convergence in the L1(L∞)-norm for the one-dimensional case, where τ,h and σ are the respective step sizes in time, space and distributed-order. Unconditional stability and convergence are proven. An ADI difference scheme is also derived for the two-dimensional case, and proven to be unconditionally stable and 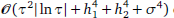convergent in the L1(L∞)-norm, where h1 and h2 are the spatial step sizes. Some numerical examples are also given to demonstrate our theoretical results.

Keywords

Distributed-order time-fractional equationsLubich operatorcompact difference schemeADI schemeconvergencestability
Type
Research Article
Information
East Asian Journal on Applied Mathematics , Volume 6 , Issue 2 , May 2016 , pp. 131 - 151
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Podlubny,, I.Fractional Differential Equations, Academic Press, New York (1999).Google Scholar
[2]Oldham, K.B. and Spanier, J., The Fractional Calculus, Academic Press, New York (1974).Google Scholar
[3]Kilbas, A., Srivastava, H. and Trujillo, J., Theory and Applications of Fractional Differential Equations, Elsevier, Boston (2006).Google Scholar
[4]Mainardi, F., Fractional Calculus and Waves in Linear Viscoelasticity, Imperial College Press, London (2010).CrossRefGoogle Scholar
[5]Huang, F. and Liu, F., The time fractional diffusion equation and the advection-dispersion equation, ANZIAM J. 46, 317–330 (2005).CrossRefGoogle Scholar
[6]Gorenflo, R., Luchko, Y.and Mainardi, F.Wright functions as scale-invariant solutions of the diffusion-wave equation, J. Comp. Appl. Math. 118, 175–191 (2000).CrossRefGoogle Scholar
[7]Povstenko, Y., Non-central-symmetric solution to time-fractional diffusion-wave equation in a sphere under Dirichlet boundary condition, Fract. Calc. Appl. Anal. 15, 253–266 (2012).CrossRefGoogle Scholar
[8]Ray, S.S. and Bera, R.K., Analytical solution of a fractional diffusion equation by Adomian decomposition method, Appl. Math. Comp. 174, 329–336 (2006).Google Scholar
[9]Yuste, S. and Acedo, L., An explicit finite difference method and a new von Neumann-type stability analysis for fractional diffusion equations, SIAM J. Num. Anal. 42, 1862–1874 (2005).CrossRefGoogle Scholar
[10]Langlands, T. and Henry, B., The accuracy and stability of an implicit solution method for the fractional diffusion equation, J. Comp. Phys. 205, 719–736 (2005).CrossRefGoogle Scholar
[11]Chen, C., Liu, F., Turner, I. and Anh, V., A Fourier method for the fractional diffusion equation describing sub-diffusion, J. Comp. Phys. 227, 886–897 (2007).CrossRefGoogle Scholar
[12]Zhuang, P., Liu, F., Anh, V. and Turner, I., New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation, SIAM J. Num. Anal. 46, 1079–1095 (2008).CrossRefGoogle Scholar
[13]Cao, J. and Xu, C., A high order schema for the numerical solution of the fractional ordinary differential equations, J. Comp. Phys. 238, 154–168 (2013).CrossRefGoogle Scholar
[14]Li, C. and Ding, H., Higher order finite difference method for the reaction and anomalous-diffusion equation, Appl. Math. Model. 38, 3802–3821 (2014).CrossRefGoogle Scholar
[15]Sun, Z.Z. and Wu, X., A fully discrete difference scheme for a diffusion-wave system, Appl. Num. Math. 56, 193–209 (2006).CrossRefGoogle Scholar
[16]Wang, Z. and Vong, S., Compact difference schemes for the modified anomalous fractional subdiffusion equation and the fractional diffusion-wave equation, J. Comp. Phys. 277, 1–15 (2014).CrossRefGoogle Scholar
[17]Li, C. and Zeng, F., Finite difference methods for fractional differential equations, Int. J. Bifurcation Chaos 22(04), 1230014 (2012).CrossRefGoogle Scholar
[18]Cui, M., Compact alternating direction implicit method for two-dimensional time fractional diffusion equation, J. Comp. Phys. 231, 2621–2633 (2012).CrossRefGoogle Scholar
[19]Cui, M., Convergence analysis of high-order compact alternating direction implicit schemes for the two-dimensional time fractional diffusion equation, Num. Algor. 62, 383–409 (2013).CrossRefGoogle Scholar
[20]Zhang, Y.N. and Sun, Z.Z., Alternating direction implicit schemes for the two-dimensional fractional subdiffusion equation, J. Comp. Phys. 230, 8713–8728 (2011).CrossRefGoogle Scholar
[21]Zhang, Y.N. and Sun, Z.Z., Error analysis of a compact ADI scheme for the 2D fractional subdiffusion equation, J. Sci. Comp. 59, 104–128 (2014).CrossRefGoogle Scholar
[22]Dimitrov, Y., Numerical approximations for fractional differential equations, J. Fract. Calc. Appl. 5, suppl. 3S, No. 22, 45 pp. (2014).Google Scholar
[23]Podlubny, I., Skovranek, T., Jara, B.M., Petras, J., Verbitsky, V. and Chen, Y.Q., Matrix approach to discrete fractional calculus III: Non-equidistant grids, variable step length and distributed orders, Phil. Trans. R. Soc. A 371, 20120153 (2012).Google Scholar
[24]Diethelm, K. and Ford, N.J., Numerical analysis for distributed order differential equations, J. Comp. Appl. Math. 225, 96–104 (2009).CrossRefGoogle Scholar
[25]Liu, F., Meerschaert, M.M., McGough, R.J., Zhuang, P. and Liu, Q., Numerical methods for solving the multi-term time-fractional wave-diffusion equation, Fract. Calc. Appl. Anal. 16, 9–25 (2013).CrossRefGoogle ScholarPubMed
[26]Ye, H., Liu, F., Anh, V. and Turner, I., Numerical analysis for the time distributed-order and Riesz space fractional diffusions on bounded domains, IMA J. Appl. Math. 80, 825–838 (2015).CrossRefGoogle Scholar
[27]Ford, N.J., Morgado, M.L. and Rebelo, M., A numerical method for the distributed order time-fractional diffusion equation, ICFDA'14 Catania, ISBN 978-1-4799-2590-2, pp. 23–25 (2014).Google Scholar
[28]Morgado, M.L. and Rebelo, M., Numerical approximation of distributed order reaction-diffusion equations, J. Comp. Appl. Math. 275, 216–227 (2014).CrossRefGoogle Scholar
[29]Katsikadelis, J.T., Numerical solution of distributed order fractional differential equations, J. Comp. Phys. 259, 11–22 (2014).CrossRefGoogle Scholar
[30]Lubich, C., Discretizedfractional calculus, SIAM J. Math. Anal. 17, 704–719 (1986).CrossRefGoogle Scholar
[31]Brunner, H. and Van der Houwen, P.J., The Numerical Solution of Volterra Equations, CWI Monographs, Vol. 3. North-Holland, Amsterdam, (1986).Google Scholar
[32]Zhou, H., Tian, W.Y. and Deng, W., Quasi-compact finite difference schemes for space fractional diffusion equations, J. Sci. Comp. 56, 45–66 (2013).CrossRefGoogle Scholar
[33]Sun, Z.Z., Numerical Methods of Partial Differential Equations, Science Press, Beijing (2012).Google Scholar
[34]Liao, H.L. and Sun, Z.Z., Maximum norm error bounds of ADI and compact ADI methods for solving parabolic equations, Num. Meth. Partial Differential Eq. 26, 37–60 (2010).CrossRefGoogle Scholar
[35]Henrici, P., Fast Fourier methods in computational complex analysis, SIAM Rev. 21, 481–527 (1979).CrossRefGoogle Scholar