Article contents
AVERAGE DERIVATIVE ESTIMATION UNDER MEASUREMENT ERROR
Published online by Cambridge University Press: 13 November 2020
Abstract
In this paper, we derive the asymptotic properties of the density-weighted average derivative estimator when a regressor is contaminated with classical measurement error and the density of this error must be estimated. Average derivatives of conditional mean functions are used extensively in economics and statistics, most notably in semiparametric index models. As well as ordinary smooth measurement error, we provide results for supersmooth error distributions. This is a particularly important class of error distribution as it includes the Gaussian density. We show that under either type of measurement error, despite using nonparametric deconvolution techniques and an estimated error characteristic function, we are able to achieve a 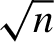 $\sqrt {n}$-rate of convergence for the average derivative estimator. Interestingly, if the measurement error density is symmetric, the asymptotic variance of the average derivative estimator is the same irrespective of whether the error density is estimated or not. The promising finite sample performance of the estimator is shown through a Monte Carlo simulation.
$\sqrt {n}$-rate of convergence for the average derivative estimator. Interestingly, if the measurement error density is symmetric, the asymptotic variance of the average derivative estimator is the same irrespective of whether the error density is estimated or not. The promising finite sample performance of the estimator is shown through a Monte Carlo simulation.
Information
- Type
- ARTICLES
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Financial support from the ERC Consolidator Grant (SNP 615882) (Otsu) and the AUFF Starting Grant (26852) (Taylor) is gratefully acknowledged.
References
REFERENCES
- 2
- Cited by

