Article contents
ESTIMATORS FOR PERSISTENT AND POSSIBLY NONSTATIONARY DATA WITH CLASSICAL PROPERTIES
Published online by Cambridge University Press: 27 April 2012
Abstract
This paper considers a moments-based nonlinear estimator that is 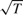 $\root\of T $-consistent and uniformly asymptotically normal irrespective of the degree of persistence of the forcing process. These properties hold for linear autoregressive models, linear predictive regressions, and certain nonlinear dynamic models. Asymptotic normality is obtained because the moments are chosen so that the objective function is uniformly bounded in probability and so that a central limit theorem can be applied. Critical values from the normal distribution can be used irrespective of the treatment of the deterministic terms. Simulations show that the estimates are precise and the t-test has good size in the parameter region where the least squares estimates usually yield distorted inference.
$\root\of T $-consistent and uniformly asymptotically normal irrespective of the degree of persistence of the forcing process. These properties hold for linear autoregressive models, linear predictive regressions, and certain nonlinear dynamic models. Asymptotic normality is obtained because the moments are chosen so that the objective function is uniformly bounded in probability and so that a central limit theorem can be applied. Critical values from the normal distribution can be used irrespective of the treatment of the deterministic terms. Simulations show that the estimates are precise and the t-test has good size in the parameter region where the least squares estimates usually yield distorted inference.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
REFERENCES
- 9
- Cited by

