Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Phillips, Peter C. B.
2008.
The New Palgrave Dictionary of Economics.
p.
1.
Chen, Jhih-Gang
and
Kuo, Biing-Shen
2009.
Gaussian Inference in General AR(1) Models Based on Long Difference.
SSRN Electronic Journal,
Kruiniger, Hugo
2009.
GMM ESTIMATION AND INFERENCE IN DYNAMIC PANEL DATA MODELS WITH PERSISTENT DATA.
Econometric Theory,
Vol. 25,
Issue. 5,
p.
1348.
Han, Chirok
and
Phillips, Peter C. B.
2010.
GMM ESTIMATION FOR DYNAMIC PANELS WITH FIXED EFFECTS AND STRONG INSTRUMENTS AT UNITY.
Econometric Theory,
Vol. 26,
Issue. 1,
p.
119.
Phillips, Peter C. B.
2010.
Macroeconometrics and Time Series Analysis.
p.
347.
Han, Chirok
Phillips, Peter C. B.
and
Sul, Donggyu
2010.
X-Differencing and Dynamic Panel Model Estimation.
SSRN Electronic Journal,
Han, Chirok
Phillips, Peter C. B.
and
Sul, Donggyu
2010.
Uniform Asymptotic Normality in Stationary and Unit Root Autoregression.
SSRN Electronic Journal,
Han, Chirok
Phillips, Peter C. B.
and
Sul, Donggyu
2011.
UNIFORM ASYMPTOTIC NORMALITY IN STATIONARY AND UNIT ROOT AUTOREGRESSION.
Econometric Theory,
Vol. 27,
Issue. 6,
p.
1117.
Camponovo, Lorenzo
2012.
Differencing Transformations and Robust Inference in Predictive Regression Models.
SSRN Electronic Journal,
Nagata, Shuichi
2012.
Edgeworth Approximation of a Finite Sample Distribution for an AR(1) Model with Measurement Error.
Open Journal of Statistics,
Vol. 02,
Issue. 04,
p.
383.
Gorodnichenko, Yuriy
Mikusheva, Anna
and
Ng, Serena
2012.
ESTIMATORS FOR PERSISTENT AND POSSIBLY NONSTATIONARY DATA WITH CLASSICAL PROPERTIES.
Econometric Theory,
Vol. 28,
Issue. 5,
p.
1003.
Chen, Jhih‐Gang
and
Kuo, Biing‐Shen
2013.
Gaussian inference in general AR(1) models based on difference.
Journal of Time Series Analysis,
Vol. 34,
Issue. 4,
p.
447.
Phillips, Peter C. B.
and
Han, Chirok
2014.
True Limit Distributions of the Anderson-Hsiao Iv Estimators in Panel Autoregression.
SSRN Electronic Journal,
Han, Chirok
Phillips, Peter C. B.
and
Sul, Donggyu
2014.
X-DIFFERENCING AND DYNAMIC PANEL MODEL ESTIMATION.
Econometric Theory,
Vol. 30,
Issue. 1,
p.
201.
Phillips, Peter C.B.
and
Han, Chirok
2015.
The true limit distributions of the Anderson–Hsiao IV estimators in panel autoregression.
Economics Letters,
Vol. 127,
Issue. ,
p.
89.
Camponovo, Lorenzo
2015.
DIFFERENCING TRANSFORMATIONS AND INFERENCE IN PREDICTIVE REGRESSION MODELS.
Econometric Theory,
Vol. 31,
Issue. 6,
p.
1331.
Phillips, Peter C. B.
2018.
The New Palgrave Dictionary of Economics.
p.
14061.
Zhou, Hui
and
Li, Jie
2018.
Empirical likelihood inference for error density estimators in first-order autoregression models.
Communications in Statistics - Theory and Methods,
Vol. 47,
Issue. 10,
p.
2351.
Das, Panchanan
2019.
Econometrics in Theory and Practice.
p.
541.
Müller, Ulrich K.
and
Wang, Yulong
2019.
Nearly weighted risk minimal unbiased estimation.
Journal of Econometrics,
Vol. 209,
Issue. 1,
p.
18.

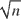 rate of convergence. En route, a useful central limit theorem (CLT) for sample covariances of linear processes is given, following Phillips and Solo (1992,
rate of convergence. En route, a useful central limit theorem (CLT) for sample covariances of linear processes is given, following Phillips and Solo (1992, 