Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Veraart, Almut E. D.
2011.
How precise is the finite sample approximation of the asymptotic distribution of realised variation measures in the presence of jumps?.
AStA Advances in Statistical Analysis,
Vol. 95,
Issue. 3,
p.
253.
Bandi, Federico M.
and
Renò, Roberto
2012.
Time-varying leverage effects.
Journal of Econometrics,
Vol. 169,
Issue. 1,
p.
94.
2012.
Handbook of Volatility Models and Their Applications.
p.
487.
Jing, Bing-Yi
Li, Cui-Xia
and
Liu, Zhi
2013.
On Estimating the Integrated Co-Volatility Using Noisy High-Frequency Data with Jumps.
Communications in Statistics - Theory and Methods,
Vol. 42,
Issue. 21,
p.
3889.
Varneskov, Rasmus
and
Voev, Valeri
2013.
The role of realized ex-post covariance measures and dynamic model choice on the quality of covariance forecasts.
Journal of Empirical Finance,
Vol. 20,
Issue. ,
p.
83.
Koike, Yuta
2013.
Estimation of Integrated Covariances in the Simultaneous Presence of Nonsynchronicity, Microstructure Noise and Jumps.
SSRN Electronic Journal,
Gnabo, Jean-Yves
Hvozdyk, Lyudmyla
and
Lahaye, Jérôme
2014.
System-wide tail comovements: A bootstrap test for cojump identification on the S&P 500, US bonds and currencies.
Journal of International Money and Finance,
Vol. 48,
Issue. ,
p.
147.
Koike, Yuta
2014.
An estimator for the cumulative co‐volatility of asynchronously observed semimartingales with jumps.
Scandinavian Journal of Statistics,
Vol. 41,
Issue. 2,
p.
460.
Vander Elst, Harry
and
Veredas, David
2014.
Disentangled Jump-Robust Realized Covariances and Correlations with Non-Synchronous Prices.
SSRN Electronic Journal,
Caporin, Massimiliano
Kolokolov, Alexey
and
Renn, Roberto
2014.
Multi-Jumps.
SSRN Electronic Journal,
Gnabo, Jean-Yves
Hvozdyk, Liudmyla
and
Lahaye, JJrrme
2014.
System-Wide Tail Comovements: A Bootstrap Test for Cojump Identification on the S&P 500, US Bonds and Exchange Rates.
SSRN Electronic Journal,
Djellout, Hacène
and
Samoura, Yacouba
2014.
Large and moderate deviations of realized covolatility.
Statistics & Probability Letters,
Vol. 86,
Issue. ,
p.
30.
Huth, Nicolas
and
Abergel, Frédéric
2014.
High frequency lead/lag relationships — Empirical facts.
Journal of Empirical Finance,
Vol. 26,
Issue. ,
p.
41.
Ubukata, Masato
and
Watanabe, Toshiaki
2015.
Evaluating the performance of futures hedging using multivariate realized volatility.
Journal of the Japanese and International Economies,
Vol. 38,
Issue. ,
p.
148.
Bibinger, Markus
and
Winkelmann, Lars
2015.
Econometrics of co-jumps in high-frequency data with noise.
Journal of Econometrics,
Vol. 184,
Issue. 2,
p.
361.
Reiß, Markus
Todorov, Viktor
and
Tauchen, George
2015.
Nonparametric test for a constant beta between Itô semi-martingales based on high-frequency data.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 8,
p.
2955.
Mancini, Cecilia
2015.
Truncated Realized Covariance When Prices Have Infinite Variation Jumps.
SSRN Electronic Journal,
Christensen, Kim
and
Hounyo, Ulrich
2016.
Testing for Heteroscedasticity in Jumpy and Noisy High-frequency Data: A Resampling Approach.
SSRN Electronic Journal,
Varneskov, Rasmus Tangsgaard
2016.
Flat-Top Realized Kernel Estimation of Quadratic Covariation With Nonsynchronous and Noisy Asset Prices.
Journal of Business & Economic Statistics,
Vol. 34,
Issue. 1,
p.
1.
Koike, Yuta
2016.
ESTIMATION OF INTEGRATED COVARIANCES IN THE SIMULTANEOUS PRESENCE OF NONSYNCHRONICITY, MICROSTRUCTURE NOISE AND JUMPS.
Econometric Theory,
Vol. 32,
Issue. 3,
p.
533.
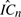 is used, which substantially excludes from RC all terms containing jumps. Unlike in Jacod (2007, Universite de Paris-6) and Jacod (2008, Stochastic Processes and Their Applications 118, 517–559), no assumptions on the volatilities’ dynamics are required. In the presence of only finite activity jumps: 1) central limit theorems (CLTs) for
is used, which substantially excludes from RC all terms containing jumps. Unlike in Jacod (2007, Universite de Paris-6) and Jacod (2008, Stochastic Processes and Their Applications 118, 517–559), no assumptions on the volatilities’ dynamics are required. In the presence of only finite activity jumps: 1) central limit theorems (CLTs) for 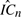 and for further measures of dependence between the two Brownian parts are obtained; the estimation error asymptotic variance is shown to be smaller than for the alternative estimators of IC in the literature; 2) by also selecting the observations as in Hayashi and Yoshida (2005, Bernoulli 11, 359–379), robustness to nonsynchronous data is obtained. The proposed estimators are shown to have good finite sample performances in Monte Carlo simulations even with an observation frequency low enough to make microstructure noises’ impact on data negligible.
and for further measures of dependence between the two Brownian parts are obtained; the estimation error asymptotic variance is shown to be smaller than for the alternative estimators of IC in the literature; 2) by also selecting the observations as in Hayashi and Yoshida (2005, Bernoulli 11, 359–379), robustness to nonsynchronous data is obtained. The proposed estimators are shown to have good finite sample performances in Monte Carlo simulations even with an observation frequency low enough to make microstructure noises’ impact on data negligible.
