Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kan, Kamhon
and
Kao, Chihwa D.
2005.
Simulation-Based Two-Step Estimation with Endogenous Regressors.
SSRN Electronic Journal,
Tang, Xun
2009.
Binary Regressions with Bounded Median Dependence.
SSRN Electronic Journal,
Song, Kyungchul
2009.
Two-Step Extremum Estimation with Estimated Single-Indices.
SSRN Electronic Journal,
De Luca, Giuseppe
and
Perotti, Valeria
2010.
Estimation of Ordered Response Models with Sample Selection.
SSRN Electronic Journal,
Muendler, Marc-Andreas
and
Becker, Sascha O
2010.
Margins of Multinational Labor Substitution.
American Economic Review,
Vol. 100,
Issue. 5,
p.
1999.
Song, Kyungchul
2010.
Bootstrapping Semiparametric Models with Single-Index Nuisance Parameters, Second Version.
SSRN Electronic Journal,
Chen, Songnian
and
Zhou, Yahong
2010.
Semiparametric and nonparametric estimation of sample selection models under symmetry.
Journal of Econometrics,
Vol. 157,
Issue. 1,
p.
143.
De Luca, Giuseppe
and
Perotti, Valeria
2011.
Estimation of Ordered Response Models with Sample Selection.
The Stata Journal: Promoting communications on statistics and Stata,
Vol. 11,
Issue. 2,
p.
213.
Huber, Martin
and
Melly, Blaise
2012.
A Test of the Conditional Independence Assumption In Sample Selection Models.
SSRN Electronic Journal,
Song, Kyungchul
2014.
Semiparametric models with single-index nuisance parameters.
Journal of Econometrics,
Vol. 178,
Issue. ,
p.
471.
Chen, Stacey H.
and
Khan, Shakeeb
2014.
SEMI-PARAMETRIC ESTIMATION OF PROGRAM IMPACTS ON DISPERSION OF POTENTIAL WAGES.
Journal of Applied Econometrics,
Vol. 29,
Issue. 6,
p.
901.
Huber, Martin
and
Melly, Blaise
2015.
A Test of the Conditional Independence Assumption in Sample Selection Models.
Journal of Applied Econometrics,
Vol. 30,
Issue. 7,
p.
1144.
Santos Silva, J. M. C.
and
Tenreyro, Silvana
2015.
Trading Partners and Trading Volumes: Implementing the Helpman–Melitz–Rubinstein Model Empirically.
Oxford Bulletin of Economics and Statistics,
Vol. 77,
Issue. 1,
p.
93.
Krishnamurthy, Chandra Kiran B.
and
Kriström, Bengt
2016.
Determinants of the Price-Premium for Green Energy: Evidence from an OECD Cross-Section.
Environmental and Resource Economics,
Vol. 64,
Issue. 2,
p.
173.
Milunovich, George
and
Yang, Minxian
2018.
Simultaneous Equation Systems With Heteroscedasticity: Identification, Estimation, and Stock Price Elasticities.
Journal of Business & Economic Statistics,
Vol. 36,
Issue. 2,
p.
288.
Mu, Beili
and
Zhang, Zhengyu
2018.
Identification and estimation of heteroscedastic binary choice models with endogenous dummy regressors.
The Econometrics Journal,
Vol. 21,
Issue. 2,
p.
218.
D’Haultfœuille, Xavier
Maurel, Arnaud
and
Zhang, Yichong
2018.
Extremal quantile regressions for selection models and the black–white wage gap.
Journal of Econometrics,
Vol. 203,
Issue. 1,
p.
129.
Biewen, Martin
Fitzenberger, Bernd
and
Seckler, Matthias
2020.
Counterfactual quantile decompositions with selection correction taking into account Huber/Melly (2015): An application to the German gender wage gap.
Labour Economics,
Vol. 67,
Issue. ,
p.
101927.
D’Haultfœuille, Xavier
Maurel, Arnaud
Qiu, Xiaoyun
and
Zhang, Yichong
2020.
Estimating selection models without an instrument with Stata.
The Stata Journal: Promoting communications on statistics and Stata,
Vol. 20,
Issue. 2,
p.
297.
Biewen, Martin
and
Erhardt, Pascal
2021.
arhomme: An implementation of the Arellano and Bonhomme (2017) estimator for quantile regression with selection correction.
The Stata Journal: Promoting communications on statistics and Stata,
Vol. 21,
Issue. 3,
p.
602.
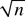 -consistent and asymptotically normal, and the form of its limiting covariance matrix is derived.We are grateful to B. Honoré, R. Klein, E. Kyriazidou, L.-F. Lee, J. Powell, two anonymous referees, and the co-editor D. Andrews and also to seminar participants at Princeton, Queens, UCLA, and the University of Toronto for helpful comments. Chen's research was supported by RGC grant HKUST 6070/01H from the Research Grants Council of Hong Kong.
-consistent and asymptotically normal, and the form of its limiting covariance matrix is derived.We are grateful to B. Honoré, R. Klein, E. Kyriazidou, L.-F. Lee, J. Powell, two anonymous referees, and the co-editor D. Andrews and also to seminar participants at Princeton, Queens, UCLA, and the University of Toronto for helpful comments. Chen's research was supported by RGC grant HKUST 6070/01H from the Research Grants Council of Hong Kong.
