Article contents
TESTING GENERALIZED REGRESSION MONOTONICITY
Published online by Cambridge University Press: 18 December 2018
Abstract
We propose a test for a generalized regression monotonicity (GRM) hypothesis. The GRM hypothesis is the sharp testable implication of the monotonicity of certain latent structures, as we show in this article. Examples include the monotonicity of the conditional mean function when only interval data are available for the dependent variable and the monotone instrumental variable assumption of Manski and Pepper (2000). These instances of latent monotonicity can be tested using our test. Moreover, the GRM hypothesis includes regression monotonicity and stochastic monotonicity as special cases. Thus, our test also serves as an alternative to existing tests for those hypotheses. We show that our test controls the size uniformly over a broad set of data generating processes asymptotically, is consistent against fixed alternatives, and has nontrivial power against some 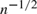 ${n^{ - 1/2}}$ local alternatives.
${n^{ - 1/2}}$ local alternatives.
Information
- Type
- ARTICLES
- Information
- Copyright
- Copyright © Cambridge University Press 2018
Footnotes
Yu-Chin Hsu gratefully acknowledges the research support from Ministry of Science and Technology of Taiwan (MOST103-2628-H-001-001-MY4 and MOST107-2410-H-001 -034 -MY3) and Career Development Award of Academia Sinica, Taiwan. All errors and omissions are our own responsibility.
References
REFERENCES
- 17
- Cited by

