Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T19:46:15.108Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTICS FOR TIME-VARYING VECTOR MA(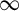$\infty $) PROCESSES

Published online by Cambridge University Press:  09 January 2024

Yayi Yan ,
Jiti Gao Open the ORCID record for Jiti Gao [Opens in a new window]  and
Bin Peng Open the ORCID record for Bin Peng [Opens in a new window]
Yayi Yan
Affiliation:
Shanghai University of Finance and Economics and Monash University
Jiti Gao*
Affiliation:
Monash University
Bin Peng
Affiliation:
Monash University
*
Address correspondence to Jiti Gao, Department of Econometrics and Business Statistics, Monash University, Caulfield East, VIC 3145, Australia; e-mail: Jiti.Gao@monash.edu.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper introduces a new class of time-varying vector moving average processes of infinite order. These processes serve dual purposes: (1) they can be used to model time-varying dependence structures, and (2) they can be used to establish asymptotic theories for multivariate time series models. To illustrate these two points, we first establish some fundamental asymptotic properties and use them to infer the trending term of a vector moving average infinity process. We then investigate a class of time-varying VARX models. Finally, we demonstrate the empirical relevance of the theoretical results using extensive simulated and real data studies.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 33
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Footnotes

The authors of this paper would like to thank the Co-Editor, Yixiao Sun, and two referees for their constructive comments. Thanks also go to George Athanasopoulos, Rainer Dahlhaus, David Frazier, Oliver Linton, Gael Martin, Peter C. B. Phillips, and Wei Biao Wu for their helpful comments on earlier versions of this paper. Yan acknowledges the financial support of the National Natural Science Foundation of China (Grant No. 72303142) and Fundamental Research Funds for the Central Universities (Grant Nos. 2022110877 & 2023110099). Both Gao and Peng acknowledge the Australian Research Council Discovery Grants Program for its financial support under Grant Numbers: DP200102769 and DP210100476.

References

Andrews, D. W. (1991). Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica, 59(3), 817–858.CrossRefGoogle Scholar
Beveridge, S., & Nelson, C. R. (1981). A new approach to decomposition of economic time series into permanent and transitory components with particular attention to measurement of the business cycle. Journal of Monetary Economics, 7(2), 151–174.CrossRefGoogle Scholar
Bhattacharya, R. N., & Rao, R. R. (1986). Normal approximation and asymptotic expansions. SIAM.Google Scholar
Billingsley, P. (2013). Convergence of probability measures. John Wiley & Sons.Google Scholar
Brüggemann, R., Jentsch, C., & Trenkler, C. (2016). Inference in VARs with conditional heteroskedasticity of unknown form. Journal of Econometrics, 191(1), 69–85.CrossRefGoogle Scholar
Bühlmann, P. (1998). Sieve bootstrap for smoothing in nonstationary time series. Annals of Statistics, 26(1), 48–83.CrossRefGoogle Scholar
Casini, A. (2023). Theory of evolutionary spectra for heteroskedasticity and autocorrelation robust inference in possibly misspecified and nonstationary models. Journal of Econometrics, 235(2), 372–392.CrossRefGoogle Scholar
Chu, C.-K., & Marron, J. S. (1991). Comparison of two bandwidth selectors with dependent errors. Annals of Statistics, 19(4), 1906–1918.CrossRefGoogle Scholar
Cogley, T., Primiceri, G. E., & Sargent, T. J. (2010). Inflation-gap persistence in the U.S. American Economic Journal: Macroeconomics, 2(1), 43–69.Google Scholar
Dahlhaus, R. (2012). Locally stationary processes. In T. Subba Rao, S. Subba Rao & C.R. Rao (eds.), Handbook of statistics, vol. 30 (pp. 351–413). Elsevier.Google Scholar
Dahlhaus, R., & Polonik, W. (2009). Empirical spectral processes for locally stationary time series. Bernoulli, 15(1), 1–39.CrossRefGoogle Scholar
Dahlhaus, R., & Rao, S. S. (2006). Statistical inference for time-varying ARCH processes. Annals of Statistics, 34(3), 1075–1114.CrossRefGoogle Scholar
Doukhan, P. (2012). Mixing: Properties and examples, vol. 85. Springer Science & Business Media.Google Scholar
Fan, J., & Huang, T. (2005). Profile likelihood inferences on semiparametric varying-coefficient partially linear models. Bernoulli, 11(6), 1031–1057.CrossRefGoogle Scholar
Friedrich, M., Smeekes, S., & Urbain, J.-P. (2020). Autoregressive wild bootstrap inference for nonparametric trends. Journal of Econometrics, 214(1), 81–109.CrossRefGoogle Scholar
Gao, J., Kanaya, S., Li, D., & Tjøstheim, D. (2015). Uniform consistency for nonparametric estimation in null recurrent time series. Econometric Theory, 31(4), 911–952.CrossRefGoogle Scholar
Giraitis, L., Kapetanios, G., & Yates, T. (2014). Inference on stochastic time-varying coefficient models. Journal of Econometrics, 179(1), 46–65.CrossRefGoogle Scholar
Hamilton, J. D. (1994). Time series analysis, vol. 2. Princeton University Press.CrossRefGoogle Scholar
Hansen, B. E. (1991). Strong laws for dependent heterogeneous processes. Econometric Theory, 7(2), 213–221.CrossRefGoogle Scholar
Hansen, B. E. (2001). The new econometrics of structural change: dating breaks in U.S. labour productivity. Journal of Economic Perspectives, 15(4), 117–128.CrossRefGoogle Scholar
Hansen, B. E. (2008). Uniform convergence rates for kernel estimation with dependent data. Econometric Theory, 24(3), 726–748.CrossRefGoogle Scholar
Kiefer, N. M., & Vogelsang, T. J. (2002). Heteroskedasticity-autocorrelation robust standard errors using the bartlett kernel without truncation. Econometrica, 70(5), 2093–2095.CrossRefGoogle Scholar
Lenza, M., & Primiceri, G. E. (2022). How to estimate a vector autoregression after March 2020. Journal of Applied Econometrics, 37(4), 688–699.CrossRefGoogle Scholar
Li, D., Phillips, P. C. B., & Gao, J. (2016). Uniform consistency of nonstationary kernel-weighted sample covariances for nonparametric regression. Econometric Theory, 32(3), 655–685.CrossRefGoogle Scholar
Li, Q., & Racine, J. (2007). Nonparametric econometrics theory and practice. Princeton University Press.Google Scholar
Lütkepohl, H. (2005). New introduction to multiple time series analysis. Springer Science & Business Media.CrossRefGoogle Scholar
Newey, W. K., & West, K. D. (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica, 55(3), 703–708.CrossRefGoogle Scholar
Petrova, K. (2019). A quasi-Bayesian local likelihood approach to time varying parameter VAR models. Journal of Econometrics, 212(1), 286–306.CrossRefGoogle Scholar
Phillips, P. C. B., & Lee, J. H. (2013). Predictive regression under various degrees of persistence and robust long-horizon regression. Journal of Econometrics, 177(2), 250–264.CrossRefGoogle Scholar
Phillips, P. C. B., Li, D., & Gao, J. (2017). Estimating smooth structural change in cointergration models. Journal of Econometrics, 196(1), 180–195.CrossRefGoogle Scholar
Phillips, P. C. B., & Solo, V. (1992). Asymptotics for linear processes. Annals of Statistics, 20(2), 971–1001.CrossRefGoogle Scholar
Primiceri, G. E. (2005). Time varying structural vector autoregressions and monetary policy. Review of Economic Studies, 72(3), 821–852.CrossRefGoogle Scholar
Primiceri, G. E. (2006). Why inflation rose and fell: Policy-makers’ beliefs and U.S. postwar stabilization policy. Quarterly Journal of Economics, 121(3), 867–901.CrossRefGoogle Scholar
Richter, S., & Dahlhaus, R. (2019). Cross validation for locally stationary processes. Annals of Statistics, 47(4), 2145–2173.CrossRefGoogle Scholar
Shao, X. (2010). The dependent wild bootstrap. Journal of the American Statistical Association, 105(489), 218–235.CrossRefGoogle Scholar
Sims, C., & Zha, T. (2006). Were there regime switches in U.S. monetary policy? American Economic Review, 96(1), 54–81.CrossRefGoogle Scholar
Staiger, D. O., Stock, J. H., & Watson, M. W. (1997). How precise are estimates of the natural rate of unemployment? In C. D. Romer & D. H. Romer (eds.), Reducing inflation: Motivation and strategy (pp. 195–246). University of Chicago Press.Google Scholar
Stock, J. H., & Watson, M. W. (2016a). Core inflation and trend inflation. Review of Economics and Statistics, 98(4), 770–784.CrossRefGoogle Scholar
Stock, J. H., & Watson, M. W. (2016b). Dynamic factor models, factor-augmented vector autoregressions, and structural vector autoregressions in macroeconomics. In J. B. Taylor & H. Uhlig (eds.), Handbook of macroeconomics, vol. 2 (415–525). Elsevier.Google Scholar
Sun, Y., Hong, Y., Lee, T.-H., Wang, S., & Zhang, X. (2021). Time-varying model averaging. Journal of Econometrics, 222(2), 974–992.CrossRefGoogle Scholar
Sun, Y., Phillips, P. C., & Jin, S. (2008). Optimal bandwidth selection in heteroskedasticity–autocorrelation robust testing. Econometrica, 76(1), 175–194.CrossRefGoogle Scholar
Withers, C. (1981). Conditions for linear processes to be strong-mixing. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 57(4), 477–480.CrossRefGoogle Scholar
Xu, K.-L., & Phillips, P. C. (2008). Adaptive estimation of autoregressive models with time-varying variances. Journal of Econometrics, 142(1), 265–280.CrossRefGoogle Scholar
Zhang, T., & Wu, W. B. (2012). Inference of time-varying regression models. Annals of Statistics, 40(3), 1376–1402.CrossRefGoogle Scholar
Zhou, Z., & Wu, W. B. (2010). Simultaneous inference of linear models with time varying coefficients. Journal of the Royal Statistical Society: Series B, 72(4), 513–531.CrossRefGoogle Scholar
Supplementary material: File

Yan et al. supplementary material

Yan et al. supplementary material
Download Yan et al. supplementary material(File)
File 397.2 KB