THE DICKEY–FULLER TEST FOR EXPONENTIAL RANDOM WALKS

Abstract

A common test in econometrics is the Dickey–Fuller test, which is based on the test statistic 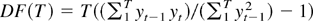. We investigate the behavior of the test statistic if the data y_t are given by an exponential random walk exp(Z_t) where Z_t = Z_t−1 + σε_t and the ε_t are independent and identically distributed random variables. The test statistic DF(T) is a nonlinear transformation of the partial sums of ε_t process. Under certain moment conditions on the ε_t we show that 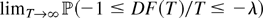tends to one as λ → 0. For the particular case that the ε_t define a simple random walk it is shown that plim_T→∞DF(T)/T exists and the limit is evaluated. The theoretical results are illustrated by some simulation experiments.We gratefully acknowledge the help of an anonymous referee whose comments on the first two versions of this paper enabled us to reduce the number of mistakes and to increase the clarity of presentation. The authors' research was supported in part by Sonderforschungsbereich 475, University of Dortmund.