Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T02:13:34.679Z Has data issue: false hasContentIssue false
  • English
  • Français

HIGHER-ORDER APPROXIMATION OF IV ESTIMATORS WITH INVALID INSTRUMENTS

Published online by Cambridge University Press:  10 November 2022

Byunghoon Kang Open the ORCID record for Byunghoon Kang [Opens in a new window]
Byunghoon Kang*
Affiliation:
Lancaster University
*
Address correspondence to Byunghoon Kang, Department of Economics, Lancaster University, Lancaster, UK; e-mail: b.kang1@lancaster.ac.uk.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper analyzes the higher-order approximation of instrumental variable (IV) estimators in a linear homoskedastic IV regression model when a large set of instruments with potential invalidity is present. We establish theoretical results on the higher-order mean-squared error (MSE) approximation of the two-stage least-squares (2SLS), the limited information maximum likelihood (LIML), the Fuller (FULL), the bias-adjusted 2SLS, and jackknife version of the LIML and FULL estimators by allowing for local violations of the instrument exogeneity conditions. Based on the approximation to the higher-order MSE, we consider the instrument selection criteria that can be used to choose among the set of available instruments. We demonstrate the asymptotic optimality of the instrument selection procedure proposed by Donald and Newey (2001, Econometrica 69, 1161–1191) in the presence of locally (faster than 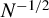$N^{-1/2}$) invalid instruments in the sense that the dominant term in the MSE with the chosen instrument is asymptotically equivalent to the infeasible optimum. Furthermore, we propose instrument selection procedures to choose instruments among the sets of conservative (known) valid instruments and potentially locally (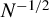$N^{-1/2}$) invalid instruments based on the higher-order MSE of the IV estimators by considering the bias-variance trade-off.

Type
ARTICLES
Information
Econometric Theory , Volume 40 , Issue 4 , August 2024 , pp. 752 - 789
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Footnotes

We thank the Editor (Peter Phillips), the Co-Editor (Patrik Guggenberger), and three anonymous referees for thoughtful comments that significantly improved the paper. The author is grateful to Bruce Hansen for his thoughtful discussions. The author also acknowledges helpful conversations with Jack Porter, Xiaoxia Shi, Francis DiTraglia, Joachim Freyberger, Seojeong Lee, Adam McCloskey, and seminar participants at UW–Madison, MEG 2013, and NEM 2019. This paper is a revised version of the second chapter in the author’s Ph.D. thesis at UW–Madison, and the previous version was also circulated under the title “Choosing a Set of Instruments among Many and Possibly Invalid Instruments.”

References

REFERENCES

Anatolyev, S. & Yaskov, P. (2017) Asymptotics of diagonal elements of projection matrices under many instruments/regressors. Econometric Theory 33, 717–738.CrossRefGoogle Scholar
Anderson, T.W. & Sawa, T. (1973) Distributions of estimates of coefficients of a single equation in a simultaneous system and their asymptotic expansions. Econometrica 41, 683–714.CrossRefGoogle Scholar
Andrews, D.W.K. (1999) Consistent moment selection procedures for generalized method of moments estimation. Econometrica 67, 543–563.CrossRefGoogle Scholar
Andrews, D.W.K. & Lu, B. (2001) Consistent model and moment selection procedures for GMM estimation with application to dynamic panel data models. Journal of Econometrics 101, 123–164.CrossRefGoogle Scholar
Andrews, I. (2019) On the structure of IV Estimands. Journal of Econometrics 211, 294–307.CrossRefGoogle Scholar
Andrews, I., Gentzkow, M., & Shapiro, J.M. (2017) Measuring the sensitivity of parameter estimates to estimation moments. Quarterly Journal of Economics 132, 1553–1592.CrossRefGoogle Scholar
Angrist, J.D., Imbens, G.W., & Krueger, A.B. (1999) Jackknife instrumental variables estimation. Journal of Applied Econometrics 14, 57–67.3.0.CO;2-G>CrossRefGoogle Scholar
Armstrong, T. & Kolesár, M. (2021) Sensitivity analysis using approximate moment condition models. Quantitative Economics 12, 77–108.CrossRefGoogle Scholar
Bekker, P.A. (1994) Alternative approximations to the distributions of instrumental variable estimators. Econometrica 62, 657–681.CrossRefGoogle Scholar
Bekker, P.A. & van der Ploeg, J. (2005) Instrumental variable estimation based on grouped data. Statistica Neerlandica 59, 239–267.CrossRefGoogle Scholar
Belloni, A., Chen, D., Chernozhukov, V., & Hansen, C. (2012) Sparse models and methods for optimal instruments with an application to eminent domain. Econometrica 80, 2369–2430.Google Scholar
Berkowitz, D., Caner, M., & Fang, Y. (2008) Are nearly exogenous instruments reliable? Economics Letters 101, 20–23.CrossRefGoogle Scholar
Berkowitz, D., Caner, M., & Fang, Y. (2012) The validity of instruments revisited. Journal of Econometrics 166, 255–266.CrossRefGoogle Scholar
Bonhomme, S. & Weidner, M. (2022) Minimizing sensitivity to model misspecification. Quantitative Economics 13, 907–954.CrossRefGoogle Scholar
Canay, I. (2010) Simultaneous selection and weighting of moments in GMM using a trapezoidal kernel. Journal of Econometrics 156, 284–303.CrossRefGoogle Scholar
Caner, M. (2014) Near Exogeneity and weak identification in generalized empirical likelihood estimators: Many moment Asymptotics. Journal of Econometrics 182, 247–268.CrossRefGoogle Scholar
Caner, M., Han, X., & Lee, Y. (2018) Adaptive elastic net GMM estimation with many invalid moment conditions: Simultaneous model and moment selection. Journal of Business and Economic Statistics 36, 24–46.CrossRefGoogle Scholar
Carrasco, M. (2012) A regularization approach to the many instruments problem. Journal of Econometrics 170, 383–398.CrossRefGoogle Scholar
Chao, J.C., Hausman, J., Newey, W.K., Swanson, N.R., & Woutersen, T. (2014) Testing overidentifying restrictions with many instruments and heteroskedasticity. Journal of Econometrics 178, 15–21.CrossRefGoogle Scholar
Chao, J.C. & Swanson, N.R. (2005) Consistent estimation with a large number of weak instruments. Econometrica 73, 1673–1692.CrossRefGoogle Scholar
Chao, J.C., Swanson, N.R., Hausman, J., Newey, W.K., & Woutersen, T. (2012) Asymptotic distribution of JIVE in a heteroskedastic IV regression with many instruments. Econometric Theory 28, 42–86.CrossRefGoogle Scholar
Cheng, X. & Liao, Z. (2015) Select the valid and relevant moments: An information-based LASSO for GMM with many moments. Journal of Econometrics 186, 443–464.CrossRefGoogle Scholar
Cheng, X., Liao, Z., & Shi, R. (2019) On uniform asymptotic risk of averaging GMM estimator. Quantitative Economics 10, 931–979.CrossRefGoogle Scholar
Chetty, R., Friedman, J.N., Hilger, N., Saez, E., Schanzenbach, D.W., & Yagan, D. (2011) How does your kindergarten classroom affect your earnings? Evidence from project star. Quarterly Journal of Economics 126, 1593–1660.CrossRefGoogle ScholarPubMed
Conley, T.G., Hansen, C.B., & Rossi, P.E. (2012) Plausibly exogenous. Review of Economics and Statistics 94, 260–272.CrossRefGoogle Scholar
DiTraglia, F. (2016) Using invalid instruments on purpose: Focused moment selection and averaging for GMM. Journal of Econometrics 195, 187–208.CrossRefGoogle Scholar
Donald, S.G., Imbens, G.W., & Newey, W.K. (2009) Choosing instrumental variables in conditional moment restriction models. Journal of Econometrics 152, 28–36.CrossRefGoogle Scholar
Donald, S.G. & Newey, W.K. (1999) Choosing the Number of Instruments. Working paper 99-05, Department of Economics, Massachusetts Institute of Technology. https://dspace.mit.edu/bitstream/handle/1721.1/63410/choosingnumberof00dona.pdf?sequence=1.Google Scholar
Donald, S.G. & Newey, W.K. (2001) Choosing the number of instruments. Econometrica 69, 1161–1191.CrossRefGoogle Scholar
Evdokimov, K. & Kolesár, M. (2019) Inference in Instrumental Variable Regression Analysis with Heterogeneous Treatment Effects. Working paper.Google Scholar
Fuller, W.A. (1977) Some properties of a modification of the limited information estimator. Econometrica 45, 939–953.CrossRefGoogle Scholar
Guggenberger, P. (2008) Finite sample evidence suggesting a heavy tail problem of the generalized empirical likelihood estimator. Econometric Reviews 27, 526–541.CrossRefGoogle Scholar
Guggenberger, P. (2012) On the asymptotic size distortion of tests when instruments locally violate the exogeneity assumption. Econometric Theory 28, 387–421.CrossRefGoogle Scholar
Guggenberger, P. & Kumar, G. (2012) On the size distortion of tests after an overidentifying restrictions pretest. Journal of Applied Econometrics 27, 1138–1160.CrossRefGoogle Scholar
Hahn, J. & Hausman, J. (2005) Estimation with valid and invalid instruments. Annales d’Économie et de Statistique 79/80, 25–57.CrossRefGoogle Scholar
Hahn, J., Hausman, J., & Kuersteiner, G. (2004) Estimation with weak instruments: Accuracy of higher-order bias and MSE approximations. The Econometrics Journal 7, 272–306.CrossRefGoogle Scholar
Hall, A.R. & Inoue, A. (2003) The large sample behavior of the generalized method of moments estimator in misspecified models. Journal of Econometrics 114(2), 361–394.CrossRefGoogle Scholar
Hall, A.R. & Peixe, F.P.M. (2003) A consistent method for the selection of relevant instruments. Econometric Reviews 22, 269–287.CrossRefGoogle Scholar
Hansen, C., Hausman, J., & Newey, W.K. (2008) Estimation with many instrumental variables. Journal of Business and Economic Statistics 26, 398–422.CrossRefGoogle Scholar
Hausman, J., Lewis, R., Menzel, K., & Newey, W.K. (2011) Properties of the CUE estimator and a modification with moments. Journal of Econometrics 165, 45–57.CrossRefGoogle Scholar
Hausman, J., Newey, W.K., Woutersen, T., Chao, J.C., & Swanson, N.R. (2012) Instrumental variable estimation with heteroskedasticity and many instruments. Quantitative Economics 3, 211–255.CrossRefGoogle Scholar
Hong, H., Preston, B., & Shum, M. (2003) Generalized empirical likelihood-based model selection criteria for moment condition models. Econometric Theory 19, 923–943.CrossRefGoogle Scholar
Imbens, G.W. & Angrist, J.D. (1994) Identification and estimation of local average treatment effects. Econometrica 62, 467–475.CrossRefGoogle Scholar
Kang, H., Zhang, A., Cai, T.T., & Small, D.S. (2016) Instrumental variables estimation with some invalid instruments and its application to Mendelian randomization. Journal of the American Statistical Association 111, 132–144.CrossRefGoogle Scholar
Kinal, T. (1980) The existence of moments of $k$ -class estimators. Econometrica 48, 241–249.CrossRefGoogle Scholar
Kitamura, Y., Otsu, T., & Evdokimov, K. (2013) Robustness, infinitesimal neighborhoods, and moment restrictions. Econometrica 81, 1185–1201.Google Scholar
Kolesár, M (2013) Estimation in an Instrumental Variables Model with Treatment Effect Heterogeneity. Working paper. https://www.princeton.edu/~mkolesar/papers/late_estimation.pdf.Google Scholar
Kolesár, M., Chetty, R., Friedman, J., Glaeser, E., & Imbens, G.W. (2015) Identification and inference with many invalid instruments. Journal of Business and Economic Statistics 33, 474–484.CrossRefGoogle Scholar
Kraay, A. (2012) Instrumental variables regressions with uncertain exclusion restrictions: A Bayesian approach. Journal of Applied Econometrics 27, 108–128.CrossRefGoogle Scholar
Kuersteiner, G. (2012) Kernel weighted GMM estimators for linear time series models. Journal of Econometrics 170, 399–421.CrossRefGoogle Scholar
Kuersteiner, G. & Okui, R. (2010) Constructing optimal instruments by first-stage prediction averaging. Econometrica 78, 697–718.Google Scholar
Lee, Y. & Okui, R. (2012) Hahn–Hausman test as a specification test. Journal of Econometrics 167, 133–139.CrossRefGoogle Scholar
Lee, Y. & Zhou, Y. (2015) Averaged Instrumental Variables Estimators. Working paper. https://ylee41.expressions.syr.edu/wp-content/uploads/W_AvgIV_LeeZhou.pdf.Google Scholar
Leeb, H. & Pötscher, B.M. (2005) Model selection and inference: Facts and fiction. Econometric Theory 21, 21–59.CrossRefGoogle Scholar
Leeb, H. & Pötscher, B.M. (2008) Sparse estimators and the oracle property, or the return of Hodges’ estimator. Journal of Econometrics 142, 201–211.CrossRefGoogle Scholar
Li, K.C. (1987) Asymptotic optimality for ${C}_p$ , ${C}_L$ , cross-validation and generalized cross-validation: Discrete index set. Annals of Statistics 15, 958–975.CrossRefGoogle Scholar
Liao, Z. (2013) Adaptive GMM shrinkage estimation with consistent moment selection. Econometric Theory 29, 857–904.CrossRefGoogle Scholar
Maasoumi, E. & Phillips, P.C.B. (1982) On the behavior of inconsistent instrumental variable estimators. Journal of Econometrics 19, 183–201.CrossRefGoogle Scholar
Mallows, C.L. (1973) Some comments on ${C}_p$ . Technometrics 15, 661–675.Google Scholar
Mariano, R.S. & Sawa, T. (1972) The exact finite-sample distribution of the limited-information maximum likelihood estimator in the case of two included endogenous variables. Journal of the American Statistical Association 67, 159–163.CrossRefGoogle Scholar
Morimune, K. (1983) Approximate distributions of $k$ -class estimators when the degree of overidentifiability is large compared with the sample size. Econometrica 51, 821–841.CrossRefGoogle Scholar
Nagar, A.L. (1959) The bias and moment matrix of the general $k$ -class estimators of the parameters in simultaneous equations. Econometrica 27, 575–595.CrossRefGoogle Scholar
Nevo, A. & Rosen, A. (2012) Identification with imperfect instruments. Review of Economics and Statistics 94, 659–671.CrossRefGoogle Scholar
Newey, W.K. (1985) Generalized method of moments specification testing. Journal of Econometrics 29, 229–256.CrossRefGoogle Scholar
Newey, W.K. (1997) Convergence rates and asymptotic normality for series estimators. Journal of Econometrics 79, 147–168.CrossRefGoogle Scholar
Newey, W.K. & Smith, R.J. (2004) Higher order properties of GMM and generalized empirical likelihood estimators. Econometrica 72, 219–255.CrossRefGoogle Scholar
Newey, W.K. & Windmeijer, F. (2009) Generalized method of moments with many weak moment conditions. Econometrica 77, 687–719.Google Scholar
Okui, R. (2011) Instrumental variable estimation in the presence of many moment conditions. Journal of Econometrics 165, 70–86.CrossRefGoogle Scholar
Otsu, T. (2011) Moderate deviations of generalized method of moments and empirical likelihood estimators. Journal of Multivariate Analysis 102, 1203–1216.CrossRefGoogle Scholar
Pfanzagl, J. & Wefelmeyer, W. (1978) A third-order optimum property of the maximum likelihood estimator. Journal of Multivariate Analysis 8, 1–29.CrossRefGoogle Scholar
Phillips, G. & Hale, C. (1977) The bias of instrumental variable estimators of simultaneous equation systems. International Economic Review 18, 219–228.CrossRefGoogle Scholar
Phillips, P.C.B. (1980) The exact distribution of instrumental variable estimators in an equation containing $n+1$ endogenous variables. Econometrica 48(4), 861–878.CrossRefGoogle Scholar
Phillips, P.C.B. (1983) Exact small sample theory in the simultaneous equations model. In Griliches, Z. & Intriligator, M.D. (eds.), Handbook of Econometrics , vol. 1, pp. 449–516. North-Holland.CrossRefGoogle Scholar
Phillips, P.C.B. (2003) Vision and influence in econometrics: John Denis Sargan. Econometric Theory 19, 495–511.Google Scholar
Rothenberg, T.J. (1984) Approximating the distributions of econometric estimators and test statistics. In Griliches, Z. & Intriligator, M.D. (eds.), Handbook of Econometrics , vol. 2, pp. 881–935. Elsevier.CrossRefGoogle Scholar
Sargan, J.D. (1982) On Monte Carlo estimates of moments that are infinite. In Basmann, R.I. & Rhodes, G.F. (eds.), Advances in Econometrics: A Research Annual , pp. 267–299. JAI Press.Google Scholar
Schennach, S.M. (2007) Point estimation with exponentially tilted empirical likelihood. Annals of Statistics 35, 634–672.CrossRefGoogle Scholar
Staiger, D. & Stock, J.H. (1997) Instrumental variables regression with weak instruments. Econometrica 65, 557–586.CrossRefGoogle Scholar
van Hasselt, M. (2010) Many instruments asymptotic approximations under nonnormal error distributions. Econometric Theory 26, 633–645.CrossRefGoogle Scholar
Windmeijer, F., Farbmacher, H., Davies, N., & Smith, G.D. (2018) On the use of the Lasso for instrumental variables estimation with some invalid instruments. Journal of the American Statistical Association 114, 1339–1350.CrossRefGoogle ScholarPubMed
Supplementary material: PDF

Kang supplementary material

Kang supplementary material

Download Kang supplementary material(PDF)
PDF 546.7 KB