Article contents
LEAST SQUARES AND IVX LIMIT THEORY IN SYSTEMS OF PREDICTIVE REGRESSIONS WITH GARCH INNOVATIONS
Published online by Cambridge University Press: 23 March 2021
Abstract
The paper examines the effect of conditional heteroskedasticity on least squares inference in stochastic regression models of unknown integration order and proposes an inference procedure that is robust to models within the (near) I(0)–(near) I(1) range with GARCH innovations. We show that a regressor signal of exact order 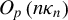 $O_{p}\left ( n\kappa _{n}\right ) $ for arbitrary
$O_{p}\left ( n\kappa _{n}\right ) $ for arbitrary  $\,\kappa _{n}\rightarrow \infty $ is sufficient to eliminate stationary GARCH effects from the limit distributions of least squares based estimators and self-normalized test statistics. The above order dominates the
$\,\kappa _{n}\rightarrow \infty $ is sufficient to eliminate stationary GARCH effects from the limit distributions of least squares based estimators and self-normalized test statistics. The above order dominates the 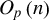 $O_{p}\left ( n\right ) $ signal of stationary regressors but may be dominated by the
$O_{p}\left ( n\right ) $ signal of stationary regressors but may be dominated by the 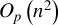 $O_{p}\left ( n^{2}\right ) $ signal of I(1) regressors, thereby showing that least squares invariance to GARCH effects is not an exclusively I(1) phenomenon but extends to processes with persistence degree arbitrarily close to stationarity. The theory validates standard inference for self normalized test statistics based on the ordinary least squares estimator when
$O_{p}\left ( n^{2}\right ) $ signal of I(1) regressors, thereby showing that least squares invariance to GARCH effects is not an exclusively I(1) phenomenon but extends to processes with persistence degree arbitrarily close to stationarity. The theory validates standard inference for self normalized test statistics based on the ordinary least squares estimator when  $\kappa _{n}\rightarrow \infty $ and
$\kappa _{n}\rightarrow \infty $ and 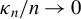 $\kappa _{n}/n\rightarrow 0$ and the IVX estimator (Phillips and Magdalinos (2009a), Econometric Inference in the Vicinity of Unity. Working paper, Singapore Management University; Kostakis, Magdalinos, and Stamatogiannis, 2015a, Review of Financial Studies 28(5), 1506–1553.) when
$\kappa _{n}/n\rightarrow 0$ and the IVX estimator (Phillips and Magdalinos (2009a), Econometric Inference in the Vicinity of Unity. Working paper, Singapore Management University; Kostakis, Magdalinos, and Stamatogiannis, 2015a, Review of Financial Studies 28(5), 1506–1553.) when  $\kappa _{n}\rightarrow \infty $ and the innovation sequence of the system is a covariance stationary vec-GARCH process. An adjusted version of the IVX–Wald test is shown to also accommodate GARCH effects in purely stationary regressors, thereby extending the procedure’s validity over the entire (near) I(0)–(near) I(1) range of regressors under conditional heteroskedasticity in the innovations. It is hoped that the wide range of applicability of this adjusted IVX–Wald test, established in Theorem 4.4, presents an advantage for the procedure’s suitability as a tool for applied research.
$\kappa _{n}\rightarrow \infty $ and the innovation sequence of the system is a covariance stationary vec-GARCH process. An adjusted version of the IVX–Wald test is shown to also accommodate GARCH effects in purely stationary regressors, thereby extending the procedure’s validity over the entire (near) I(0)–(near) I(1) range of regressors under conditional heteroskedasticity in the innovations. It is hoped that the wide range of applicability of this adjusted IVX–Wald test, established in Theorem 4.4, presents an advantage for the procedure’s suitability as a tool for applied research.
Information
- Type
- ARTICLES
- Information
- Econometric Theory , Volume 38 , Issue 5: YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS: PART I , October 2022 , pp. 875 - 912
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
This paper is dedicated to Peter Phillips with gratitude for his mentorship, friendship and generosity over the years.
I would like to thank Don Andrews, Stelios Arvanitis, Ioannis Kasparis, Katerina Petrova, and two anonymous referees for valuable suggestions and comments. Financial support by the British Academy is gratefully acknowledged.
References
REFERENCES
- 3
- Cited by

