Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:50:18.451Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON GENERALIZED EMPIRICAL LIKELIHOOD ESTIMATION OF SEMIPARAMETRIC CONDITIONAL MOMENT RESTRICTION MODELS

Published online by Cambridge University Press:  19 September 2016

Naoya Sueishi
Naoya Sueishi*
Affiliation:
Kobe University
*
*Address correspondence to Naoya Sueishi, Graduate School of Economics, Kobe University, Rokkodai-cho, Nada-ku, Kobe 657-8501, Japan; e-mail: sueishi@econ.kobe-u.ac.jp.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes an empirical likelihood-based estimation method for semiparametric conditional moment restriction models, which contain finite dimensional unknown parameters and unknown functions. We extend the results of Donald, Imbens, and Newey (2003, Journal of Econometrics 117, 55–93) by allowing unknown functions to be included in the conditional moment restrictions. We approximate unknown functions by a sieve method and estimate the finite dimensional parameters and unknown functions jointly. We establish consistency and derive the convergence rate of the estimator. We also show that the estimator of the finite dimensional parameters is 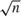$\sqrt n$-consistent, asymptotically normally distributed, and asymptotically efficient.

Type
MISCELLANEA
Information
Econometric Theory , Volume 33 , Issue 5 , October 2017 , pp. 1242 - 1258
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Early versions of this paper were titled “Generalized Empirical Likelihood Estimation via Conditional Moment Restrictions Containing Unknown Functions.” This paper is based on part of my dissertation at the University of Wisconsin. I would like to thank Bruce Hansen and Jack Porter for their helpful comments and suggestions. The comments from a co-editor and two referees improved the paper. I also thank Yoshihiko Nishiyama, Kohtaro Hitomi, Qingfeng Liu, Ryo Okui, and seminar participants at Kobe University, Kyoto University, and University of Wisconsin. All remaining errors are mine.

References

REFERENCES

Ai, C. & Chen, X. (2003) Efficient estimation of models with conditional moment restrictions containing unknown functions. Econometrica 71, 1795–1843.CrossRefGoogle Scholar
Blundell, R., Chen, X., & Kristensen, D. (2007) Semi-nonparametric IV estimation of shape-invariant Engel curves. Econometrica 75, 1613–1669.CrossRefGoogle Scholar
Carrasco, M. & Florens, J.-P. (2000) Generalization of GMM to a continuum of moment conditions. Econometric Theory 16, 797–834.CrossRefGoogle Scholar
Chamberlain, G. (1987) Asymptotic efficiency in estimation with conditional moment restrictions. Journal of Econometrics 34, 305–334.CrossRefGoogle Scholar
Chen, X. & Pouzo, D. (2009) Efficient estimation of semiparametric conditional moment models with possibly nonsmooth residuals. Journal of Econometrics 152, 46–60.CrossRefGoogle Scholar
Dominguez, M.A. & Lobato, I.N. (2004) Consistent estimation of models defined by conditional moment restrictions. Econometrica 2004, 1601–1615.CrossRefGoogle Scholar
Donald, S.G., Imbens, G.W., & Newey, W.K. (2003) Empirical likelihood estimation and consistent tests with conditional moment restrictions. Journal of Econometrics 117, 55–93.CrossRefGoogle Scholar
Kitamura, Y., Tripathi, G., & Ahn, H. (2004) Empirical likelihood-based inference in conditional moment restriction models. Econometrica 72, 1667–1714.CrossRefGoogle Scholar
Newey, W.K. (1990) Efficient instrumental variable estimation of nonlinear models. Econometrica 58, 809–837.CrossRefGoogle Scholar
Newey, W.K. (1991) Uniform convergence in probability and stochastic equicontinuity. Econometrica 59, 1161–1167.CrossRefGoogle Scholar
Newey, W.K. & Powell, J.L. (2003) Instrumental variable estimation of nonparametric models. Econometrica 71, 1565–1578.CrossRefGoogle Scholar
Newey, W.K. & Smith, R.J. (2004) Higher order properties of GMM and generalized empirical likelihood estimators. Econometrica 72, 219–255.CrossRefGoogle Scholar
Nishiyama, Y., Liu, Q., & Sueishi, N. (2005) Semiparametric estimators for conditional moment restrictions containing nonparametric functions: Comparison of GMM and empirical likelihood procedures. In Zerger, A. & Argent, R.M. (eds.), Proceedings of International Congress on Modelling and Simulation, pp. 926–932. Modelling and Simulation Society of Australia and New Zealand.Google Scholar
Otsu, T. (2011) Empirical likelihood estimation of conditional moment restriction models with unknown functions. Econometric Theory 27, 8–46.CrossRefGoogle Scholar
Qin, J. & Lawless, J. (1994) Empirical likelihood and general estimating equations. Annals of Statistics 22, 300–325.CrossRefGoogle Scholar
Robinson, P.M. (1987) Asymptotically efficient estimation in the presence of heteroskedasticity of unknown form. Econometrica 55, 875–891.CrossRefGoogle Scholar
Shen, X. & Wong, W.H. (1994) Convergence rate of sieve estimates. Annals of Statistics 22, 580–615.CrossRefGoogle Scholar
Smith, R.J. (2006) Efficient information theoretic inference for conditional moment restrictions. Journal of Econometrics 138, 430–460.CrossRefGoogle Scholar
Zhang, J. & Gijbels, I. (2003) Sieve empirical likelihood and extensions of the generalized least squares. Scandinavian Journal of Statistics 30, 1–24.CrossRefGoogle Scholar
Supplementary material: File

Sueishi supplementary material S1

Sueishi supplementary material

Download Sueishi supplementary material S1(File)
File 69.3 KB
Supplementary material: PDF

Sueishi supplementary material S2

Sueishi supplementary material

Download Sueishi supplementary material S2(PDF)
PDF 163 KB