Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heijmans, Risto D.H.
and
Magnus, Jan R.
1986.
Consistent maximum-likelihood estimation with dependent observations.
Journal of Econometrics,
Vol. 32,
Issue. 2,
p.
253.
Kalbfleisch, J. D.
and
Lawless, J. F.
1988.
Estimation of Reliability in Field – Performance Studies.
Technometrics,
Vol. 30,
Issue. 4,
p.
365.
Ruskeepää, Heikki
1991.
A note on estimating equations for linear parameters in discrete-time stochastic processes.
Statistics,
Vol. 22,
Issue. 3,
p.
403.
1994.
Hilbert Space Methods in Probability and Statistical Inference.
p.
235.
Huggins, Richard M.
and
Staudte, Robert G.
1994.
Cell lineage analysis: Variance Components Models for Dependent Cell Populations.
Journal of the American Statistical Association,
Vol. 89,
Issue. 425,
p.
19.
Huggins, R.M.
1994.
Outlier detection tests based on martingale estimating equations for stochastic processes.
Stochastic Processes and their Applications,
Vol. 53,
Issue. 2,
p.
393.
Huggins, Richard
1996.
On the identifiability of measurement error in the bifurcating autoregressive model.
Statistics & Probability Letters,
Vol. 27,
Issue. 1,
p.
17.
Huggins, R. M.
1996.
Robust inference for variance components models for single trees of cell lineage data.
The Annals of Statistics,
Vol. 24,
Issue. 3,
Li, Bing
1996.
A minimax approach to consistency and efficiency for estimating equations.
The Annals of Statistics,
Vol. 24,
Issue. 3,
Wefelmeyer, Wolfgang
1996.
Quasi-likelihood models and optimal inference.
The Annals of Statistics,
Vol. 24,
Issue. 1,
O′Hara Hines, R. J.
1997.
An Application of retrospective sampling in the analysis of a very large clustered data set.
Journal of Statistical Computation and Simulation,
Vol. 59,
Issue. 1,
p.
63.
Markatou, Marianthi
Basu, Ayanendranath
and
Lindsay, Bruce G.
1998.
Weighted Likelihood Equations with Bootstrap Root Search.
Journal of the American Statistical Association,
Vol. 93,
Issue. 442,
p.
740.
Heagerty, Patrick J.
and
Zeger, Scott L.
1998.
Lorelogram: A Regression Approach to Exploring Dependence in Longitudinal Categorical Responses.
Journal of the American Statistical Association,
Vol. 93,
Issue. 441,
p.
150.
Heagerty, Patrick J.
and
Lele, Subhash R.
1998.
A Composite Likelihood Approach to Binary Spatial Data.
Journal of the American Statistical Association,
Vol. 93,
Issue. 443,
p.
1099.
Lele, Subhash
Taper, Mark L.
and
Gage, Stuart
1998.
STATISTICAL ANALYSIS OF POPULATION DYNAMICS INSPACE AND TIME USING ESTIMATING FUNCTIONS.
Ecology,
Vol. 79,
Issue. 5,
p.
1489.
Small, Christopher G.
and
Yang, Zejiang
1999.
Multiple roots of estimating functions.
Canadian Journal of Statistics,
Vol. 27,
Issue. 3,
p.
585.
Lee, Y.
and
Nelder, John A.
1999.
The robustness of the quasilikelihood estimator.
Canadian Journal of Statistics,
Vol. 27,
Issue. 2,
p.
321.
Bui, Q.M
and
Huggins, R.M
1999.
Inference for the random coefficients bifurcating autoregressive model for cell lineage studies.
Journal of Statistical Planning and Inference,
Vol. 81,
Issue. 2,
p.
253.
Li, David X.
and
Turtle, H. J.
2000.
Semiparametric ARCH Models: An Estimating Function Approach.
Journal of Business & Economic Statistics,
Vol. 18,
Issue. 2,
p.
174.
Li, Bing
2000.
Nonparametric estimating equations based on a penalized information criterion.
Canadian Journal of Statistics,
Vol. 28,
Issue. 3,
p.
621.

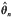 resulting from estimating equations g
resulting from estimating equations g