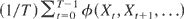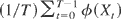Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bec, Frédérique
Rahbek, Anders
and
Shephard, Neil
2008.
The ACR Model: A Multivariate Dynamic Mixture Autoregression*.
Oxford Bulletin of Economics and Statistics,
Vol. 70,
Issue. 5,
p.
583.
Fokianos, Konstantinos
Rahbek, Anders
and
Tjostheim, Dag
2008.
Poisson Autoregression.
SSRN Electronic Journal,
Fokianos, Konstantinos
Rahbek, Anders
and
Tjøstheim, Dag
2009.
Poisson Autoregression.
Journal of the American Statistical Association,
Vol. 104,
Issue. 488,
p.
1430.
Cavaliere, Giuseppe
Rahbek, Anders
and
Taylor, A. M. Robert
2009.
Co-Integration Rank Testing under Conditional Heteroskedasticity.
SSRN Electronic Journal,
Kristensen, Dennis
and
Rahbek, Anders
2010.
Likelihood-based inference for cointegration with nonlinear error-correction.
Journal of Econometrics,
Vol. 158,
Issue. 1,
p.
78.
Cavaliere, Giuseppe
Rahbek, Anders
and
Taylor, A.M. Robert
2010.
COINTEGRATION RANK TESTING UNDER CONDITIONAL HETEROSKEDASTICITY.
Econometric Theory,
Vol. 26,
Issue. 6,
p.
1719.
Peter Boswijk, H.
and
van der Weide, Roy
2011.
Method of moments estimation of GO-GARCH models.
Journal of Econometrics,
Vol. 163,
Issue. 1,
p.
118.
Lange, Theis
Rahbek, Anders
and
Jensen, Søren Tolver
2011.
Estimation and Asymptotic Inference in the AR-ARCH Model.
Econometric Reviews,
Vol. 30,
Issue. 2,
p.
129.
Fokianos, Konstantinos
and
Tjøstheim, Dag
2012.
Nonlinear Poisson autoregression.
Annals of the Institute of Statistical Mathematics,
Vol. 64,
Issue. 6,
p.
1205.
Kirch, Claudia
and
Kamgaing, Joseph Tadjuidje
2012.
Testing for parameter stability in nonlinear autoregressive models.
Journal of Time Series Analysis,
Vol. 33,
Issue. 3,
p.
365.
Rahbek, Anders
and
Nielsen, Heino Bohn
2012.
Unit Root Vector Autoregression with Volatility Induced Stationarity.
SSRN Electronic Journal,
Ekner, Line Elvstrrm
and
Nejstgaard, Emil
2013.
Parameter Identification in the Logistic STAR Model.
SSRN Electronic Journal,
Kristensen, Dennis
and
Rahbek, Anders
2013.
TESTING AND INFERENCE IN NONLINEAR COINTEGRATING VECTOR ERROR CORRECTION MODELS.
Econometric Theory,
Vol. 29,
Issue. 6,
p.
1238.
Nielsen, Heino Bohn
and
Rahbek, Anders
2014.
Unit root vector autoregression with volatility induced stationarity.
Journal of Empirical Finance,
Vol. 29,
Issue. ,
p.
144.
Elsaied, Hanan
and
Fried, Roland
2014.
ROBUST FITTING OF INARCH MODELS.
Journal of Time Series Analysis,
Vol. 35,
Issue. 6,
p.
517.
Xiong, Lanyu
and
Zhu, Fukang
2019.
Robust quasi-likelihood estimation for the negative binomial integer-valued GARCH(1,1) model with an application to transaction counts.
Journal of Statistical Planning and Inference,
Vol. 203,
Issue. ,
p.
178.
Dahl, Christian M.
and
Iglesias, Emma M.
2021.
Asymptotic normality of the MLE in the level-effect ARCH model.
Statistical Papers,
Vol. 62,
Issue. 1,
p.
117.
Elsaied, Hanan
and
Fried, Roland
2021.
On robust estimation of negative binomial INARCH models.
METRON,
Vol. 79,
Issue. 2,
p.
137.
Sathish, Vurukonda
Mukhopadhyay, Siuli
and
Tiwari, Rashmi
2022.
Autoregressive and moving average models for zero‐inflated count time series.
Statistica Neerlandica,
Vol. 76,
Issue. 2,
p.
190.
Toure, Cheikh
Auger, Anne
and
Hansen, Nikolaus
2023.
Global linear convergence of evolution strategies with recombination on scaling-invariant functions.
Journal of Global Optimization,
Vol. 86,
Issue. 1,
p.
163.