Article contents
PREDICTIVE DENSITY ESTIMATION FOR MULTIPLE REGRESSION
Published online by Cambridge University Press: 15 January 2008
Abstract
Suppose we observe X ∼ Nm(Aβ,σ2I) and would like to estimate the predictive density p(y|β) of a future Y ∼ Nn(Bβ,σ2I). Evaluating predictive estimates 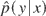 by Kullback–Leibler loss, we develop and evaluate Bayes procedures for this problem. We obtain general sufficient conditions for minimaxity and dominance of the “noninformative” uniform prior Bayes procedure. We extend these results to situations where only a subset of the predictors in A is thought to be potentially irrelevant. We then consider the more realistic situation where there is model uncertainty and this subset is unknown. For this situation we develop multiple shrinkage predictive estimators and obtain general minimaxity and dominance conditions. Finally, we provide an explicit example of a minimax multiple shrinkage predictive estimator based on scaled harmonic priors.We acknowledge Larry Brown, Feng Liang, Linda Zhao, and three referees for their helpful suggestions. This work was supported by various NSF grants, DMS-0605102 the most recent.
by Kullback–Leibler loss, we develop and evaluate Bayes procedures for this problem. We obtain general sufficient conditions for minimaxity and dominance of the “noninformative” uniform prior Bayes procedure. We extend these results to situations where only a subset of the predictors in A is thought to be potentially irrelevant. We then consider the more realistic situation where there is model uncertainty and this subset is unknown. For this situation we develop multiple shrinkage predictive estimators and obtain general minimaxity and dominance conditions. Finally, we provide an explicit example of a minimax multiple shrinkage predictive estimator based on scaled harmonic priors.We acknowledge Larry Brown, Feng Liang, Linda Zhao, and three referees for their helpful suggestions. This work was supported by various NSF grants, DMS-0605102 the most recent.
Information
- Type
- Research Article
- Information
- Copyright
- © 2008 Cambridge University Press
References
REFERENCES
- 10
- Cited by

