Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-13T02:29:13.720Z Has data issue: false hasContentIssue false
  • English
  • Français

STRUCTURAL CHANGE IN NONSTATIONARY AR(1) MODELS

Published online by Cambridge University Press:  24 July 2017

Tianxiao Pang ,
Terence Tai-Leung Chong ,
Danna Zhang  and
Yanling Liang
Tianxiao Pang*
Affiliation:
Zhejiang University
Terence Tai-Leung Chong
Affiliation:
The Chinese University of Hong Kong Nanjing University
Danna Zhang
Affiliation:
University of California
Yanling Liang
Affiliation:
Zhejiang University
*
*Address correspondence to Tianxiao Pang, School of Mathematical Sciences, Yuquan Campus, Zhejiang University, Hangzhou 310027, P.R. China; e-mail: txpang@zju.edu.cn.
Get access Rights & Permissions [Opens in a new window]

Abstract

This article revisits the asymptotic inference for nonstationary AR(1) models of Phillips and Magdalinos (2007a) by incorporating a structural change in the AR parameter at an unknown time k0. Consider the model ${y_t} = {\beta _1}{y_{t - 1}}I\{ t \le {k_0}\} + {\beta _2}{y_{t - 1}}I\{ t > {k_0}\} + {\varepsilon _t},t = 1,2, \ldots ,T$, where I{·} denotes the indicator function, one of 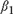${\beta _1}$ and 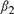${\beta _2}$ depends on the sample size T, and the other is equal to one. We examine four cases: Case (I): 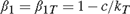${\beta _1} = {\beta _{1T}} = 1 - c/{k_T}$, 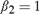${\beta _2} = 1$; (II): 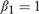${\beta _1} = 1$, 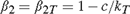${\beta _2} = {\beta _{2T}} = 1 - c/{k_T}$; (III): 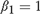${\beta _1} = 1$, 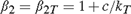${\beta _2} = {\beta _{2T}} = 1 + c/{k_T}$; and case (IV): 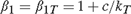${\beta _1} = {\beta _{1T}} = 1 + c/{k_T}$, 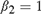${\beta _2} = 1$, where c is a fixed positive constant, and kT is a sequence of positive constants increasing to ∞ such that kT = o(T). We derive the limiting distributions of the t-ratios of 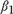${\beta _1}$ and 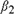${\beta _2}$ and the least squares estimator of the change point for the cases above under some mild conditions. Monte Carlo simulations are conducted to examine the finite-sample properties of the estimators. Our theoretical findings are supported by the Monte Carlo simulations.

Type
ARTICLES
Information
Econometric Theory , Volume 34 , Issue 5 , October 2018 , pp. 985 - 1017
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Tianxiao Pang and Yanling Liang’s research was supported by the Department of Education of Zhejiang Province in China (N20140202).

References

REFERENCES

Anderson, T.W. (1959) On asymptotic distributions of estimates of parameters of stochastic difference equations. The Annals of Mathematical Statistics 30(3), 676–687.CrossRefGoogle Scholar
Bai, J. (1997) Estimating multiple breaks one at a time. Econometric Theory 13(3), 315–352.CrossRefGoogle Scholar
Bai, J. & Perron, P. (1998) Estimating and testing linear models with multiple structural changes. Econometrica 66(1), 47–78.CrossRefGoogle Scholar
Bai, J., Chen, H., Chong, T.T.L., & Wang, S.X. (2008) Generic consistency of the break-point estimators under specification errors in a multiple-break model. The Econometrics Journal 11(2), 287–307.CrossRefGoogle Scholar
Barsky, R.B. (1987) The Fisher hypothesis and the forecastability and persistence of inflation. Journal of Monetary Economics 19(1), 3–24.CrossRefGoogle Scholar
Berkes, I., Horváth, L., Ling, S., & Schauer, J. (2011) Testing for structural change of AR model to threshold AR model. Journal of Time Series Analysis 32(5), 547–565.CrossRefGoogle Scholar
Burdekin, R.C.K. & Siklos, P.L. (1999) Exchange rate regimes and shifts in inflation persistence: Does nothing else matter? Journal of Money, Credit and Banking 31(2), 235–247.CrossRefGoogle Scholar
Chan, N.H. & Wei, C.Z. (1987) Asymptotic inference for nearly nonstationary AR(1) processes. The Annals of Statistics 15(3), 1050–1063.CrossRefGoogle Scholar
Chong, T.T.L. (2001) Structural change in AR(1) models. Econometric Theory 17(1), 87–155.CrossRefGoogle Scholar
Chong, T.T.L. (2003) Generic consistency of the break-point estimator under specification errors. The Econometrics Journal 6(1), 167–192.CrossRefGoogle Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, 2nd ed., vol. 2. John Wiley and Sons.Google Scholar
Halunga, A.G. & Osborn, D.R. (2012) Ratio-based estimators for a change point in persistence. Journal of Econometrics 171(1), 24–31.CrossRefGoogle ScholarPubMed
Hansen, B.E. (2001) The new econometrics of structural change: Dating breaks in U.S. labor productivity. The Journal of Economic Perspectives 15(4), 117–128.CrossRefGoogle Scholar
Hakkio, C.S. & Rush, M. (1991) Is the budget deficit “too large”? Economic Inquiry 29(3), 429–445.CrossRefGoogle Scholar
Harvey, D.I., Leybourne, S.J., & Sollis, R. (2017) Improving the accuracy of asset price bubble start and end date estimators. Journal of Empirical Finance 40, 121–138.CrossRefGoogle Scholar
Harvey, D.I., Leybourne, S.J., & Taylor, A.M.R. (2006) Modified tests for a change in persistence. Journal of Econometrics 134(2), 441–469, and Corrigendum. Journal of Econometrics 168(2), 407.CrossRefGoogle Scholar
Huang, S.H., Pang, T.X., & Weng, C.G. (2014) Limit theory for moderate deviations from a unit root under innovations with a possibly infinite variance. Methodology and Computing in Applied Probability 16(1), 187–206.CrossRefGoogle Scholar
Kejriwal, M., Perron, P., & Zhou, J. (2013) Wald tests for detecting multiple structural changes in persistence. Econometric Theory 29(2), 289–323.CrossRefGoogle Scholar
Kim, J. & Pollard, D. (1990) Cube root asymptotics. The Annals of Statistics 18(1), 191–219.CrossRefGoogle Scholar
Lee, S., Seo, M.H., & Shin, Y. (2016) The lasso for high dimensional regression with a possible change point. Journal of the Royal Statistical Society Statistical Methodology Series B 78(1), 193–210.CrossRefGoogle ScholarPubMed
Leybourne, S., Kim, T., Smith, V., & Newbold, P. (2003) Tests for a change in persistence against the null of difference-stationarity. The Econometrics Journal 6(2), 291–311.CrossRefGoogle Scholar
Magdalinos, T. (2012) Mildly explosive autoregression under weak and strong dependence. Journal of Econometrics 169(2), 179–187.CrossRefGoogle Scholar
Mandelbrot, B. (1963) The variation of certain speculative prices. The Journal of Business 36(4), 394–419.CrossRefGoogle Scholar
Mankiw, N.G. & Miron, J.A. (1986) The changing behavior of the term structure of interest rates. The Quarterly Journal of Economics 101(2), 211–228.CrossRefGoogle Scholar
Mankiw, N.G., Miron, J.A., & Weil, D.N. (1987) The adjustment of expectations to a change in regime: A study of the founding of the Federal Reserve. The American Economic Review 77(3), 358–374.Google Scholar
Pang, T. & Zhang, D. (2015) Asymptotic inferences for an AR(1) model with a change point and possibly infinite variance. Communications in Statistics-Theory and Methods 44(22), 4848–4865.CrossRefGoogle Scholar
Pang, T., Zhang, D., & Chong, T.T.L. (2014) Asymptotic inferences for an AR(1) model with a change point: Stationary and nearly non-stationary cases. Journal of Time Series Analysis 35(2), 133–150.CrossRefGoogle Scholar
Phillips, P.C.B. (1987) Towards a unified asymptotic theory for autoregression. Biometrika 74(3), 535–547.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007a) Limit theory for moderate deviations from a unit root. Journal of Econometrics 136(1), 115–130.CrossRefGoogle Scholar
Phillips, P.C.B. & Magdalinos, T. (2007b) Limit theory for moderate deviations from unity under weak dependence. In Phillips, G.D.A. & Tzavalis, E. (eds.), The Refinement of Econometric Estimation and Test Procedures: Finite Sample and Asymptotic Analysis, pp. 123–162. Cambridge University Press.CrossRefGoogle Scholar
Phillips, P.C.B. & Shi, S.P. (2017) Financial bubble implosion and reverse regression. Econometric Theory, first published online 07 June 2017. https://doi.org/10.1017/S0266466617000202.CrossRefGoogle Scholar
Phillips, P.C.B., Shi, S., & Yu, J. (2015a) Testing for multiple bubbles: Historical episodes of exuberance and collapse in the S&P 500. International Economic Review 56(4), 1043–1078.CrossRefGoogle Scholar
Phillips, P.C.B., Shi, S., & Yu, J. (2015b) Testing for multiple bubbles: Limit theory of real-time detectors. International Economic Review 56(4), 1079–1134.CrossRefGoogle Scholar
Phillips, P.C.B., Shi, S., & Yu, J. (2015c) Online supplementary material to “Supplement to two papers on multiple bubbles”. International Economic Review 56(4).Google Scholar
Phillips, P.C.B., Wu, Y., & Yu, J. (2011) Explosive behavior in the 1990s Nasdaq: When did exuberance escalate asset values? International Economic Review 52(1), 201–226.CrossRefGoogle Scholar
Phillips, P.C.B. & Yu, J. (2011) Dating the timeline of financial bubbles during the subprime crisis. Quantitative Economics 2(3), 455–491.CrossRefGoogle Scholar
Pitarakis, J.-Y. (2004) Least squares estimation and tests of breaks in mean and variance under misspecification. The Econometrics Journal 7(1), 32–54.CrossRefGoogle Scholar
Qu, Z. (2008) Testing for structural change in regression quantiles. Journal of Econometrics 146(1), 170–184.CrossRefGoogle Scholar
Stock, J.H. & Watson, M.W. (1996) Evidence on structural instability in macroeconomic time series relations. Journal of Business & Economic Statistics 14(1), 11–30.Google Scholar
Stock, J.H. & Watson, M.W. (1999) A comparison of linear and nonlinear univariate models for forecasting macroeconomic time series. In Engle, R.F. & White, H. (eds.), Cointegration, Causality and Forcasting: A Festschrift in Honour of Clive. W. J. Granger, pp. 1–44. Oxford University Press.Google Scholar
Supplementary material: PDF

Pang supplementary material

Pang supplementary material 1

Download Pang supplementary material(PDF)
PDF 154.6 KB
Supplementary material: File

Pang supplementary material

Pang supplementary material 2

Download Pang supplementary material(File)
File 74.9 KB