Are long-lived persons utility monsters?

Abstract

Nozick’s ‘utility monster’ is often regarded as impossible, because one life cannot be better than a large number of other lives. Against that view, I propose a purely marginalist account of utility monster defining the monster by a higher sensitivity of well-being to resources (instead of a larger total well-being), and I introduce the concept of collective utility monster to account for resource predation by a group. Since longevity strengthens the sensitivity of well-being to resources, large groups of long-lived persons may, if their longevity advantage is sufficiently strong, fall under the concept of collective utility monster, against moral intuition.

1. Introduction

In his critique of utilitarianism, Nozick (1974: 41) argued:

Utilitarian theory is embarrassed by the possibility of utility monsters who get enormously greater sums of utility from any sacrifice of others than these others lose. For, unacceptably, the theory seems to require that we all be sacrificed in the monster’s maw, in order to increase total utility.

The extent to which the utility monster case can serve as a decisive argument against utilitarianism has been widely debated among philosophers. In Reasons and Persons, Parfit (1984: 389) questioned the coherence of Nozick’s utility monster scenario:

As described by Nozick, such a person is a deep impossibility. The world’s population is now several billion. Let us imagine the wretchedness of all these people if they are denied anything above starvation rations, and all other resources go to Nozick’s imagined Monster. Nozick tells us to suppose that this imagined person would be so happy, or have a life of such high quality, that this is the distribution that produces the greatest sum of happiness, or the greatest amount of whatever makes life worth living. How can this be true, given the billions left in wretchedness that could be so easily relieved by a small fraction of this Monster’s vast resources? For this to be true, this Monster’s quality of life must be millions of times as high as that of anyone we know. Can we imagine this? Think of the life of the luckiest person that you know, and ask what a life would have to be like in order to be a million times as much worth living. … It seems a fair reply that we cannot imagine, even in the dimmest way, the life of this Utility Monster. And this casts doubt on the force of the example.

Parfit argues that Nozick’s utility monster is deeply impossible, and, hence, that Nozick’s utility monster case cannot serve as a convincing criticism against utilitarianism. However, when examining the Repugnant Conclusion, Parfit underlines that the imagined population Z – where billions of persons live a very poor life – can be interpreted as another – more plausible – utility monster. Parfit (1984: 389) underlines that:

This imagined population is another Utility Monster. The difference is that the greater sum of happiness comes from a vast increase, not in the quality of one person’s life, but in the number of lives lived. And my Utility Monster is neither deeply impossible, nor something that we cannot imagine.

Parfit thinks that a possible kind of utility monster could take the form of an extremely large population, favouring, from a utilitarian perspective, the sacrifice of each of its members in terms of quality of lives for the sake of increasing the quantity of lives. ¹

In this article, I will re-examine the conditions of existence of Nozick’s utility monsters. I will focus on the particular point raised by Parfit (1984) concerning the implausibility of utility monsters, and leave other issues aside. ² In order to re-examine whether or not the existence of Nozick’s utility monsters is as deeply impossible as Parfit argued, I will consider particular candidates for utility monsters, who are neither imagined beings with an extraordinary capacity to enjoy their life, nor imagined extremely large populations (as population Z), but (groups of) persons who have a longer life than other persons. This article will examine the formal relationship between inequalities in longevity and the existence of Nozick’s utility monsters in a general class of resource distribution problems.

At this stage, it should be stressed that our study of the relationship between utility monsters and long-lived persons takes longevity inequalities as given, and, as such, differs from the philosophical literature dedicated to choices of an optimal length of life under utilitarianism. That literature studied the selection of a length of life to highlight some unattractive implications of utilitarianism. In particular, Cowen (1989) proposed a paradoxical result – the Methuselah Paradox – which is a variant of Parfit’s Repugnant Conclusion, but based on multiplying life-periods rather than lives: ‘for any possibly ecstatically happy and profound life of, say, 200 years, we can imagine another, much longer life which will welfare-dominate it simply by multiplying many years of epsilon utility’ (Cowen 1989: 37). ³

It should also be stressed here that this paper examines a particular criticism of utilitarianism under unequal longevity – the one inspired by Nozick’s monster case – but will deliberately ignore other criticisms of utilitarianism in that context. Other objections include, for instance, Fleurbaey et al. (2014), who argue that utilitarianism has corollaries contradicting the idea of compensating short-lived persons for well-being losses caused by their early death. ⁴ This paper will not consider that objection, and will focus only on whether or not Nozick’s utility monster case can be used to criticize utilitarianism under unequal longevity. ⁵

The present article will study the relationship between inequalities in longevity – taken as given – and the existence of Nozick’s utility monsters. In other words, our goal is to examine whether or not the utilitarian distribution of resources under unequal longevities can be subject to Nozick’s utility monster critique. At the conceptual level, this paper will first argue, against Parfit, that the primary characteristic of Nozick’s utility monster is a higher sensitivity, at the margin, of well-being to resources, rather than a higher total well-being level. Our analysis will then reveal that, under basic assumptions on the structure of lifetime well-being, a longevity advantage strengthens the sensitivity of well-being to resources, which is the primary characteristic leading to the predation of resources under utilitarianism. A logical implication of that structural feature is that, although a long-lived person (taken separately) cannot, under realistic conditions, be a utility monster, a large group of long-lived persons can, if their longevity advantage is sufficiently high, be a ‘collective utility monster’, i.e. a group that would capture (almost) all resources under utilitarianism. More precisely, under some conditions about what ‘letting too few resources to ordinary persons’ means, large groups of long-lived persons can, under a high longevity advantage, fall under the concept of ‘collective utility monster’, against common moral intuition. It should be stressed, however, that the normative relevancy of that implication of Nozick’s monster critique as an objection against utilitarianism can only be assessed provided one compares the conditions under which long-lived persons fall under the concept of ‘collective utility monster’ with our ideas about what an ‘unacceptable predation of resources’ means.

This paper will proceed in five steps. I will first provide a precise account of Nozick’s utility monster. A key question is whether or not the definition of the ‘utility monster’ involves any requirement regarding levels of well-being, as in Parfit (1984), for whom a monster must have a life that is millions of times better than other lives. In section 2, I will argue that such a requirement does not constitute a necessary component of what a utility monster is. I will argue that the primary characteristic of a utility monster consists of a higher marginal well-being level rather than of a higher total well-being level. Then, in a second stage, section 3 will present a purely marginalist account of ‘utility monster’ by defining the concept of S-utility monster, i.e. a person with a sensitivity of well-being so high that she would capture all resources under utilitarianism except – at most – a fraction S of the egalitarian allocation left to each ordinary person. While this account does some justice to Nozick’s critique, it excludes the possibility of a group of persons capturing (almost) all resources under utilitarianism. To allow for collective predation, section 4 will define an S-collective utility monster as a group of persons who would, under utilitarianism, capture all resources except – at most – a fraction S of the egalitarian allocation left to each ordinary person. In a fourth step, section 5 will consider a cake-division problem between ordinary persons (enjoying a normal lifespan) and long-lived persons. Section 5 will demonstrate that, under general conditions, a longevity advantage strengthens the sensitivity of well-being to resources, which is the decisive characteristic leading to the predation of resources under utilitarianism. Then, section 5 will study the conditions under which a group of long-lived persons constitutes an S-collective utility monster, and will examine the normative relevancy of that result as an objection against utilitarianism. In a last step, Section 6 will contrast our results – obtained under a purely marginalist account of Nozick’s utility monster – with Nozick’s own critique of utilitarianism as developed in Anarchy, State and Utopia.

2. Utility Monsters: The Irrelevancy of Well-being Levels

When examining the possibility of existence of utility monsters, Parfit (1984) imposes a particular requirement on such monsters: it must be the case that their lives exhibit a much higher total well-being than the lives of other persons. Parfit considers that utility monsters achieve extremely high well-being levels, that is, that the ‘Monster’s quality of life must be millions of times as high as that of anyone we know’ (Parfit 1984: 389).

Parfit’s account of the utility monster is not purely marginalist: it does not focus only on the stronger capacity of monsters to transform, at the margin, resources into well-being. According to Parfit, the monster is a being that achieves extremely high levels of well-being. This requirement makes the existence of utility monsters hardly plausible. Indeed, it is difficult to imagine a person whose life would be millions of times better than the lives of other persons. From this difficulty, Parfit concludes that utility monsters cannot exist.

While this conclusion follows logically from Parfit’s premises, one can nonetheless question one of these premises. Parfit’s conclusion about the deep impossibility of utility monsters relies on the assumption stating that the achievement of extremely high well-being levels (in comparison to other persons) is a necessary component of what a utility monster is.

To see why that assumption can be questioned, let us examine the context in which Nozick proposed the utility monster case. The utility monster appears in Chapter 3 of Anarchy, State and Utopia, dedicated to the moral constraints to which the State should be subject. Nozick criticized utilitarians, who consider that the State is right to inflict suffering on a person to avoid larger suffering on another person. ⁶ Nozick rejects that logic of State intervention. The utility monster case aims at revealing some unattractive implications of that logic.

In the utility monster case, the utilitarian State would, by redistributing (almost) all resources towards the monster, inflict suffering on (almost) all persons for the sake of avoiding a larger suffering on one person – the monster –, and, hence, would sacrifice the interests of (almost) all persons for the sake of making the monster better off, an unattractive implication. ⁷ This unattractive result – the concentration of (almost) all resources in the ‘maw’ of the monster – does not require that the monster achieves an extremely high level of total well-being, nor a level of well-being larger than the one of other persons. The only requirement for that result is that the well-being of the monster has a larger reactivity or sensitivity to resources in comparison to other persons. This larger sensitivity may, in some cases, lead the monster to achieve higher total levels of well-being than other persons, but this does not need to be the case. Nozick’s utility monster case questions the logic of a State inflicting suffering on persons to avoid larger suffering on other persons, whatever the levels of well-being of the persons are. This explains why no assumption about well-being levels is required. ⁸

To illustrate this point, let us consider simple cake division problems with two persons A and B (Figure 1). Their utility functions U _A (c _A ) and U _B (c _B ) are represented in, respectively, dark grey and light grey. Figure 1 includes two distinct cake division problems. On both graphs, the utility function of person B is flatter than the one of person A. The only difference is that, on the right graph, the utility function of person A has been scaled down by adding a negative constant, making person A worse off than person B. Each graph on Figure 1 shows the distribution of cake that maximizes the sum of utilities, that is, the distribution that equalizes marginal utilities across persons (what Sen (1980) calls ‘utilitarian equality’). ⁹ In the two examples, the utilitarian allocation is the same: person A receives, under utilitarianism, almost the entire cake, because of a higher marginal utility of the cake. On the contrary, person B receives a much smaller piece of cake, because of a flatter utility function.

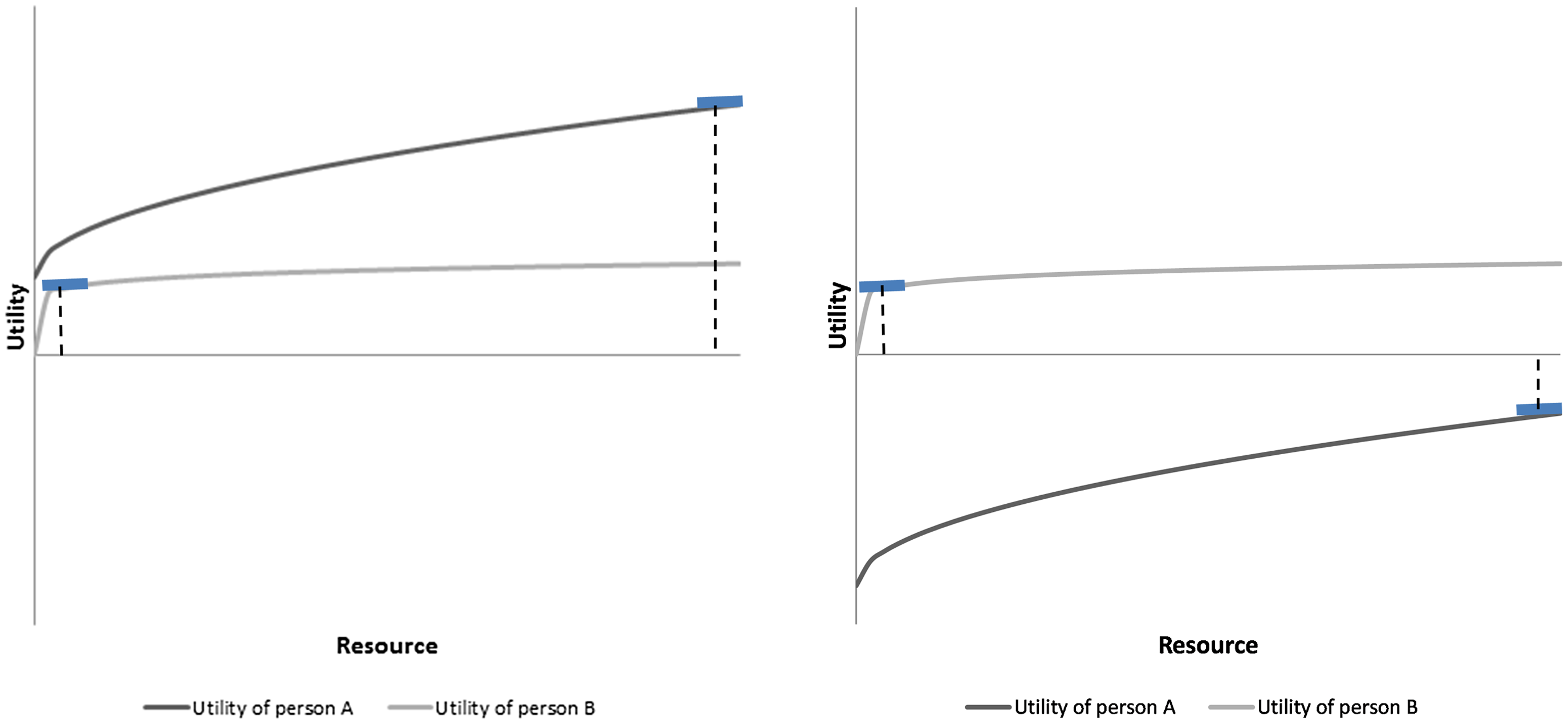
Figure 1. Utilitarian equality in a simple cake division problem.

In each graph, person A is a utility monster, leading to the sacrifice of person B. But it is not the case that person A’s well-being is many times larger than person B’s well-being. Actually, on the right graph, it is even the case that person A, the utility monster, is worse off than person B. This example illustrates that being a utility monster does not require the achievement of a life many times better – or simply better – than other lives. Being a utility monster only requires that one has well-being that is highly sensitive or reactive to resources.

The primary feature of a utility monster is to have a larger sensitivity of well-being to resources. It is that particular feature – and no other – that explains why utilitarianism allocates (almost) all resources to the monster. That characteristic being decisive, there is a strong case for defining a utility monster solely by a larger reactivity of well-being. This view can be called a purely marginalist view of the utility monster. A purely marginalist account of the utility monster focuses only on the sensitivity of the person’s well-being to resources, without any requirement concerning the achieved total well-being level.

Once one accepts this purely marginalist view of utility monster, Parfit’s criticism about the impossibility of a utility monster loses some of its strength. The existence of a utility monster does not require having persons with much higher well-being levels than ordinary persons. True, such persons do not exist and will probably never exist. But this does not tell us anything about the non-existence of utility monsters. Under a purely marginalist view, having a much higher total well-being is not necessary for being a utility monster.

3. A Purely Marginalist Account of a Utility Monster

As shown in section 2, it is a particular characteristic of the utility monster – a larger sensitivity of well-being with respect to other persons – that leads to the concentration of (almost) all resources into the ‘maw’ of the monster. But even if one adopts a purely marginalist account, the definition of a ‘utility monster’ remains incomplete. What does a ‘larger sensitivity of well-being’ mean? This section will present a purely marginalist account of a utility monster allowing for distinct definitions of a ‘larger sensitivity of well-being’.

Consider a resource in total quantity X to be divided among N persons and one person M, the utility monster. Given that the primary characteristic of the monster concerns the sensitivity of well-being to resources, one can hardly define precisely a ‘utility monster’ without specifying individual utility functions. Let us suppose that persons have utility functions U _i (x _i ) where x _i denotes the quantity of the resource enjoyed by person i. Utility functions are supposed to be increasing (i.e. the marginal derivative of U(.) is positive, that is, U _i ’(x _i ) > 0) and concave (i.e. U _i ’’(x _i ) < 0), that is, there is positive but decreasing marginal utility. ¹⁰

Within our framework, the sensitivity of well-being to resources is captured by marginal utilities U _i ’(x _i ). But even when defined in terms of marginal utilities, the ‘higher sensitivity of well-being’ of the monster remains in need of clarification. The sensitivity of well-being varies with the quantity of resources enjoyed by the person, because of the law of decreasing marginal utility. Hence, to characterize a utility monster, one must be explicit under which allocations the marginal utility of the monster exceeds the marginal utilities of other persons.

One approach consists of requiring that a person is a utility monster if and only if her capacity, at the margin, to transform resources into well-being is always larger than the capacity of any other person, whatever the distribution of the resource is. This requirement implies that, to be a monster, a person M must have a marginal utility that exceeds the ones of any other person even when the entire resource is given to M, that is, U _M ’(X) > U _j ’(0) for all j ≠ M. Utilitarianism then gives all resources to M, whereas other persons receive zero.

However, it is not clear that this definition of a ‘higher sensitivity of well-being’ is satisfactory. Is it necessary, to be a utility monster, to let no resource at all to other persons? Or is this characterization of a monster too narrow? It can be argued that a person with a large sensitivity of well-being is a utility monster, even if this sensitivity leads to a utilitarian allocation where other persons receive a small, but strictly positive, amount of the resource. Replacing 0 by a small number does not alter the meaning of being a ‘utility monster’. Thus, a utilitarian allocation where a person M captures almost all resources can be regarded as a situation where M is a utility monster, even if M does not capture the entire resource.

The definition of a utility monster requires thus to clarify what we mean by capturing ‘almost’ all resources. How small do the resources left to persons j ≠ M under utilitarianism have to be to make person M fall under the concept of ‘utility monster’? Given that the term ‘utility monster’ is value-loaded, that question is not a factual one, but an ethical one. One way to formalize that key aspect of a utility monster consists of defining the small amount of resource left to ordinary persons j ≠ M under utilitarianism as a fraction S of the amount X/(1 + N) that would prevail under the egalitarian allocation (in short, a fraction S of the egalitarian allocation). This leads us to the definition of an S-utility monster.

S -utility monster

A person M is an S-utility monster if and only if:

$${U_M}^{\rm{ \unicode{x2019}}}(X - (NSX/(1 + N))) \ge {U_j}{\rm{ \unicode{x2019}}}\left( {SX/\left( {1 + N} \right)} \right)\ for\ all\ j \ne M.$$

where 0 ≤ S < 1 captures how small the share going to each ordinary person j ≠ M under utilitarianism is (as a fraction of the egalitarian allocation).

The definition of the S-utility monster invites several observations. First, this account of the utility monster is a purely marginalist account: this characterizes the utility monster in terms of conditions relative to the sensitivity of well-being to resources, for the monster and other persons. The definition does not include conditions about levels of well-being, but only conditions about the sensitivity of well-being to resources, modelled here as marginal utilities.

In the definition of the S-utility monster, the parameter S captures how small the residue of resources left to ordinary persons j ≠ M under utilitarianism has to be to make person M a ‘utility monster’. When S is 0, the associated ‘0-utility monster’ is a person whose marginal utility of the resource is always higher than the marginal utility of any other person, for all possible allocations of the resource. In that case, utilitarianism concentrates all resources on person M, whereas other persons receive 0. This concept of 0-utility monster is too narrow to capture Nozick’s critique, since the number 0 can be replaced by a small – but strictly positive – number while keeping the intuition that person M is a utility monster. Having stressed this, the issue of how small S has to be in order to do justice to Nozick’s critique remains open.

Taken together, the conditions defining the S-utility monster are necessary and sufficient to have all resources given to the monster under utilitarianism, except – at most – S times the egalitarian allocation X/(1 + N)) left to each ordinary person j ≠ M.

Let us first show the sufficiency of these conditions. Consider the reduction of the share given to the monster from X – (NSX/(1 + N)) to X – (NSX/(1 + N)) – e, and divide e into N equal pieces e/N to be distributed among the N persons. Given U _M ’(X – (NSX/(1 + N))) ≥ U _j ’(SX/(1 + N)), we have, by concavity of utility functions, that U _M ’(X – (NSX/(1 + N)) – e) > U _j ’((SX/(1 + N)) + e/N), implying that transferring the piece e/N from person j to the monster would increase the sum of utilities. Moreover, since U _M ’(X – (NSX/(1 + N)) – e + (e/N)) > U _k ’((SX/(1 + N)) + e/N), redistributing a piece e/N from another person k to the monster would also raise the sum of utilities. The same rationale can be reproduced for all pieces e/N. Hence the conditions defining the S-utility monster imply that, at the utilitarian allocation, the monster captures all resources except – at most – S times the egalitarian allocation given to each ordinary person.

An important corollary of this is the following: to obtain the outcome where (almost) all the resource is given to the monster under utilitarianism, it is not necessary that the marginal utility for the monster when he has all the resource except S times the egalitarian allocation left to each ordinary person j ≠ M, that is, U _M ’(X – (NSX/(1 + N))), is larger than the sum of marginal utilities for the N persons having a fraction S of the egalitarian allocation, that is, ∑U _j ’(SX/(1 + N)). It is sufficient that U _M ’(X – (NSX/(1 + N))) ≥ U _j ’(SX/(1 + N)) for each j. Even if there are millions of ordinary persons, a condition on the marginal utility of the monster with respect to the one of each other person suffices so that the monster obtains all resources except – at most – S times the egalitarian allocation left to each ordinary person.

It can also be shown that the conditions defining the S-utility monster are necessary to have that the utilitarian allocation involves giving all the resource to person M, except – at most – S times the egalitarian allocation left to each ordinary person j ≠ M. To prove this, one can proceed by reductio ad absurdum. Suppose that we have, for a person j ≠ M, the inequality: U _M ’(X – (NSX/(1 + N))) < U _j ’(SX/(1 + N)). Hence, taking a small amount c of the resource from person M, and giving it to person j must increase the total sum of well-being. ¹¹ But if a transfer from person M to person j increases the sum of well-being, it cannot be the case that the initial allocation leaving – at most – S times the egalitarian allocation to each ordinary person is the utilitarian allocation. We have thus reached a contradiction.

4. Collective Utility Monsters

Although it captures key aspects of the idea of ‘utility monster’, our concept of S-utility monster suffers from a major limitation. It defines the utility monster by means of a comparison between one person with a high marginal utility – the monster – and N ordinary persons. This kind of ‘one against all’ comparison does not do entire justice to Nozick’s critique. When developing his critique of utilitarianism, Nozick considered ‘utility monsters’ in the plural, and not necessarily a unique person capturing (almost) all resources.

However, the definition of the S-utility monster excludes the non-uniqueness of the S-utility monster in the population. To see this, consider a person M with a high marginal utility to the resource. Person M is an obvious candidate for falling under the concept of an S-utility monster. Then, duplicate person M into person M’. The mere existence of that replica prevents M from being qualified as an S-utility monster. Indeed, once person M’ exists, it is no longer true that M exhibits a higher sensitivity of well-being than any other person in the population. Thus, once person M’ exists, person M can no longer be qualified as an S-utility monster.

This is an important limitation of our account of the utility monster, because there is no reason to exclude the possibility of predation of resources by a group of persons with a high sensitivity of well-being. In his objection against utilitarianism, Nozick was concerned with the unattractiveness of the predation of (almost) all resources by some persons. From an ethical perspective, the predation of resources by, let us say, two or three persons, is (nearly) as unattractive as the predation by one person. Hence, the utility monster critique of utilitarianism must allow for the predation of resources by groups that are not singletons.

Whether the monster is one person or a group of persons does not matter from the perspective of Nozick’s critique. The intuition is that Nozick’s target – which motivated the utility monster case – is the idea that the State is right to inflict suffering on some persons in order to avoid larger suffering on other persons. ¹² Hence, from the perspective of Nozick’s critique, whether or not the inflicted suffering allows to avoiding larger suffering for one person or for a group of persons does not matter. This motivates us to consider the extension of the concept of S-utility monster to the – related – concept of S-collective utility monster.

Accounting for collective predation requires to give up the ‘one against all’ framework of section 3, and to consider a population partitioned in two groups: on the one hand, a group N including a (strictly positive) number N of ordinary persons; on the other hand, a group O including a (strictly positive) number O of persons with a higher sensitivity of well-being. ¹³ For simplicity, all members of O have the same utility function, denoted by U _m (x _m ). ¹⁴

An important aspect of the definition of a ‘collective utility monster’ concerns whether or not one should specify how small the group O capturing (almost) all resources has to be in comparison with the group N of ordinary persons to fall under the concept of S-collective utility monster. Given that the term ‘monster’ refers, in the natural language, to some kind of anomaly – in opposition to the norm –, it is tempting to require that the size of the collective utility monster must be smaller than the size of the group of ordinary persons. However, incorporating such a constraint would make us depart from Nozick’s intuition behind the construction of the utility monster case. As we showed, Nozick criticized the logic of State intervention that consists in inflicting suffering on persons to avoid a larger suffering for other persons. Nozick’s opposition to that logic does not depend on how large the groups of beneficiaries of the State intervention are. They could be a minority or a majority. This neutrality with respect to how numerous the beneficiaries of State transfers are motivates us to impose no restriction on the sizes of subpopulations N and O in our framework.

Since the group O includes several persons with high marginal utility, each person in O cannot be an S-utility monster. But even if O includes no S-utility monster, it can be the case that this group captures (almost) all resources under utilitarianism, because of the higher marginal utilities of its members. A group that leaves (almost) nothing to the remaining of the population has the ugly appearance of a monster. Hence, when a group captures (almost) all resources under utilitarianism, we call this group a collective utility monster. ¹⁵ As for utility monsters, the definition of ‘collective utility monster’ depends on what one means by ‘capturing (almost) all resources’. This leads us to define the S-collective utility monster.

S -collective utility monster

A group O of O persons with same utility functions is an S-collective utility monster if and only if, for all persons m in O and all persons j in N , we have:

$${U_m}{\rm{\unicode{x2019}}}\left( {\left[ {X-\left( {NSX/\left( {O + N} \right)} \right)} \right]/O} \right) \ge {U_j}{\rm{\unicode{x2019}}}\left( {SX/\left( {O + N} \right)} \right)$$

where 0 ≤ S < 1 captures how small the share going to each ordinary person under utilitarianism is (as a fraction of the egalitarian allocation).

When the group O is a singleton (that is, O = 1), the S-collective utility monster collapses to the S-utility monster of section 3. Indeed, in that case, the conditions concerning the higher sensitivity of well-being coincide exactly with the ones of the S-utility monster. Thus, for a given parameter S describing how small the resources left to each ordinary person have to be in order to be in the presence of an S-collective utility monster, an S-collective utility monster with a unique member is necessarily composed of an S-utility monster as defined previously.

In the general case where the group O includes more than one person, our account of the S-collective utility monster differs from the account of the S-utility monster. A group O can fall under the concept of an S-collective utility monster even if none of its members is, on her own, an S-utility monster. The reason is that, for a given parameter S, the condition, for each person, to be part of an S-collective utility monster is weaker than the condition to be an S-utility monster. The condition to be an S-utility monster concerns the marginal utility of capturing (almost) all resources, whereas the condition to be part of an S-collective utility monster concerns the marginal utility of capturing a fraction 1/O of (almost) all resources. Given the concavity of utility functions, the condition for membership of an S-collective utility monster is weaker than the condition to be an S-utility monster (for a given S).

Finally, it should be stressed that the conditions defining the S-collective utility monster, when taken together, are necessary and sufficient to have that the utilitarian allocation involves giving all resources to group O except – at most – S times the egalitarian allocation given to each ordinary person in group N.

To demonstrate sufficiency, consider the reduction of the share given to the S-collective utility monster from X – (NSX/(O + N)) to X – (NSX/(O + N)) – e, and divide e into N equal pieces e/N distributed among the N ordinary persons. Given U _m ’([X – (NSX/(O + N))]/O) ≥ U _j ’(SX/(O + N)) for each person m in O and each person j in N, we have, by concavity of utility functions, that U _m ’([X – (NSX/(O + N)) – e ]/O) > U _j ’((SX/(O + N)) + e/N), implying that transferring a small amount from an ordinary person j to a person m in O would increase the sum of utilities. The same rationale can be reproduced for each unit e/N. Hence, at the utilitarian optimum, it must be the case, under the condition U _m ’([X – (NSX/(O + N))]/O) ≥ U _j ’(SX/(O + N)) for each person m in O and each person j in N, that the group O captures all resources except – at most – S times the egalitarian allocation given to each ordinary person.

To prove necessity, we can proceed by contradiction. Suppose that the allocation where the group O captures all resources except – at most – S times the egalitarian allocation given to each ordinary person is the utilitarian allocation, and that there is a person m in O and a person j in N such that: U _m ’([X – (NSX/(O + N))]/O) < U _j ’(SX/(O + N)). Under that inequality, transferring a small amount of resources from person m to person j would increase the sum of well-being. But if this is true, the initial allocation where group O captures all resources except – at most – S times the egalitarian allocation given to each ordinary person is not the utilitarian allocation. A contradiction is reached.

5. Utility Monsters and Long-lived Persons

To examine the pure effect of longevity differentials on the distribution of resources under utilitarianism, this section will consider a simple cake division problem among two groups that differ only regarding the length of life of their members, everything else being the same across groups (including temporal utility functions). I will then examine under which conditions long-lived persons can fall under the concept of S-(collective) utility monster.

Consider that a resource in total quantity X is to be allocated within a population that is partitioned in two groups: on the one hand, the group N, which includes N ordinary persons, with a standard length of life whose duration is normalized to unity, and, on the other hand, the group O, which includes O persons, with lives that have a length that is K times the normal length of life, with K > 1. I will call O the group of long-lived persons. ¹⁶

In order to focus on the pure effect of longevity inequality, I assume that members of N and O differ only regarding their longevity. The lifetime well-being of each person j in N is given by a utility function U _j (x _j ), that is the same for all members of the group: U _j (x) = U(x) for all j in N. The lifetime well-being of long-lived persons m in O is the sum, across K periods, of temporal well-being levels measured by the same temporal utility function U(.), and is thus equal to K U(x _m /K). ¹⁷ The utility of being dead is normalized to 0, as usual in the literature.

Throughout this section, I will not make any assumption regarding the levels of well-being for long-lived and short-lived persons because well-being levels are not relevant from the perspective of Nozick’s utility monster case (see section 2). To keep our analysis as general as possible, this section leaves open the question of whether the lifetime well-being of the long-lived is higher/lower than the lifetime well-being of the short-lived. In advanced economies, the total resource X is large, so that it is likely that long-lived persons are better off than short-lived persons. However, in poor economies where resources are extremely scarce, it could be the case that short-lived persons are better off than long-lived persons. ¹⁸

Having stressed this, it is important to underline an important corollary of our framework. Our setting assumes that persons differ only on longevity, but share the same temporal utility function U(.). Hence, it follows that, everything else being left unchanged, long-lived persons have a higher sensitivity of well-being to resources in comparison to short-lived persons. To see this, note that the marginal utility for a short-lived person j in N enjoying a resource x is equal to U’(x). However, the marginal utility for a long-lived person m in O enjoying the same resource x is equal to KU’(x/K)(1/K) = U’(x/K). Given the longevity advantage K > 1, the marginal utility for a long-lived person U’(x/K) is always larger than the marginal utility for a short-lived person U’(x), because of the law of decreasing marginal utility. Thus, a longevity advantage strengthens the sensitivity of well-being to resources, making long-lived persons more sensitive to resources than short-lived persons. ¹⁹

Long-lived persons having a larger sensitivity of well-being to resources, they constitute natural candidates for falling under the concept of Nozick’s utility monster. Are long-lived persons an S-(collective) utility monster? Proposition 1 summarizes our results.

Proposition 1

Consider a population partitioned in groups N and O , whose members have the same temporal utility function, but differ only in their longevity, the members of O having a longevity advantage K over the members of N. The group O is an S-collective utility monster if and only if K is higher than 1/S + ((1/S) – 1)N/O.

Proof: See the Appendix.

Proposition 1 states a necessary and a sufficient condition under which the group of long-lived persons is an S-collective utility monster: the longevity advantage of long-lived persons should be higher than a threshold that is (i) decreasing in the constant S, (ii) increasing in the number of short-lived persons N and (iii) decreasing in the number of long-lived persons O.

The condition stated in Proposition 1, which concerns the size of the longevity advantage of long-lived persons, suffices to make a group of long-lived persons an S-collective utility monster, because a large longevity advantage implies a high sensitivity of well-being to resources – in comparison to ordinary persons –, which makes the group of long-lived persons fall under the concept of S-collective utility monster.

The condition stated in Proposition 1 is not only sufficient, but also necessary to have an S-collective utility monster. The reason is that our framework exhibits a unique dimension of heterogeneity across persons: the length of life. Hence, the only possibility to have an S-collective utility monster – that is, the only possibility to have a higher sensitivity of well-being to resources – consists of having persons with a sufficiently large longevity advantage.

The extent to which the longevity advantage of the long-lived is large enough to make the group of long-lived persons an S-collective utility monster depends on the ethical parameter S, which captures how small the amount of resource left to short-lived persons has to be in order to make long-lived persons be a collective utility monster. If S equals 0, the longevity threshold stated in Proposition 1, equal to plus infinity, is then larger than the longevity advantage K, making the condition for being a 0-collective utility monster unsatisfied. However, for higher levels of S, the threshold for the longevity advantage is lower, and groups of long-lived persons may then fall under the concept of S-collective utility monster.

Let us now examine the other determinants of the threshold for the longevity advantage: the sizes of groups O and N. Consider first the case where the group of long-lived persons is a singleton (O = 1). In that case, Proposition 1 states a necessary and sufficient condition for the unique long-lived person to be an S-utility monster. But when the number of ordinary persons N is sufficiently large, the condition in Proposition 1 is not satisfied. Even a person living as long as purely imaginary beings like Lewis’s Methuselah (Lewis 1976), living 969 years, could not satisfy that condition. Thus a long-lived person, taken on her own, cannot be an S-utility monster. ²⁰ Consider now the general case where the group of long-lived persons is not a singleton (O > 1). Note that the higher the number of long-lived persons O is, the weaker the condition in Proposition 1 is. Therefore, it is possible that, even if no long-lived person taken on her own is an S-utility monster, a sufficiently large group of long-lived persons can, under some circumstances, be an S-collective utility monster.

What does Proposition 1 tell us about real-world societies? To answer that question, it is necessary to distinguish societies existing before and after the demographic transition (the long-run tendency toward a fall of fertility and mortality to low levels). ²¹ Before the demographic transition, long-lived persons were, in relative terms, very few in the society. The number N was much larger than O, making the condition of Proposition 1 not satisfied. But things are different nowadays. Thanks to the improvement of survival conditions, an increasingly large population reaches very old ages. Under these circumstances, the condition of Proposition 1 could be satisfied for some values of the ethical parameter S.

To illustrate this, let us take the example of Australia, where the median age at death is nowadays as large as 84 years for women and 78 years for men (Australian Institute of Health and Welfare 2022). If we take this median age at death as a basis to partition the population in two groups N and O of equal sizes (representing 50% of the total population), this leads approximately to an (average) longevity advantage of between 25 and 30 years for the long-lived, equal to about 40% in relative terms (i.e. K = 1.40). ²² This implies that the condition of Proposition 1 is satisfied for all levels of the parameter S superior to 0.83. Hence, when S exceeds 0.83, long-lived Australian persons form an S-collective utility monster.

Considering the group of long-lived Australian persons as a collective utility monster goes against common moral intuition. However, there is a simple way to reconcile this implication of Proposition 1 with our basic moral judgements. Denying that long-lived Australian persons constitute a collective utility monster can be interpreted as revealing the normative irrelevancy of the concept of ‘S-collective utility monster’ when S is superior to 0.83. In other words, even if the group of long-lived Australian persons consists of an 0.83-collective utility monster, we may regard this fact as normatively irrelevant, on the grounds that letting 83% of the egalitarian allocation to each short-lived person is not, from our moral point of view, an unacceptable predation of resources. If, for instance, one believes that an unacceptable predation requires that less than 10% of the egalitarian allocation is left to each ordinary person, the normatively relevant concept of S-collective utility monster is the concept of 0.1-collective utility monster. Obviously, the group of long-lived Australian persons does not fall under the concept of 0.1-collective utility monster. Long-lived Australian persons are thus not regarded as forming a collective utility monster in a normatively relevant sense.

In the light of this, an important distinction should be made. It is one thing to claim that a group O constitutes an S-collective utility monster. But it is another thing to claim that group O benefits from an unacceptable predation of resources under utilitarianism. From a logical perspective, the second claim does not necessarily follow from the first one. To be able to deduce the second claim from the first one, an additional premise is needed: the normative relevancy of the concept of S-collective utility monster. That additional premise may be considered to be true or false depending on our moral judgements about what an unacceptable predation of resources consists of. These judgements determine which value or interval of values the ethical parameter S should take to make the related concept of S-collective utility monster normatively relevant, and, hence, relevant as an objection against utilitarianism.

6. Back to Nozick’s Critique of Utilitarianism

How can one compare our findings – which are based on a particular formalization of Nozick’s utility monster critique – with Nozick’s own views about utilitarianism?

Following section 5, one may argue that the mere labelling of groups of persons as an S-collective utility monster does not necessarily constitute a convincing argument against utilitarianism. One may defend that it is wrong to be an S-(collective) utility monster only if S is, for instance, below 0.10, but that there is nothing wrong in being an S-(collective) utility monster otherwise (i.e. for higher levels of S). Thus, in the context of longevity inequalities, even if utilitarianism allocates more resources to long-lived persons, the utilitarian allocation does not, under realistic assumptions about the longevity advantage of long-lived persons, make the long-lived fall under the normatively relevant concept of S-collective utility monster (which involves a low value for S). So what’s wrong with utilitarianism?

Whereas that position – which relates the unacceptability of the utilitarian distribution of resources to the value of the ethical parameter S expressing our moral beliefs about what an unacceptable predation consists of – may look attractive for many of us, it should be stressed that this position is not the one adopted by Nozick himself. What is at stake in Nozick’s critique of utilitarianism is the logic that drives redistribution under utilitarianism, rather than its consequences in terms of how small the resources left to ordinary persons are.

Nozick’s critique of utilitarianism questions the logic of distribution based on the sensitivity of well-being to resources. As such, Nozick’s own view is not reducible to a moral belief in a particular value (or interval of values) for the ethical parameter S. From Nozick’s perspective, the problem of utilitarianism is not to imply a too concentrated distribution of resources under some circumstances – as captured, under the concept of S-(collective) utility monster, by the parameter S –, but, rather, to justify redistribution because of ethically irrelevant reasons.

What is at stake in Nozick’s critique is the logic of State redistribution that lies behind utilitarianism. That logic consists of inflicting suffering on some persons to avoid larger suffering on other persons (see section 2). According to Nozick, this logic of redistribution goes against the idea of social justice. The reason is that human beings are separate living entities, who should be treated with dignity and respect. Hence, no human being should be sacrificed for the sake of others’ interests. Nozick’s utility monster case is a situation where some persons are sacrificed for the promotion of other persons’ interests (the persons whose well-being is more sensitive to resources), and, thus, are not treated as separate beings who are owed respect and dignity. ²³

In the context of unequal longevity, the equalization of temporal well-being across all persons is achieved, under utilitarianism, by means of transfers from short-lived persons towards long-lived persons. These transfers are motivated by the logic of inflicting suffering on short-lived persons in order to avoid larger suffering on long-lived persons, whose well-being is more sensitive to resources than the one of the short-lived. From the perspective of Nozick’s critique of utilitarianism, the lower sensitivity of well-being to resources exhibited by short-lived persons does not justify that the State sacrifices the interests of short-lived persons for the sake of promoting the interests of long-lived persons. From Nozick’s perspective, this treatment goes against the idea of social justice, which requires all persons to be treated with dignity and respect, whatever the sensitivity of their well-being is. A short-lived person should be treated with as much respect and dignity as a long-lived person. According to Nozick, utilitarianism fails to do so. Thus Nozick’s condemnation of utilitarianism concerns the logic governing distribution under utilitarianism rather than its distributive implications. As such, Nozick’s critique does not reveal any commitment to a particular value of the ethical parameter S capturing what an unacceptable predation of resources consists of. From Nozick’s perspective, any transfer of resources governed by a logic based on unequal sensitivities of well-being to resources is unacceptable, because it is grounded on ethically irrelevant reasons.

In sum, it is important, at this stage, to distinguish between two separate criticisms of utilitarianism. On the one hand, our formalization, by means of a purely marginalist account, of Nozick’s utility monster as a S-(collective) utility monster, leads to criticize utilitarianism on the ground that it implies a distribution that leaves too few resources to ordinary persons. The scope of that criticism – for the case of longevity inequalities and beyond – depends on the postulated ethical parameter S, which captures how small the residual resources left to each ordinary person have to be to regard the situation as an unacceptable predation. On the other hand, Nozick’s own critique of utilitarianism points to a misleading logic of redistribution under utilitarianism, rather than to its unappealing distributive implications. As such, Nozick’s own criticism does not depend on any value for the ethical parameter S.

7. Conclusions

What do we learn from all this? The main contributions of this article are threefold.

First, contrary to Parfit’s (1984) interpretation of the utility monster case, the primary characteristic of a utility monster lies in a larger sensitivity of well-being to resources, rather than in a higher total well-being level. I thus proposed a purely marginalist account of the utility monster, called the S-utility monster, where the parameter S captures how small resources left to ordinary persons must be in order to be in presence of a monster.

Second, adapting the concept of S-utility monster in such a way as to allow for the collective predation of (almost) all resources by a group of persons having a larger sensitivity of well-being has important implications. A set of persons who, taken one-by-one, would not be counted as S-utility monsters, can nonetheless be, under some conditions, an S-collective utility monster, that is, a group that would capture (almost) all resources under utilitarianism.

Third, when examining the utility monster critique in the context of unequal longevities, it appears that a longevity advantage strengthens the sensitivity of well-being to resources, which is the characteristic leading to the predation of resources under utilitarianism. A logical implication of this structural feature is that, if the longevity advantage is sufficiently high, large groups of long-lived persons may fall under the concept of S-collective utility monster, against common moral intuition. However, as we have seen, it is possible to reconcile this – counterintuitive – result with our basic moral judgements about what an unacceptable predation of resources consists of, by arguing that: (i) our moral judgements reveal that a normatively relevant concept of S-(collective) utility monster involves a low value for the parameter S; (ii) long-lived persons cannot, under realistic conditions about their longevity advantage, fall under a (normatively relevant) concept of S-collective utility monster.

Our formalization of Nozick’s utility monster through the concept of a S-(collective) utility monster could thus, under some moral judgements about what an unacceptable predation of resources is (captured by the parameter S), condemn utilitarianism on the ground of implying, under some circumstances, an unacceptable predation of resources by large groups of long-lived persons, independently from whether long-lived persons are better off or worse off than short-lived persons. As such, this critique differs from the criticism blaming utilitarianism for its insensitivity to the distribution of utilities across persons. Thus it differs from the criticism of utilitarianism on the grounds of transferring resources from the short-lived to the long-lived, despite the latter being better off than the former (Fleurbaey et al. 2014). ²⁴

The formalization of Nozick’s monster critique by means of the concept of S-(collective) utility monster was also shown to differ from Nozick’s own critique of utilitarianism. According to Nozick, what is wrong under utilitarianism is the logic for redistribution based on the sensitivity of well-being to resources, rather than its distributional implications. From Nozick’s point of view, any transfer from short-lived to long-lived persons based on the larger sensitivity of well-being to resources for the latter is wrong, because it is governed by ethically irrelevant reasons (no matter how small resources left to the short-lived are).

The distinction between, on the one hand, Nozick’s critique of utilitarianism and, on the other hand, the critique based on our modelling of Nozick’s utility monster, invites a final remark. By its results, the present study exemplifies the various by-products that can be obtained by trying to formalize ethical arguments such as Nozick’s utility monster case. One by-product is to examine the reducibility of an argument to some fundamental dimensions. In the present case, our formalization of Nozick’s utility monster revealed that utility levels are irrelevant for that argument, and that the utility monster case involves a moral belief about how small resources left to ordinary persons must be to have an unacceptable predation of resources. Another by-product of formalizing an ethical argument consists of a better understanding of the articulation between a particular argument used by a philosopher and the philosopher’s system of thought. Our formalization revealed that Nozick’s utility monster case – which criticizes utilitarianism on the ground of its unappealing distributive implications – is orthogonal to Nozick’s general critique of utilitarianism as a doctrine governed by a misleading logic of distribution (no matter what its distributive implications are).