Deep learning based bias correction of TRMM precipitation estimates using IMD-gridded precipitation as ground observation

Abstract

Bias correction is a critical aspect of data-centric climate studies, as it aims to improve the consistency between observational data and simulations by climate models or estimates by remote sensing. Satellite-based estimates of climatic variables like precipitation often exhibit systematic bias when compared to ground observations. To address this issue, the application of bias correction techniques becomes necessary. This research work examines the use of deep learning to reduce the systematic bias of satellite estimations at each grid location while maintaining the spatial dependency across grid points. More specifically, we try to calibrate daily precipitation values of tropical rainfall measuring mission based TRMM_3B42_Daily precipitation data over Indian landmass with ground observations recorded by India Meteorological Department (IMD). We have focused on the precipitation estimates of the Indian Summer Monsoon Rainfall (ISMR) period (June–September) since India gets more than 75% of its annual rainfall in this period. We have benchmarked these deep learning methods against standard statistical methods like quantile mapping and quantile delta mapping on the above datasets. The comparative analysis shows the effectiveness of the deep learning architecture in bias correction.

Impact Statement

The application of deep learning techniques for bias correction of satellite precipitation data has significantly advanced our ability to obtain more accurate and reliable information for weather monitoring and analysis. This innovative approach addresses inherent biases in satellite precipitation estimates, enhancing the precision of meteorological data and thereby improving the quality of forecasts and climate studies. By mitigating biases in satellite precipitation, this deep learning-based correction method contributes to more informed decision-making processes, ultimately benefiting various sectors reliant on precise and unbiased meteorological information.

1. Introduction

Satellite-based precipitation estimates (SPEs) play a crucial role in providing valuable rainfall data for various applications, including climate research and weather monitoring. However, these rainfall data may be subject to biases due to multiple reasons. Some of the common reasons that introduce bias in SPEs include (i) imperfections in calibration and validation, (ii) sensor limitations, (iii) zonal bias, (iv) topographical effects, and (v) seasonal and regional variability. Hence, researchers and climate scientists often employ bias correction techniques and validation methods to mitigate these issues and improve the reliability of satellite-based rainfall data for various applications, including climate modeling, hydrological studies, and disaster risk assessment. Effective bias correction methods play a pivotal role in addressing systematic biases within climate model outputs and satellite estimations. The primary objective of these correction techniques is to align climate model simulations or SPEs with observational data, to produce reliable precipitation estimates (Tong et al., 2021; Yang et al., 2022).

The literature has shown that many bias correction techniques have been introduced to improve the accuracy of SPEs (Iqbal et al., 2022; Katiraie-Boroujerdy et al., 2020; Sun et al., 2021). The most prevalent statistical methods used in this field can be grouped into two broad categories, i.e., mean-based approaches and distribution-based approaches (Jaiswal et al., 2022; Wei et al., 2022). The mean-based techniques include linear and local intensity-based scaling methods while the distribution-based approaches deal with cumulative distribution functions (Dinh and Aires, 2023; Holthuijzen et al., 2022; Pierce et al., 2015). Quantile mapping and quantile delta mapping are the most popular distribution-based bias correction techniques. These techniques try to establish a functional relationship between the climate model outputs or SPEs and the ground observation (Guo et al., 2019; Irwandi et al., 2023; Passow and Donner, 2020).

The advancement of artificial intelligence techniques and the availability of meteorological data (SPEs and Climate Model Outputs) have introduced a new way to visualize and analyze climate variables. Nowadays, many researchers have expanded their research area to resolve the global and local climate issues (Kumar et al., 2023; Mishra Sharma and Mitra, 2022; Mitra, 2021; Sharma et al., 2023). Again the application of satellite-based products in climate informatics has boosted their research by providing relevant climate data (Chen et al., 2022). The tropical rainfall measuring mission (TRMM)-based precipitation products are one such valuable climate information that helps research studies to understand the characteristics of this hydrometeorological variable.

Along with other climatic research domains, bias correction seems to be the most prominent domain for AI-based researchers. Different research groups of data scientists (Fulton et al., 2023; Kim et al., 2021; Wang and Tian, 2022; Wang et al., 2023) have demonstrated their interest in tackling this climate science challenge. Recent studies on bias correction have highlighted the effectiveness of machine learning and deep learning techniques in rectifying the bias associated with the spatiotemporal climate data (Han et al., 2021; Hu et al., 2021). Researchers like Wang and Tian (2022) have used convolution neural networks to correct the bias present in climate model outputs. Similarly, other groups of researchers (Chen et al., 2022) have used CNN-based models to correct the SPEs.

This research aims to examine the effectiveness and usefulness of deep learning-based architectures for bias correction. Here, the authors have tried to rectify the inherent bias present in the TRMM precipitation estimates by using gauge station-based ground observations. Figure 1 shows the proposed workflow of this work. From Figure 1, it can be identified that the proposed work gives a comparative analysis of different bias correction techniques. Mainly the bias correction ability of both statistical and CNN-based models are examined here.

Figure 1. Flow diagram showing bias correction of SPEs.

The rest of this article is organized as follows: Section 2 introduces the study area and the dataset used for this work. Section 3 discusses the methodologies employed. Section 4 presents the comparative analysis of results for different bias correction techniques using various performance measures. Finally, Section 5 draws the conclusion.

2. Study area and dataset

2.1 Study area

This article concentrates on a designated study area, namely, the mainland of India. The study domain encompasses the latitude range of 6.75°N–38.5°N and the longitude range of 66.5°E–98.25°E. This research specifically incorporates precipitation data solely from the mainland of India, while precipitation values outside the specified area are treated as zero.

2.2 Dataset

In this research, the TRMM_3B42_Daily dataset (Huffman et al., 2016) is employed to illustrate the bias correction techniques. TRMM_3B42_Daily dataset provides gridded rainfall values with spatial resolution 0.25⁰ × 0.25⁰. This dataset is produced by NASA GES DISC from the research-quality 3-hourly TRMM Multi-Satellite Precipitation Analysis (TMPA_3B42). The other dataset used in this work is the IMD daily gridded rainfall dataset with spatial resolution 0.25⁰ × 0.25⁰ (Pai et al., 2014). The IMD precipitation dataset is prepared by the India Meteorological Department from the rain gauge-based ground observations. Since this study focuses on the bias correction of gridded precipitation estimates and India receives more than 75% of its annual rainfall in the ISMR period, we have collected the gridded precipitation data for the ISMR period (June, July, August, and September) only. Here, TRMM dataset is used as the bias data, and the IMD-gridded rainfall dataset serves as the ground observation. Based on the availability of TRMM data samples, we have collected both the biased data and observation samples for the period 1998–2019. The data from 1998–2014 are used for training the deep learning models, and the remaining data are used for testing. The initial samples collected from the IMD-gridded dataset has the shape of 129 × 135. Since we are concentrating on the Indian landmass only, we have excluded some unwanted rows and columns so as to get the required data for the study area mentioned above. The shape of the sample became 128 × 128 after this preprocessing.

The proposed work aims to utilize the temporal relation in the data, so data samples are prepared by considering the temporal axis of the dataset. The three-dimensional convolutional model used in this work has a temporal depth of 10. Hence, each input sample for the model is prepared by taking ten consecutive samples from the TRMM dataset. The proposed work tries to correct the bias present in the Kth sample of TRMM by considering the Kth sample along with nine previous samples of TRMM. The targeted observation for this TRMM sample is the Kth observation of IMD. With this approach, we have prepared 113 input samples per year from the 122 samples available in the ISMR period. The corresponding 113 daily rainfall samples are used for the other bias correction techniques employed in this work. For the quantile-based mapping approaches, the calibration period is considered from 2010 to 2014, while the projection period spans from 2015 to 2019.

3 Methodology

3.1 Statistical methods for bias correction

The widely adopted statistical method for bias correction is the quantile mapping (QM) method. This approach aims to align the distribution of biased data with the distribution of observed data samples. If D_x,y denotes the cumulative distribution function of the dataset x during a time period y, then the bias-corrected satellite data for the projection period are expressed as,

(1) $$ {R}_{BC}={D}_{o,h}^{-1}\left[{D}_{s,p}\left({R}_{s,p}\right)\right] $$

where R represents the variable of interest, and D ⁻¹ denotes the inverse of the cumulative distribution function D. The subscripts p and h signify the projection period and historical period respectively. Additionally, s is employed to represent satellite data, while o is used for observational data.

Another approach in statistical bias correction is the quantile delta mapping (QDM). In QDM, initially, the model projections or biased data undergo detrending based on quantiles, and then the simulated values are bias-corrected using QM with the transfer function established during the calibration period. Subsequently, the relative changes (for precipitation) in quantiles are multiplied with the bias-corrected model outputs to produce the final results.

Mathematically the bias-corrected output for climate variable ‘R’ at time ‘t’ using QDM is given by,

(2) $$ {R}_{BC}=\left[{D}_{o,h}^{-1}\left[{D}_{s,p}^{(t)}\left({R}_{s,p}(t)\right)\right]\right]\times \left[\frac{R_{s,p}(t)}{D_{s,h}^{-1}\left[{D}_{s,p}^{(t)}\left({R}_{s,p}(t)\right)\right]}\right] $$

In the above multiplication, the first term represents the QM-based bias-corrected value at time t and the second term shows the relative change in quantiles.

3.2 Deep learning based bias correction

Super resolution deep residual network

The SRDRN or super resolution deep residual network is a deep learning architecture used for bias correction as well as downscaling of climate data (Wang and Tian, 2022). The SRDRN architecture used in this work has sixteen residual blocks in its encoder part and the encoder receives low-resolution bias data as input. For this model, the low-resolution input samples are prepared from the TRMM data by using bilinear interpolation. The interpolated low-resolution input samples of this model have the shape of 32 × 32. The decoder part of this network has two upsampling blocks, and this part enhances the resolution to get the final bias-corrected high-resolution output sample with dimensions 128 × 128.

Convolutional neural network for bias correction (CNNBC)

Convolutional neural network for bias correction is a 3D-CNN-based model for bias correction. We have proposed this model in our recent work on bias correction of CFS simulations (Mishra Sharma et al., 2024). This model takes a three-dimensional input with depth = 10 and produces the targeted bias-corrected output with depth = 1. The architecture of this model is shown in Figure 2.

Figure 2. Deep learning based CNNBC model.

As shown in Figure 2, this model uses four types of convolutional blocks along with averaging nodes and skip connections. In Figure 2, ‘f’ indicates the number of filters, while ‘k’ and ‘s’ represent the kernel shape and stride, respectively. The first type of convolutional block in CNNBC has a 3D kernel with a shape of (9,9,9) and a stride equal to (1,1,1). The convolutional layer of this block generates 64 feature maps from the single input sample. The second type of block takes the 64 feature maps as input and produces a low-dimensional feature set by using 32 filters. The kernel used in this block has a shape of (3,3,3), and it uses a single stride in all dimensions. The first and second types of convolutional blocks in this model use ReLU as the activation function. These blocks also use dropout layers, which help in regularization and avoid overfitting of the model. The third type of convolutional block used in this network contains a 3D-convolution layer and linear activation. The convolution layer of this block has a single filter and a (5,5,5) kernel. This block has the same stride as that of the first and second blocks. The fourth type of convolutional block of CNNBC has a 3DCNN layer with a kernel shape of (10,1,1) and uses a stride of (10,1,1). This block is used as the final block of the CNNBC model. This block uses a ReLU activation function that provides nonlinearity and truncates the negative estimations. The final layer of CNNBC produces a bias-corrected output sample with a depth of 1. The model is trained by considering MSE as the loss function and ADAM as the optimizer. To regularize the training process, we have used an early stopping criterion with patience set to 20.

4 Result and discussion

In this section, the trained deep learning models and calibrated statistical techniques are evaluated using two state-of-the-art performance measures, namely root-mean-square error (RMSE) and Pearson’s correlation coefficient (R). With these performance measures, a model can be considered most suitable for bias correction if it has a low RMSE value and high correlation.

In this work, the performance measures are calculated at each valid grid point, as well as for the spatial mean rainfall values by comparing the predicted values with the ground observations. In the first step, we calculated these performance measures at each valid grid location. Let, $ {M}_{\left(i,j\right)}^t\hskip0.24em $ represents the model output or predicted value, and $ {O}_{\left(i,j\right)}^t $ represents the observation value for a grid location (i, j) at time t (or test sample t), then the RMSE and correlation (R) value calculated for the grid location (i, j) are mathematically represented as,

(3) $$ {RMSE}_{\left(i,j\right)}=\sqrt{\frac{\sum \limits_{t=1}^T{\left({M}_{\left(i,j\right)}^t-{O}_{\left(i,j\right)}^t\right)}^2}{T}} $$

(4) $$ {R}_{\left(i,j\right)}=\frac{\sum \limits_{t=1}^T\left({O}_{\left(i,j\right)}^t-\hat{O_{\left(i,j\right)}}\right)\left({M}_{\left(i,j\right)}^t-\hat{M_{\left(i,j\right)}}\right)}{\sqrt{\sum \limits_{t=1}^T{\left({O}_{\left(i,j\right)}^t-\hat{O_{\left(i,j\right)}}\right)}^2\sum \limits_{t=1}^T{\left({M}_{\left(i,j\right)}^t-\hat{M_{\left(i,j\right)}}\right)}^2}} $$

Where,

(5) $$ \hat{M_{\left(i,j\right)}}=\frac{\sum \limits_{t=1}^T{M}_{\left(i,j\right)}^t}{T} $$

and,

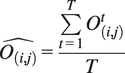(6) $$ \hat{O_{\left(i,j\right)}}=\frac{\sum \limits_{t=1}^T{O}_{\left(i,j\right)}^t}{T} $$

where $ \hat{M_{\left(i,j\right)}} $ and $ \hat{O_{\left(i,j\right)}\;} $ symbolize the mean values of predicted rainfall (bias-corrected rainfall) and observed rainfall, respectively, for the grid location (i, j). Here, T indicates the total number of daily rainfall samples present in the test set.

The grid-wise RMSE values calculated for the biased data as well as for the bias-corrected outputs are depicted in Figure 3. These plots indicate that the deep learning based approaches, especially the CNNBC model, have a lower error rate compared to the other models. The CNNBC model effectively reduces the error present in the biased data for most of the regions across India. Similarly, the gridded correlation values obtained by comparing the model outputs with the observation samples are presented in Figure 4. Here also, we found that the CNNBC model outperforms other statistical and deep learning approaches. Figure 4 clearly shows that the bias-corrected rainfall values obtained by the CNNBC model are highly correlated with the observed precipitation values. The results also indicate that the statistical methods lag behind deep learning-based approaches in maintaining a good correlation between bias-corrected output and observation samples. To further analyze the model performance, we found the average RMSE and correlation values by taking the gridded RMSE and correlation values as presented in Figures 3 and 4, respectively. This average RMSE and correlation value are shown in Table 1. From Table 1, it can be observed that the CNNBC model has a low mean RMSE value and high mean correlation value compared to the other approaches.

Figure 3. Spatial plots showing RMSE values calculated at each grid location.

Figure 4. Spatial plots showing correlation coefficient values calculated at each grid location.

Table 1. Comparison of mean values of gridded RMSE and gridded correlation coefficients

Apart from the grid-wise performance evaluation, we have also carried out the performance evaluation for spatial mean rainfall values. To prepare the mean rainfall samples, we have analyzed the gridded data samples and result samples. We took the area averaged value for each data sample by considering the valid grid locations. If ‘T’ represents the number of result samples and ‘Y’ indicates the number of valid grid locations in each sample, then the spatial mean rainfall value can be represented by a vector X with dimension T, i.e., X = [X₁, X₂,…,X_T]. Here, each X_t indicates the average value of Y grid points at time t.

After preparing the mean rainfall vectors for all the model outputs and observation samples, we calculated the RMSE and correlation coefficient. Let the spatial mean rainfall vector for a model output be represented by $ M $ , and the mean rainfall vector of observation is represented by $ O $ , then the RMSE and correlation coefficient (R) can be calculated by using the following formulas,

(7) $$ RMSE=\sqrt{\frac{\sum \limits_{i=1}^T{\left({M}_i-{O}_i\right)}^2}{T}} $$

(8) $$ R=\frac{\sum \limits_{i=1}^T\left({O}_i-\hat{O}\right)\left({M}_i-\hat{M}\right)}{\sqrt{\sum \limits_{i=1}^T{\left({O}_i-\hat{O}\right)}^2\sum \limits_{i=1}^T{\left({M}_i-\hat{M}\right)}^2}} $$

where T indicates the number of values stored in the vector $ M $ or $ O $ . $ \hat{O} $ and $ \hat{M} $ are used to denote the mean values of observations and predictions, respectively. The results obtained in this examination are shown in Table 2. The results indicate that the use of deep learning models for bias correction reduces the bias present in the daily mean rainfall value by improving the correlation between bias-corrected mean rainfall value and observed mean rainfall value.

Table 2. Performance measures calculated for the daily spatial mean rainfall values

The above analysis indicates that the CNNBC model effectively corrects the bias within the SPEs both at the grid level and for the spatial mean rainfall values. Furthermore, upon comparing the deep learning models used in this study in terms of their learnable parameters and floating-point operations (FLOPs), it is evident that SRDRN contains nearly 39 times more learnable parameters than CNNBC. This suggests that in terms of storage space requirements for the model parameters, CNNBC is much more economical than SRDRN. However, it is also observed that CNNBC requires more FLOPs compared to SRDRN due to its architecture and input–output shape. This highlights a potential avenue for future research, wherein researchers could enhance the CNNBC model to reduce the FLOPs while maintaining performance requirements. Overall, CNNBC appears to be a superior model for bias correction compared to others.

5 Conclusion

The application of deep learning techniques in bias correction of the satellite-based daily precipitation estimates offers promising advancements in enhancing the accuracy and reliability of precipitation estimates. Through the utilization of sophisticated neural network architectures, such as artificial neural networks and convolutional neural networks, significant improvements in bias correction performance can be achieved. By utilizing the vast amounts of data available from satellite estimations, these models can effectively learn complex spatiotemporal patterns inherent in precipitation distributions. To utilize and analyze the power of spatiotemporal convolutional architectures in bias correction, this study performs a comparative analysis between different statistical and deep learning-based bias correction techniques. The main objective of this work is to correct the systematic bias present in the satellite-based TRMM precipitation products. To achieve this goal, four different bias correction techniques, namely, QM, QDM, SRDRN, and CNNCB, are applied to the bias data to get the bias-corrected outputs. The comparative analysis of these models indicates that the CNNBC model is the most suitable model for correcting the daily TRMM precipitation estimates for the specified study area. This research can be further extended by effectively optimizing the proposed architecture to get more reliable and improved bias-corrected results. One more area of future research for this work is the utilization of these models in bias correction of different climatic variables in different geographical locations.