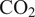Impact statement
Changes in coastal sea level are driven by natural and anthropogenic climate change, with potentially catastrophic consequences for coastal communities. While past studies focused mostly on changes in the mean sea level and extremes, there is less consensus regarding changes in shapes of sea level probability distribution. We fill this void by proposing a new statistical framework to study changes in probability distributions from time series data. The framework can be applied to any climate time series. In the historical period, coastal sea level changes have been driven mainly by a shift in the mean. Changes in shapes of sea level probability distributions could emerge with increasing CO2 concentrations, with possible consequences for sea level extremes attribution studies.
1. Introduction
Regional and global sea levels are affected by both natural climate variations and anthropogenic climate change, with possible repercussions on densely populated coastal communities of great concern. Anthropogenic global warming recently motivated a number of studies characterizing rates and causes of sea level rise since the early 20th century. A reconstruction of global sea level trends since 1900 has been recently proposed by Dangendorf et al. (Reference Dangendorf, Hay and Calafat2019) and Frederikse et al. (Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020). Both studies show a robust increase in mean sea level with trends of
![]() $ 1.6\pm 0.4 $
and
$ 1.6\pm 0.4 $
and
![]() $ 1.56\pm 0.33 $
mm/year over the periods 1900–2015 and 1900–2018, respectively. Such global trends are not constant over time and marked by an acceleration over the recent three decades, as quantified by the
$ 1.56\pm 0.33 $
mm/year over the periods 1900–2015 and 1900–2018, respectively. Such global trends are not constant over time and marked by an acceleration over the recent three decades, as quantified by the
![]() $ 3.1\pm 0.3 $
mm/year trend measured by altimetry since 1993 (WCRP Global Sea Level Budget Group, 2018. This acceleration has been mainly ascribed to an increase in ocean heat uptake driven by changes in Southern Hemisphere westerlies, as well as increased mass loss over Greenland (Dangendorf et al., Reference Dangendorf, Hay and Calafat2019; Frederikse et al., Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020; Fox-Kemper et al., Reference Fox-Kemper, Hewitt, Xiao, Adalgeirsdottir, Drijfhout, Edwards, Golledge, Hemer, Kopp, Krinner, Mix, Notz, Nowicki, Nurhati, Ruiz, Sallee, Slangen, Yu, Masson-Delmotte, Zhai, Pirani, Connors, Pean, Berger, Caud, Chen, Goldfarb, Gomis, Huang, Leitzell, Lonnoy, Matthews, Maycock, Waterfield, Yelekci, Yu and Zhou2021).
$ 3.1\pm 0.3 $
mm/year trend measured by altimetry since 1993 (WCRP Global Sea Level Budget Group, 2018. This acceleration has been mainly ascribed to an increase in ocean heat uptake driven by changes in Southern Hemisphere westerlies, as well as increased mass loss over Greenland (Dangendorf et al., Reference Dangendorf, Hay and Calafat2019; Frederikse et al., Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020; Fox-Kemper et al., Reference Fox-Kemper, Hewitt, Xiao, Adalgeirsdottir, Drijfhout, Edwards, Golledge, Hemer, Kopp, Krinner, Mix, Notz, Nowicki, Nurhati, Ruiz, Sallee, Slangen, Yu, Masson-Delmotte, Zhai, Pirani, Connors, Pean, Berger, Caud, Chen, Goldfarb, Gomis, Huang, Leitzell, Lonnoy, Matthews, Maycock, Waterfield, Yelekci, Yu and Zhou2021).
Globally, the causes of trends in sea level since 1900 are reasonably well understood, with the largest contribution coming from glaciers (52%), followed by ocean thermal expansion (
![]() $ 32\% $
) and Greenland ice sheet mass loss (29%) plus a negative contribution coming from the land water storage (Frederikse et al., Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020). Regionally, on the other hand, sea level can be strongly affected by local variability in patterns of ocean circulation and water masses such as those caused by fluctuations in winds, ocean heating, and moisture fluxes (Han et al., Reference Han, Meehl and Stammer2017; Hamlington et al., Reference Hamlington2020). Such dynamical changes can potentially mask sea level trends in regions dominated by large multidecadal variability. A known example is the observed large trend in sea level in the western Pacific ocean since 1990, mainly reflecting phases of the Pacific decadal oscillation (PDO) (Merrifield et al., Reference Merrifield, Thompson and Lander2012; Zhang and Church, Reference Zhang and Church2012; Han et al., Reference Han, Meehl and Stammer2017). Changes not linked to ocean and atmosphere dynamics also play a role. An example is the vertical land movement in some areas as a consequence of glacial isostatic adjustment (GIA) since the last ice age, causing relatively large differences in long-term trends across basins (Tamisiea, Reference Tamisiea2011; Caron et al., Reference Caron, Ivins, Larour, Adhikari, Nilsson and Blewitt2018; Wang et al., Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021). Notwithstanding the large number of possible contributions, the sea level budget at tide gauges since 1958 has been recently closed in Wang et al. (Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021). The authors identified sterodynamic sea level change as the main contributors to sea level rise in many locations, and GIA in few others (Wang et al., Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021) (as detailed in Gregory et al., Reference Gregory, Griffies and Hughes2019, sterodynamic changes arise from changes in ocean density and ocean circulation).
$ 32\% $
) and Greenland ice sheet mass loss (29%) plus a negative contribution coming from the land water storage (Frederikse et al., Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020). Regionally, on the other hand, sea level can be strongly affected by local variability in patterns of ocean circulation and water masses such as those caused by fluctuations in winds, ocean heating, and moisture fluxes (Han et al., Reference Han, Meehl and Stammer2017; Hamlington et al., Reference Hamlington2020). Such dynamical changes can potentially mask sea level trends in regions dominated by large multidecadal variability. A known example is the observed large trend in sea level in the western Pacific ocean since 1990, mainly reflecting phases of the Pacific decadal oscillation (PDO) (Merrifield et al., Reference Merrifield, Thompson and Lander2012; Zhang and Church, Reference Zhang and Church2012; Han et al., Reference Han, Meehl and Stammer2017). Changes not linked to ocean and atmosphere dynamics also play a role. An example is the vertical land movement in some areas as a consequence of glacial isostatic adjustment (GIA) since the last ice age, causing relatively large differences in long-term trends across basins (Tamisiea, Reference Tamisiea2011; Caron et al., Reference Caron, Ivins, Larour, Adhikari, Nilsson and Blewitt2018; Wang et al., Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021). Notwithstanding the large number of possible contributions, the sea level budget at tide gauges since 1958 has been recently closed in Wang et al. (Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021). The authors identified sterodynamic sea level change as the main contributors to sea level rise in many locations, and GIA in few others (Wang et al., Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021) (as detailed in Gregory et al., Reference Gregory, Griffies and Hughes2019, sterodynamic changes arise from changes in ocean density and ocean circulation).
Trends in sea level at long time scales also impact changes in weather-like extremes. Recently, many studies have focused on quantification of current and future changes in sea level extremes driven by storms, tides, and waves (Buchanan et al., Reference Buchanan, Oppenheimer and Kopp2017; Wahl et al., Reference Wahl, Haigh and Nicholls2017; Rasmussen et al., Reference Rasmussen2018; Sweet et al., Reference Sweet, Genz, Obeysekera and Marra2020; Tebaldi et al., Reference Tebaldi, Ranasinghe and Vousdoukas2021). Such studies aim to characterize tails of sea level distributions in recent periods or in future scenarios via extreme value theory (EVT) (Coles, Reference Coles2001) and often quantify changes in extremes solely as a function of changes in distributional mean (Tebaldi et al., Reference Tebaldi, Ranasinghe and Vousdoukas2021). A shift in the mean sea level is in fact recognized to be the primary driver of changes in tails of the distributions (Vousdoukas et al., Reference Vousdoukas, Mentaschi, Voukouvalas, Verlaan, Jevrejeva, Jackson and Feyen2018; Sreeraj et al., Reference Sreeraj, Swapna, Krishnan, Nidheesh and Sandeep2022. Few studies also explored extreme value analysis by considering changes in the median and width of the fitted generalized extreme value distributions. Examples range from the work of Wong et al. (Reference Wong, Sheets, Torline and Zhang2022), where the authors explored nonstationarity of extreme value statistics covarying with different climate variables, to Lee et al. (Reference Lee, Haran and Keller2017) quantifying links between frequencies of sea level extremes and global mean temperature. Similarly, Grinsted et al. (Reference Grinsted, Moore and Jevrejeva2013) investigated relationships between changes in extreme value analysis in storm surges and different predictors, from the PDO pattern to quasi-biennial oscillation among others.
While recent studies have focused on trends in the mean sea level or on large extremes through EVT, there has been less work quantifying how shapes of sea level probability distributions have been changing in the observational record and how they may change in a warming climate. This is no easy task, as quantifying trends in distributions and their significance under internal climate variability is not a well-defined problem and many measures could be adopted. Le Cozannet et al. (Reference Le Cozannet, Thièblemont, Rohmer, Idier, Manceau and Quique2019) studied changes in sea level distributions in climate models projections focusing on changes in the cumulative distribution functions. Another option would be to directly estimate changes in moments. A useful, comprehensive methodology was recently proposed by McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) where the authors proposed a unified framework to study both linear changes in quantiles and moments of summer temperature time series. Changes in quantiles can be quantified through the quantile regression approach used by Koenker and Bassett (Reference Koenker and Bassett1978) and Koenker and Hallock (Reference Koenker and Hallock2001). Temporal changes in quantiles of the distributions can be further summarized through projections onto few polynomials linking changes in quantiles to changes in statistical moments. McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) empirically showed that Legendre polynomials may be suitable functions for this purpose.
Motivated by quantifying changes in sea level rise and inspired by McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016), here we propose an alternative/complementary route to study temporal changes in probability distributions by building upon McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) in two ways. First, based on the work of Cornish and Fisher (Reference Cornish and Fisher1937), we provide a general, analytical relationship between time changes in quantiles and the first four moments of a distribution. This analytical relationship allows us to build a theoretically founded methodology to explore changes in distributions. We show how the framework allows us to diagnose time changes in distributions as sums of independent shifts in the first four statistical moments. Second, we study the significance of such changes in the presence of internal climate variability by accounting for multiple testings (Benjamini and Hochberg, Reference Benjamini and Hochberg1995). This approach limits the number of false positives in the inference step to obtain trustworthy results even in the presence of a large number of significance tests (James et al., Reference James, Witten, Hastie and Tibshirani2013). Importantly, such linear framework is shown to work well even in case of weak nonlinearities, with few examples shown later with synthetic data in Section 3.4 and in Appendices F and G.
We apply the proposed framework to daily tide gauges data in the 1970–2017 period, for which many locations have reliable data, and in a few locations with longer records. We therefore quantify changes in sea level distributions and assess their significance under the internal variability of the system.
Observational results are then complemented by output from the GFDL-CM4 climate model (Held et al., Reference Held2019. We first focus on the historical experiment and compare it with observations. We then investigate a transient experiment with 1%
![]() $ {\mathrm{CO}}_2 $
increase per year, starting from a preindustrial global
$ {\mathrm{CO}}_2 $
increase per year, starting from a preindustrial global
![]() $ {\mathrm{CO}}_2 $
concentration and extending up to quadrupling after 140 years. Crucially, the modeled trends can be further decomposed into different sea level components. We therefore explore sea level rise as a result of ocean circulation only and when fluctuations in the atmospheric pressure at the sea surface (i.e., sea level pressure [SLP]) are included.
$ {\mathrm{CO}}_2 $
concentration and extending up to quadrupling after 140 years. Crucially, the modeled trends can be further decomposed into different sea level components. We therefore explore sea level rise as a result of ocean circulation only and when fluctuations in the atmospheric pressure at the sea surface (i.e., sea level pressure [SLP]) are included.
The paper is organized as follows. In Section 2, we present the data and the sea level decomposition adopted in this study. Section 3 presents the framework to study shifts in distributions. Results are presented in Section 4, and Section 5 concludes the paper.
2. Datasets
2.1. Observational tide gauge record
We focus on local observations of daily sea level from tide gauge data provided by the University of Hawaii Sea Level Center (Caldwell et al., Reference Caldwell, Merrifield and Thompson2018) (https://uhslc.soest.hawaii.edu/). We first consider the period 1970–2017 and keep only tide gauges with less than 20
![]() $ \% $
missing values. Data gaps are not filled. This step reduces the number of time series considered from 116 to 94. The time range 1970–2017 was chosen as a compromise between retaining high-quality, daily sea level observations and sampling a large portion of coastal areas (e.g., many tide gauges records in Japan do not start before 1969). We then investigate distributional shifts for tide gauges with more than 80 years of data and less than 20
$ \% $
missing values. Data gaps are not filled. This step reduces the number of time series considered from 116 to 94. The time range 1970–2017 was chosen as a compromise between retaining high-quality, daily sea level observations and sampling a large portion of coastal areas (e.g., many tide gauges records in Japan do not start before 1969). We then investigate distributional shifts for tide gauges with more than 80 years of data and less than 20
![]() $ \% $
of missing values, which amounts to 28 available tide gauges. Such long periods translate in a more robust statistical inference of changes in quantiles. For all tide gauges, the daily climatology is removed from each record by subtracting to each day its average over the whole period of interest. Details on the tide gauges preprocessing are further discussed in Appendix A. Start and end recording dates of tide gauges with records longer than 80 years are presented in Appendix B.
$ \% $
of missing values, which amounts to 28 available tide gauges. Such long periods translate in a more robust statistical inference of changes in quantiles. For all tide gauges, the daily climatology is removed from each record by subtracting to each day its average over the whole period of interest. Details on the tide gauges preprocessing are further discussed in Appendix A. Start and end recording dates of tide gauges with records longer than 80 years are presented in Appendix B.
2.2. GFDL-CM4 climate model: Strengths and limitations
We consider outputs from the GFDL-CM4 model (Held et al., Reference Held2019). The ocean component is the MOM6 ocean model (Adcroft et al., Reference Adcroft, Anderson, Balaji, Blanton, Bishuk and Dufour2019) with horizontal grid spacing of 0.25° and 75 vertical layers. With this grid spacing, the model cannot resolve many coastal bays and harbors. Nonetheless, the horizontal grid spacing of 0.25° allows to realistically represent the sloping of continental shelves and its sharp deepening at the boundaries with the open oceans. Such important feature cannot be represented in traditional 1° coupled models. Accurate representation of coastal geometry is key to trustworthy simulations of storm surges and coastal sea level as discussed in Yin et al. (Reference Yin, Griffies, Winton, Zhao and Zanna2020).
The atmospheric/land component is the AM4 model (Zhao, Reference Zhao2018a,Reference Zhaob) with a horizontal grid spacing of roughly 1° and 33 vertical layers. Despite its relatively coarse grid spacing, the model simulates the physical characteristics of tropical cyclones reasonably well, allowing one to study their frequency and changes under different forcings (Zhao, Reference Zhao2018a). However, strong hurricanes (i.e., category 4 and 5) are not simulated, hence their impact on sea level extremes cannot be assessed in our study (Zhao, Reference Zhao2018a; Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020).
A drawback in CM4 is the missing contribution to sea level rise caused by melting of land ice due to the lack of an ice sheet model, similarly to most coupled models in the Coupled Model Intercomparison Project-phase 6 (CMIP6) (Eyring et al., Reference Eyring, Bony, Meehl, Senior, Stevens, Stouffer and Taylor2016). Tides are not simulated and the associated tide surges (Rego and Li, Reference Rego and Li2018), driven by constructive interactions of tides and storm surges, are absent from CM4. Climate-unrelated factors such as GIA and terrestrial water storage, both relevant to sea level (mean) trends (Wang et al., Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021), are also not simulated by this model. As shown by Winton et al. (Reference Winton, Adcroft, Dunne, Held, Shevliakova and Zhao2020), CM4 is a high climate sensitivity model, and so it is likely too sensitive to anthropogenic forcing. A thorough investigation of CM4-model biases in terms of sea level variability was presented in Yin et al. (Reference Yin, Griffies, Winton, Zhao and Zanna2020). Despite some of its limitations, the authors showed that the GFDL-CM4 model can serve as a useful framework to explore changes in sea level statistics under different forcing scenarios. It thus directly serves our interests in the present study.
The focus here is on two simulations. First, we consider one historical experiment in CM4, from 1970 to 2014 with external forcings consistent with observations. Second, we focus on an idealized experiment with a 1%
![]() $ {\mathrm{CO}}_2 $
increase per year (hereafter “1pctCO2”). This experiment simulates the climate system under a 1% increase of
$ {\mathrm{CO}}_2 $
increase per year (hereafter “1pctCO2”). This experiment simulates the climate system under a 1% increase of
![]() $ {\mathrm{CO}}_2 $
per year for 150 years, from preindustrial global
$ {\mathrm{CO}}_2 $
per year for 150 years, from preindustrial global
![]() $ {\mathrm{CO}}_2 $
concentrations up to quadrupling at year 140. We assume that the anthropogenic signal of sea level rise emerges during the first 50 years of the simulation (as shown by Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020 for the US east coast) and focus only on the last 100 years. The 1pctCO2 experiment is especially useful since under an incremental, yearly increase in
$ {\mathrm{CO}}_2 $
concentrations up to quadrupling at year 140. We assume that the anthropogenic signal of sea level rise emerges during the first 50 years of the simulation (as shown by Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020 for the US east coast) and focus only on the last 100 years. The 1pctCO2 experiment is especially useful since under an incremental, yearly increase in
![]() $ {\mathrm{CO}}_2 $
concentration, sea level statistics are expected to change almost linearly (at least in the last 100 years). This linear change allows us to leverage the framework proposed in Section 3 and to explore the emergence of changes in distributional shapes in coastal sea levels.
$ {\mathrm{CO}}_2 $
concentration, sea level statistics are expected to change almost linearly (at least in the last 100 years). This linear change allows us to leverage the framework proposed in Section 3 and to explore the emergence of changes in distributional shapes in coastal sea levels.
The model output is remapped to a uniform 0.5° grid and only grid cells in the latitudinal range
![]() $ \left[-60{}^{\circ},60{}^{\circ}\right] $
are considered. In both simulations, outputs are daily averages. We focus only on coastal locations, accounting for 6,318 time series in each case.
$ \left[-60{}^{\circ},60{}^{\circ}\right] $
are considered. In both simulations, outputs are daily averages. We focus only on coastal locations, accounting for 6,318 time series in each case.
2.3. Sea level decomposition
Following Gill and Niiler (Reference Gill and Niiler1973), Yin et al. (Reference Yin, Griffies and Stouffer2010), and Griffies and Greatbatch (Reference Griffies and Greatbatch2012), we decompose the sea level time tendency in a hydrostatic and Boussinesq ocean according to the following sea level budget
where
![]() $ \Delta $
refers to a temporal increment relative to an initial time. Variables
$ \Delta $
refers to a temporal increment relative to an initial time. Variables
![]() $ \eta, {P}_b,{P}_a $
, and
$ \eta, {P}_b,{P}_a $
, and
![]() $ \rho $
, respectively, represent the sea level, bottom, and surface pressure and density at time
$ \rho $
, respectively, represent the sea level, bottom, and surface pressure and density at time
![]() $ t $
and longitude, latitude, vertical position
$ t $
and longitude, latitude, vertical position
![]() $ \left(x,y,z\right) $
. We make the Boussinesq approximation, which accounts for the constant reference density
$ \left(x,y,z\right) $
. We make the Boussinesq approximation, which accounts for the constant reference density
![]() $ {\rho}_0 $
(e.g., Section 2.4 of Vallis, Reference Vallis2017).
$ {\rho}_0 $
(e.g., Section 2.4 of Vallis, Reference Vallis2017).
In Eq. (1),
![]() $ {P}_b $
is the ocean bottom pressure, so that
$ {P}_b $
is the ocean bottom pressure, so that
![]() $ \Delta {P}_b/\left({\rho}_0\hskip0.1em g\right) $
measures the change in sea level associated with changes in water column mass. Changes in water column mass arise from the convergence of mass via ocean currents as well as water crossing the ocean free surface via precipitation, evaporation, river runoff, and sea ice formation/melt. The SLP,
$ \Delta {P}_b/\left({\rho}_0\hskip0.1em g\right) $
measures the change in sea level associated with changes in water column mass. Changes in water column mass arise from the convergence of mass via ocean currents as well as water crossing the ocean free surface via precipitation, evaporation, river runoff, and sea ice formation/melt. The SLP,
![]() $ {P}_a $
, is caused by atmospheric and sea ice loading. The contribution from
$ {P}_a $
, is caused by atmospheric and sea ice loading. The contribution from
![]() $ {P}_a $
is referred to as the inverse barometer (e.g., Ponte, Reference Ponte2006), whereby increases in
$ {P}_a $
is referred to as the inverse barometer (e.g., Ponte, Reference Ponte2006), whereby increases in
![]() $ {P}_a $
lead to a decrease in sea level. The final term in the budget (1) is the local steric effect, which is measured by the depth integral of changes to in situ ocean density. For example, a decrease in column integrated density, such as through ocean warming or freshening, leads to a sea level rise from local steric expansion.
$ {P}_a $
lead to a decrease in sea level. The final term in the budget (1) is the local steric effect, which is measured by the depth integral of changes to in situ ocean density. For example, a decrease in column integrated density, such as through ocean warming or freshening, leads to a sea level rise from local steric expansion.
Changes from bottom pressure and the local steric effect are associated with ocean dynamics and ocean density and are referred to as sterodynamic sea level changes (Gregory et al., Reference Gregory, Griffies and Hughes2019). Following the CMIP6 convention detailed in Appendix H of Griffies et al. (Reference Griffies, Danabasoglu, Durack, Adcroft, Balaji, Böning, Chassignet, Enrique Curchitser, Drange, Fox-Kemper, Gleckler, Gregory, Haak, Hallberg, Heimbach, Hewitt, Holland, Tatiana Ilyina, Komuro, Krasting, Large, Marsland, Masina, McDougall, Nurser, Orr, Pirani, Qiao, Stouffer, Taylor, Anne Marie Treguier, Uotila, Valdivieso, Wang, Winton and Yeager2016), the sea level diagnostic “zos” measures the regional sterodynamic changes by setting the global mean to zero at each diagnostic time step, with Griffies et al. (Reference Griffies, Danabasoglu, Durack, Adcroft, Balaji, Böning, Chassignet, Enrique Curchitser, Drange, Fox-Kemper, Gleckler, Gregory, Haak, Hallberg, Heimbach, Hewitt, Holland, Tatiana Ilyina, Komuro, Krasting, Large, Marsland, Masina, McDougall, Nurser, Orr, Pirani, Qiao, Stouffer, Taylor, Anne Marie Treguier, Uotila, Valdivieso, Wang, Winton and Yeager2016) referring to zos as the dynamic sea level. There have been many studies of changes to the global mean sea level (e.g., Bittermann et al., Reference Bittermann, Rahmstorf, Kopp and Kemp2017; Le Bars et al., Reference Le Bars, Drijfhout and de Vries2017; Frederikse et al., Reference Frederikse, Landerer, Caron, Adhikari, Parkes, Humphrey, Dangendorf, Hogarth, Zanna and Cheng2020; Palmer et al., Reference Palmer, Domingues, Slangen and Dias2021; among many others), with Yin et al. (Reference Yin, Griffies, Winton, Zhao and Zanna2020) discussing the global thermosteric sea level rise in the CM4 model used here. When comparing models to observations, the global thermosteric sea level must be added to the dynamic sea level at every location in the ocean. However, our interest concerns changes in higher order moments that are independent of changes in the global mean sea level. Therefore, we focus our analysis on the dynamic sea level and inverse barometer only.
We furthermore focus on the anomaly patterns of the inverse barometer (i.e, we remove the daily climatology). Note that the inverse barometer contribution is not explicitly simulated by CMIP5 models. We thus diagnose this term offline by saving the SLP from the atmospheric model. As for tide gauges, we remove the climatological daily cycle from all fields before performing our analysis.
3. Methodology
In this work, we aim to quantify linear changes in sea level distributions in the observational records and climate model output. The methodology is general and can be potentially applied to any climate observable with close-to-linear changes in distributions.
Given a sea level time series, we apply quantile regression to measure linear trends in quantiles (Koenker and Bassett, Reference Koenker and Bassett1978; Portnoy and Koenker, Reference Portnoy and Koenker1997; Koenker and Hallock, Reference Koenker and Hallock2001). We then introduce a set of orthogonal functions and project the quantile slopes onto such functions, in order to quantify how changes in quantiles are driven by changes in the first four statistical moments. Crucially, slopes in the proposed polynomials are orthogonal to each other by construction, allowing us to decouple different sources of distributional changes. Here, we present the three main steps in the framework: (a) quantile regression, (b) projection onto polynomials, and (c) statistical significance test. A schematic of the proposed framework is presented in Figure 1.

Figure 1. Schematic of the proposed framework illustrated using a synthetic time series. We generate a time series
![]() $ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
sampled from a time-dependent Beta distribution
$ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
sampled from a time-dependent Beta distribution
![]() $ P\left(s,t\right) $
(see Section 3.4). Temporal changes in statistical moments are computed analytically a priori and are chosen to come solely from the variance (second moment) and kurtosis (fourth moment). Step (a): we apply quantile regression for the range of quantiles
$ P\left(s,t\right) $
(see Section 3.4). Temporal changes in statistical moments are computed analytically a priori and are chosen to come solely from the variance (second moment) and kurtosis (fourth moment). Step (a): we apply quantile regression for the range of quantiles
![]() $ {q}_p $
, with
$ {q}_p $
, with
![]() $ p\in \left[\mathrm{0.05,0.95}\right] $
every
$ p\in \left[\mathrm{0.05,0.95}\right] $
every
![]() $ dp=0.05 $
for a total of
$ dp=0.05 $
for a total of
![]() $ 19 $
slopes. In panel (a), we show the quantile regression for
$ 19 $
slopes. In panel (a), we show the quantile regression for
![]() $ p=\mathrm{0.95,0.5} $
and 0.05. Note that
$ p=\mathrm{0.95,0.5} $
and 0.05. Note that
![]() $ q=q(p) $
and
$ q=q(p) $
and
![]() $ {q}_p $
is used only for convenience. Step (b): we project the 19 quantile slopes onto a set of four orthogonal polynomials (see panel b.3). Step (c): we quantify the statistical significance of coefficients
$ {q}_p $
is used only for convenience. Step (b): we project the 19 quantile slopes onto a set of four orthogonal polynomials (see panel b.3). Step (c): we quantify the statistical significance of coefficients
![]() $ \frac{dm_i}{dt} $
quantifying how independent changes in moments explain changes in quantiles computed in step (a) (
$ \frac{dm_i}{dt} $
quantifying how independent changes in moments explain changes in quantiles computed in step (a) (
![]() $ \frac{dm_i}{dt} $
; with
$ \frac{dm_i}{dt} $
; with
![]() $ i\in \left[1,4\right] $
representing changes in mean, variance, skewness, and kurtosis, respectively). Note that in Section 3.3 we refer to
$ i\in \left[1,4\right] $
representing changes in mean, variance, skewness, and kurtosis, respectively). Note that in Section 3.3 we refer to
![]() $ \frac{dm_i}{dt} $
as
$ \frac{dm_i}{dt} $
as
![]() $ {a}_i $
to simplify the notation. Significant changes at the 95% level come for this synthetic time series solely from the second and fourth moments, as known from analytical results. Additional synthetic tests are presented in Section 3.4.
$ {a}_i $
to simplify the notation. Significant changes at the 95% level come for this synthetic time series solely from the second and fourth moments, as known from analytical results. Additional synthetic tests are presented in Section 3.4.
3.1. Quantile regression
A quantile function
![]() $ {Q}_X(p),p\in \left[0,1\right] $
, of a random variable
$ {Q}_X(p),p\in \left[0,1\right] $
, of a random variable
![]() $ X $
returns a value
$ X $
returns a value
![]() $ x $
such that
$ x $
such that
![]() $ \left(p\times 100\right)\% $
of the values are less than
$ \left(p\times 100\right)\% $
of the values are less than
![]() $ x $
. For example, the 0.95 quantile
$ x $
. For example, the 0.95 quantile
![]() $ {Q}_X(0.95) $
is a real number
$ {Q}_X(0.95) $
is a real number
![]() $ x $
such that 95% of the values of the random variable,
$ x $
such that 95% of the values of the random variable,
![]() $ X $
, are smaller than
$ X $
, are smaller than
![]() $ x $
.
$ x $
.
![]() $ {Q}_X(p),p\in \left[0,1\right] $
is the inverse
$ {Q}_X(p),p\in \left[0,1\right] $
is the inverse
![]() $ {F}_X^{-1}(p) $
of the cumulative distribution function
$ {F}_X^{-1}(p) $
of the cumulative distribution function
![]() $ {F}_X(x)=P\left(X\le x\right)=p $
, representing the probability
$ {F}_X(x)=P\left(X\le x\right)=p $
, representing the probability
![]() $ p $
that
$ p $
that
![]() $ X $
would take a value less than or equal to
$ X $
would take a value less than or equal to
![]() $ x $
. In what follows, we simplify the notation and refer to
$ x $
. In what follows, we simplify the notation and refer to
![]() $ {Q}_X(p) $
as
$ {Q}_X(p) $
as
![]() $ {q}_p $
and to cumulative functions as
$ {q}_p $
and to cumulative functions as
![]() $ F(x) $
.
$ F(x) $
.
Quantile regression allows us to estimate temporal changes in the conditional median (i.e.,
![]() $ {q}_{0.5} $
) or any other quantile of a time-dependent distribution (Koenker and Bassett, Reference Koenker and Bassett1978; Koenker and Hallock, Reference Koenker and Hallock2001). Here, we focus on the case of linear regression. For each quantile,
$ {q}_{0.5} $
) or any other quantile of a time-dependent distribution (Koenker and Bassett, Reference Koenker and Bassett1978; Koenker and Hallock, Reference Koenker and Hallock2001). Here, we focus on the case of linear regression. For each quantile,
![]() $ {q}_p $
, we need to fit two parameters: an intercept
$ {q}_p $
, we need to fit two parameters: an intercept
![]() $ {\beta}_0\left({q}_p\right) $
and a slope
$ {\beta}_0\left({q}_p\right) $
and a slope
![]() $ {\beta}_1\left({q}_p\right) $
(see Figure 1). Differently from linear regression for which we minimize the mean square error, the quantile regression process places asymmetric weights on positive and negative residuals (Koenker and Hallock, Reference Koenker and Hallock2001).
$ {\beta}_1\left({q}_p\right) $
(see Figure 1). Differently from linear regression for which we minimize the mean square error, the quantile regression process places asymmetric weights on positive and negative residuals (Koenker and Hallock, Reference Koenker and Hallock2001).
Formally, given
![]() $ n $
observations at times
$ n $
observations at times
![]() $ {t}_i $
, written as
$ {t}_i $
, written as
![]() $ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
, and the assumption of linear relationship for each quantile
$ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
, and the assumption of linear relationship for each quantile
![]() $ {q}_p(t),p\,\in\,\left[0,1\right] $
, then the goal is to minimize the following cost function:
$ {q}_p(t),p\,\in\,\left[0,1\right] $
, then the goal is to minimize the following cost function:
 $$ \underset{\beta_0\left({q}_p\right),{\beta}_1\left({q}_p\right)\in \mathrm{\mathbb{R}}}{\arg \min}\sum \limits_{i=1}^n{\rho}_p\left({s}_i-{\beta}_0\left({q}_p\right)-{\beta}_1\left({q}_p\right)\hskip0.1em {t}_i\right), $$
$$ \underset{\beta_0\left({q}_p\right),{\beta}_1\left({q}_p\right)\in \mathrm{\mathbb{R}}}{\arg \min}\sum \limits_{i=1}^n{\rho}_p\left({s}_i-{\beta}_0\left({q}_p\right)-{\beta}_1\left({q}_p\right)\hskip0.1em {t}_i\right), $$
where the “check function”
![]() $ {\rho}_p(u)=p\max \left(u,0\right)+\left(1-p\right)\max \left(-u,0\right) $
, with
$ {\rho}_p(u)=p\max \left(u,0\right)+\left(1-p\right)\max \left(-u,0\right) $
, with
![]() $ p\,\in\,\left[0,1\right] $
, assigns asymmetric weights to residuals. For a given time series, we apply quantile regression for the range of quantiles
$ p\,\in\,\left[0,1\right] $
, assigns asymmetric weights to residuals. For a given time series, we apply quantile regression for the range of quantiles
![]() $ {q}_p $
with
$ {q}_p $
with
![]() $ p\,\in\,\left[\mathrm{0.05,0.95}\right] $
every
$ p\,\in\,\left[\mathrm{0.05,0.95}\right] $
every
![]() $ dp=0.05 $
for a total of 19 slopes (as done in McKinnon et al., Reference McKinnon, Rhines, Tingley and Huybers2016). This number of slope was found to be sufficient to discover the right changes in moments, as shown later on in the next section. An example of quantile regression for
$ dp=0.05 $
for a total of 19 slopes (as done in McKinnon et al., Reference McKinnon, Rhines, Tingley and Huybers2016). This number of slope was found to be sufficient to discover the right changes in moments, as shown later on in the next section. An example of quantile regression for
![]() $ p=\mathrm{0.95,0.5} $
and
$ p=\mathrm{0.95,0.5} $
and
![]() $ 0.05 $
is shown in Figure 1a.
$ 0.05 $
is shown in Figure 1a.
In practice, quantile regression studies depend on the existence of very fast algorithms (Chernozhukov et al., Reference Chernozhukov, Fernàndez-Val and Melly2022). Portnoy and Koenker (Reference Portnoy and Koenker1997) proposed a precise and time-efficient minimization method based on the Frisch–Newton algorithm. However, the computation time is still rather long in the case of multiple quantile regressions and bootstrap inference. To this end, very recently Chernozhukov et al. (Reference Chernozhukov, Fernàndez-Val and Melly2022) showed that the computation of many quantile regressions can be (vastly) accelerated by exploiting nearby quantile solutions. This method was essential for the completion of our work, especially when analyzing the climate model outputs, which included 12,636 time series each with 36,500 time steps. The algorithm can be found in the quantile regression package “quantreg” implemented in R as “quantile regression fitting via interior point methods” (i.e., method pfnb) (Koenker, Reference Koenker2022). In the case of sea level, each quantile
![]() $ {q}_p $
has dimensionality of
$ {q}_p $
has dimensionality of
![]() $ \left[{q}_p\right]=\left[\mathrm{length}\right] $
, so that the slopes have dimensions of
$ \left[{q}_p\right]=\left[\mathrm{length}\right] $
, so that the slopes have dimensions of
![]() $ \left[{\beta}_1\left({q}_p\right)\right]=\left[\frac{\mathrm{length}}{\mathrm{time}}\right] $
.
$ \left[{\beta}_1\left({q}_p\right)\right]=\left[\frac{\mathrm{length}}{\mathrm{time}}\right] $
.
3.2. Linking changes in quantiles to changes in statistical moments
The quantile regression step allows us to quantify slopes in
![]() $ N $
quantiles. This quantification can come at the expense of interpretability, especially when
$ N $
quantiles. This quantification can come at the expense of interpretability, especially when
![]() $ N $
is large and when analyzing more than one time series. To facilitate analysis and interpretation, we quantify how changes in quantiles of a distribution are driven by changes in the mean, variance, skewness, and kurtosis, therefore defining a single framework to study changes in quantiles and moments. All throughout the paper, we refer to the mean, variance, skewness, and kurtosis as
$ N $
is large and when analyzing more than one time series. To facilitate analysis and interpretation, we quantify how changes in quantiles of a distribution are driven by changes in the mean, variance, skewness, and kurtosis, therefore defining a single framework to study changes in quantiles and moments. All throughout the paper, we refer to the mean, variance, skewness, and kurtosis as
![]() $ \left({m}_1,{m}_2,{m}_3,{m}_4\right) $
for practical convenience and report their mathematical expression in Appendix C. A possible way to link changes in quantile to changes in moments was proposed in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016). The authors empirically derived a set of polynomials by observing how quantiles of a distribution change when changing its moments one at a time. The lack of orthogonality of such functions motivated the authors to adopt Legendre polynomials, which are orthogonal by construction and share similar shapes to the derived functions. Inspired by McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016), here we approach the problem from a theoretical point of view. We take advantage of the work of Cornish and Fisher (Reference Cornish and Fisher1937) and define a unified framework useful to study and explore temporal changes in both quantiles and moments of a distribution.
$ \left({m}_1,{m}_2,{m}_3,{m}_4\right) $
for practical convenience and report their mathematical expression in Appendix C. A possible way to link changes in quantile to changes in moments was proposed in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016). The authors empirically derived a set of polynomials by observing how quantiles of a distribution change when changing its moments one at a time. The lack of orthogonality of such functions motivated the authors to adopt Legendre polynomials, which are orthogonal by construction and share similar shapes to the derived functions. Inspired by McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016), here we approach the problem from a theoretical point of view. We take advantage of the work of Cornish and Fisher (Reference Cornish and Fisher1937) and define a unified framework useful to study and explore temporal changes in both quantiles and moments of a distribution.
3.2.1. Stationary process
The starting point of our derivation is the Cornish–Fisher expansion (Cornish and Fisher, Reference Cornish and Fisher1937; Wallace, Reference Wallace1958; Fisher and Cornish, Reference Fisher and Cornish1960; Hill and Davis, Reference Hill and Davis1968). Cornish and Fisher (Reference Cornish and Fisher1937) derived an asymptotic expansion expressing any quantile of a distribution as a function of its cumulants.Footnote 1 Studies often focus on a modified version written in terms of the first four distributional moments. Furthermore, in practical applications higher order moments show large sensitivity to sampling fluctuations, and Bekki et al. (Reference Bekki, Fowler, Mackulak and Nelson2009) showed that a fourth-order truncation often allows for very accurate estimations of quantiles.
Given a stationary distribution with mean
![]() $ {m}_1 $
, variance
$ {m}_1 $
, variance
![]() $ {m}_2 $
, skewness
$ {m}_2 $
, skewness
![]() $ {m}_3 $
, and excess kurtosis
$ {m}_3 $
, and excess kurtosis
![]() $ {m}_4 $
parameters, the following asymptotic relation holds (Cornish and Fisher, Reference Cornish and Fisher1937; Bekki et al., Reference Bekki, Fowler, Mackulak and Nelson2009):
$ {m}_4 $
parameters, the following asymptotic relation holds (Cornish and Fisher, Reference Cornish and Fisher1937; Bekki et al., Reference Bekki, Fowler, Mackulak and Nelson2009):
where
![]() $ {q}_p $
is the quantile of the “true” distribution and
$ {q}_p $
is the quantile of the “true” distribution and
![]() $ {z}_p $
is the quantile of a standard normal
$ {z}_p $
is the quantile of a standard normal
![]() $ \mathcal{N}\left(0,1\right) $
at
$ \mathcal{N}\left(0,1\right) $
at
![]() $ p\in \left[0,1\right] $
.Footnote 2 In other words,
$ p\in \left[0,1\right] $
.Footnote 2 In other words,
![]() $ {z}_p $
is the inverse
$ {z}_p $
is the inverse
![]() $ {F}^{-1}(p) $
of the cumulative distribution
$ {F}^{-1}(p) $
of the cumulative distribution
![]() $ F(x)={\left(2\pi \right)}^{-1/2}{\int}_{-\infty}^x\exp \left(-{\upsilon}^2/2\right) d\upsilon $
of a Gaussian distribution with zero mean and unit variance. Importantly,
$ F(x)={\left(2\pi \right)}^{-1/2}{\int}_{-\infty}^x\exp \left(-{\upsilon}^2/2\right) d\upsilon $
of a Gaussian distribution with zero mean and unit variance. Importantly,
![]() $ {q}_p $
,
$ {q}_p $
,
![]() $ {m}_1 $
, and
$ {m}_1 $
, and
![]() $ \sqrt{m_2} $
have the same dimension, whereas
$ \sqrt{m_2} $
have the same dimension, whereas
![]() $ {z}_p $
,
$ {z}_p $
,
![]() $ {m}_3 $
, and
$ {m}_3 $
, and
![]() $ {m}_4 $
are nondimensional. A synthetic and a first climate-related test are discussed in Appendix D.
$ {m}_4 $
are nondimensional. A synthetic and a first climate-related test are discussed in Appendix D.
In the case of a normal distributions,
![]() $ {m}_3={m}_4=0 $
and the expansion (3) reduces to
$ {m}_3={m}_4=0 $
and the expansion (3) reduces to
![]() $ {q}_p={m}_1+\sqrt{m_2}\hskip0.1em {z}_p $
. The inclusion of the third and fourth moments,
$ {q}_p={m}_1+\sqrt{m_2}\hskip0.1em {z}_p $
. The inclusion of the third and fourth moments,
![]() $ {m}_3 $
and
$ {m}_3 $
and
![]() $ {m}_4 $
, allows us to approximate any quantile of a nonnormal distribution as a function of a normal (Gaussian) distribution. This formula is a powerful tool as it can provide asymptotic estimations of arbitrarily large quantiles, otherwise difficult from data alone. It is useful for distributions that do not show large differences from a normal distribution with the domain of validity further discussed by Maillard (Reference Maillard2012) and Amédée-Manesme et al. (Reference Amédée-Manesme, Barthélémy and Maillard2019).
$ {m}_4 $
, allows us to approximate any quantile of a nonnormal distribution as a function of a normal (Gaussian) distribution. This formula is a powerful tool as it can provide asymptotic estimations of arbitrarily large quantiles, otherwise difficult from data alone. It is useful for distributions that do not show large differences from a normal distribution with the domain of validity further discussed by Maillard (Reference Maillard2012) and Amédée-Manesme et al. (Reference Amédée-Manesme, Barthélémy and Maillard2019).
3.2.2. Nonstationary process
Here, we aim to understand and quantify how temporal changes in individual quantiles are driven by changes in statistical moments. In theory, each quantile
![]() $ {q}_p $
is time dependent through all moments of the distribution. Here, we consider dependence only up to the first four moments:
$ {q}_p $
is time dependent through all moments of the distribution. Here, we consider dependence only up to the first four moments:
Here,
![]() $ {m}_1,{m}_2,{m}_3 $
, and
$ {m}_1,{m}_2,{m}_3 $
, and
![]() $ {m}_4 $
refer to the mean, variance, skewness, and excess kurtosis. We focus on linear changes in time and therefore write
$ {m}_4 $
refer to the mean, variance, skewness, and excess kurtosis. We focus on linear changes in time and therefore write
 $$ \frac{dq_p}{dt}=\frac{\partial {q}_p}{\partial {m}_1}\frac{dm_1}{dt}+\frac{\partial {q}_p}{\partial {m}_2}\frac{dm_2}{dt}+\frac{\partial {q}_p}{\partial {m}_3}\frac{dm_3}{dt}+\frac{\partial {q}_p}{\partial {m}_4}\frac{dm_4}{dt}=\sum \limits_{i=1}^4\frac{\partial {q}_p}{\partial {m}_i}\frac{dm_i}{dt}. $$
$$ \frac{dq_p}{dt}=\frac{\partial {q}_p}{\partial {m}_1}\frac{dm_1}{dt}+\frac{\partial {q}_p}{\partial {m}_2}\frac{dm_2}{dt}+\frac{\partial {q}_p}{\partial {m}_3}\frac{dm_3}{dt}+\frac{\partial {q}_p}{\partial {m}_4}\frac{dm_4}{dt}=\sum \limits_{i=1}^4\frac{\partial {q}_p}{\partial {m}_i}\frac{dm_i}{dt}. $$
Each term
![]() $ \frac{\partial {q}_p}{\partial {m}_i} $
in Eq. (5) can be further evaluated by differentiating Eq. (3):
$ \frac{\partial {q}_p}{\partial {m}_i} $
in Eq. (5) can be further evaluated by differentiating Eq. (3):
 $$ \left\{\begin{array}{l}\frac{\partial {q}_p}{\partial {m}_1}=1\\ {}\frac{\partial {q}_p}{\partial {m}_2}=\frac{1}{2}\frac{1}{\sqrt{m_2}}\left[{z}_p+\frac{1}{6}\left({z}_p^2-1\right)\hskip0.1em {m}_3-\frac{1}{36}\left(2{z}_p^3-5{z}_p\right)\hskip0.1em {m}_3^2+\frac{1}{24}\left({z}_p^3-3{z}_p\right)\hskip0.1em {m}_4\right]\\ {}\frac{\partial {q}_p}{\partial {m}_3}=\sqrt{m_2}\hskip0.1em \left[\frac{1}{6}\left({z}_p^2-1\right)-\frac{1}{18}\left(2{z}_p^3-5{z}_p\right)\hskip0.1em {m}_3\right]\\ {}\frac{\partial {q}_p}{\partial {m}_4}=\frac{\sqrt{m_2}}{24}\left({z}_p^3-3{z}_p\right).\end{array}\right. $$
$$ \left\{\begin{array}{l}\frac{\partial {q}_p}{\partial {m}_1}=1\\ {}\frac{\partial {q}_p}{\partial {m}_2}=\frac{1}{2}\frac{1}{\sqrt{m_2}}\left[{z}_p+\frac{1}{6}\left({z}_p^2-1\right)\hskip0.1em {m}_3-\frac{1}{36}\left(2{z}_p^3-5{z}_p\right)\hskip0.1em {m}_3^2+\frac{1}{24}\left({z}_p^3-3{z}_p\right)\hskip0.1em {m}_4\right]\\ {}\frac{\partial {q}_p}{\partial {m}_3}=\sqrt{m_2}\hskip0.1em \left[\frac{1}{6}\left({z}_p^2-1\right)-\frac{1}{18}\left(2{z}_p^3-5{z}_p\right)\hskip0.1em {m}_3\right]\\ {}\frac{\partial {q}_p}{\partial {m}_4}=\frac{\sqrt{m_2}}{24}\left({z}_p^3-3{z}_p\right).\end{array}\right. $$
We assume relatively small deviation from Gaussian behavior and focus only on first-order changes in Eq. (6). This is a reasonable assumption as the dynamics of many climate observables often show a strong Gaussian component, especially when focusing on anomalies (after removing climatologies). In case of (relatively) large deviation from Gaussianity, the framework is still useful at first order as suggested by tests in Appendix D.1. In other words, we evaluate Eq. (6) locally at the point
![]() $ {m}_{\ast }=\left({m}_1=0,{m}_2=1,{m}_3=0,{m}_4=0\right) $
to describe changes in the neighborhood of a Gaussian distribution. Therefore, we relate the slopes
$ {m}_{\ast }=\left({m}_1=0,{m}_2=1,{m}_3=0,{m}_4=0\right) $
to describe changes in the neighborhood of a Gaussian distribution. Therefore, we relate the slopes
![]() $ {\beta}_1\left({q}_p\right) $
computed in the quantile regression step in Eq. (2) to changes in moments as:
$ {\beta}_1\left({q}_p\right) $
computed in the quantile regression step in Eq. (2) to changes in moments as:
 $$ {\beta}_1\left({q}_p\right)\sim {\left.\frac{dq_p}{dt}\right|}_{m_{\ast }}={\left.\sum \limits_{i=1}^4\frac{dm_i}{dt}\frac{\partial {q}_p}{\partial {m}_i}\right|}_{m_{\ast }}=\sum \limits_{i=1}^4\frac{dm_i}{dt}{b}_i(p). $$
$$ {\beta}_1\left({q}_p\right)\sim {\left.\frac{dq_p}{dt}\right|}_{m_{\ast }}={\left.\sum \limits_{i=1}^4\frac{dm_i}{dt}\frac{\partial {q}_p}{\partial {m}_i}\right|}_{m_{\ast }}=\sum \limits_{i=1}^4\frac{dm_i}{dt}{b}_i(p). $$
Here, the set of polynomials,
![]() $ {b}_i(p) $
, are defined by evaluating the terms
$ {b}_i(p) $
, are defined by evaluating the terms
![]() $ \frac{\partial {q}_p}{\partial {m}_i} $
;
$ \frac{\partial {q}_p}{\partial {m}_i} $
;
![]() $ i\,\in\,\left[1,4\right] $
in Eq. (6) in the point
$ i\,\in\,\left[1,4\right] $
in Eq. (6) in the point
![]() $ {m}_{\ast }=\left({m}_1=0,{m}_2=1,{m}_3=0,{m}_4=0\right) $
:
$ {m}_{\ast }=\left({m}_1=0,{m}_2=1,{m}_3=0,{m}_4=0\right) $
:
 $$ \left\{\begin{array}{ll}{\left.{b}_1(p)=\frac{\partial {q}_p}{\partial {m}_1}\right|}_{m_{\ast }}& =1\\ {}{\left.{b}_2(p)=\frac{\partial {q}_p}{\partial {m}_2}\right|}_{m_{\ast }}& =\frac{z_p}{2}\\ {}{\left.{b}_3(p)=\frac{\partial {q}_p}{\partial {m}_3}\right|}_{m_{\ast }}& =\frac{1}{6}\left({z}_p^2-1\right)\\ {}{\left.{b}_4(p)=\frac{\partial {q}_p}{\partial {m}_4}\right|}_{m_{\ast }}& =\frac{1}{24}\left({z}_p^3-3{z}_p\right).\end{array}\right. $$
$$ \left\{\begin{array}{ll}{\left.{b}_1(p)=\frac{\partial {q}_p}{\partial {m}_1}\right|}_{m_{\ast }}& =1\\ {}{\left.{b}_2(p)=\frac{\partial {q}_p}{\partial {m}_2}\right|}_{m_{\ast }}& =\frac{z_p}{2}\\ {}{\left.{b}_3(p)=\frac{\partial {q}_p}{\partial {m}_3}\right|}_{m_{\ast }}& =\frac{1}{6}\left({z}_p^2-1\right)\\ {}{\left.{b}_4(p)=\frac{\partial {q}_p}{\partial {m}_4}\right|}_{m_{\ast }}& =\frac{1}{24}\left({z}_p^3-3{z}_p\right).\end{array}\right. $$
Such functions are scaled Hermite polynomials of the function
![]() $ {z}_p $
and defined in the range
$ {z}_p $
and defined in the range
![]() $ p\,\in\,\left[0,1\right] $
. The polynomials in Eq. (8) satisfy
$ p\,\in\,\left[0,1\right] $
. The polynomials in Eq. (8) satisfy
 $$ {\int}_0^1{b}_i(p){b}_j(p) dp=0\hskip1em \mathrm{if}i\ne j, $$
$$ {\int}_0^1{b}_i(p){b}_j(p) dp=0\hskip1em \mathrm{if}i\ne j, $$
and so they are orthogonal to each other. We depict these four functions in Figure 1b.Footnote 3
Eq. (7) allows us to examine how time changes in distributional quantiles are driven by time changes in the first four moments. We note that apart from
![]() $ {b}_1(p) $
, all polynomials in Eq. (8) differ from the ones in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016). As an example, an important difference is in the
$ {b}_1(p) $
, all polynomials in Eq. (8) differ from the ones in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016). As an example, an important difference is in the
![]() $ {b}_2(p) $
function, quantifying changes in variance. In the case of a drifting Gaussian distribution,
$ {b}_2(p) $
function, quantifying changes in variance. In the case of a drifting Gaussian distribution,
![]() $ {b}_2(p) $
quantifies the exact link between changes in moments and quantiles. In the “bulk” of the distribution, the function
$ {b}_2(p) $
quantifies the exact link between changes in moments and quantiles. In the “bulk” of the distribution, the function
![]() $ {b}_2(p) $
derived in Eq. (8) gives negative(positive) corrections to the correspondent function in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) for
$ {b}_2(p) $
derived in Eq. (8) gives negative(positive) corrections to the correspondent function in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) for
![]() $ p $
greater (smaller) than
$ p $
greater (smaller) than
![]() $ p=0.5 $
. Furthermore,
$ p=0.5 $
. Furthermore,
![]() $ {b}_2(p) $
shows how changes in variance also drive changes in distributional tails, with quantiles diverging to
$ {b}_2(p) $
shows how changes in variance also drive changes in distributional tails, with quantiles diverging to
![]() $ +\infty \left(-\infty \right) $
when
$ +\infty \left(-\infty \right) $
when
![]() $ p\to (1)0 $
.
$ p\to (1)0 $
.
The slopes
![]() $ {\beta}_1\left({q}_p\right) $
appearing in Eq. (7) can be efficiently estimated through the quantile regression step as shown in Eq. (2). The polynomials
$ {\beta}_1\left({q}_p\right) $
appearing in Eq. (7) can be efficiently estimated through the quantile regression step as shown in Eq. (2). The polynomials
![]() $ {b}_i(p) $
have been derived in Eq. (8) and follow from Cornish and Fisher (Reference Cornish and Fisher1937). Therefore, changes in moments,
$ {b}_i(p) $
have been derived in Eq. (8) and follow from Cornish and Fisher (Reference Cornish and Fisher1937). Therefore, changes in moments,
![]() $ \frac{dm_i}{dt} $
, can be computed as the least-squares solution of Eq. (7). An example is shown in Figure 1b for a Beta distribution with changes coming exclusively from variance and kurtosis (i.e.,
$ \frac{dm_i}{dt} $
, can be computed as the least-squares solution of Eq. (7). An example is shown in Figure 1b for a Beta distribution with changes coming exclusively from variance and kurtosis (i.e.,
![]() $ {m}_2 $
and
$ {m}_2 $
and
![]() $ {m}_4 $
).
$ {m}_4 $
).
![]() $ \frac{dm_1}{dt} $
is equivalent to a linear regression. We refer to the coefficients
$ \frac{dm_1}{dt} $
is equivalent to a linear regression. We refer to the coefficients
![]() $ \frac{dm_i}{dt} $
as changes (or slopes) in moments. However, such inferred changes are orthogonal to each other, and this property may not be the case for changes in the true moments. The orthogonality constraint offers a useful and interpretable way to decompose independent sources of shifts in a distribution.
$ \frac{dm_i}{dt} $
as changes (or slopes) in moments. However, such inferred changes are orthogonal to each other, and this property may not be the case for changes in the true moments. The orthogonality constraint offers a useful and interpretable way to decompose independent sources of shifts in a distribution.
In the case of sea level, the dimensionality in changes in moments
![]() $ \frac{dm_i}{dt} $
;
$ \frac{dm_i}{dt} $
;
![]() $ i\,\in\,\left[1,4\right] $
is as follows:
$ i\,\in\,\left[1,4\right] $
is as follows:
![]() $ \left[\frac{dm_1}{dt}\right]=\left[\frac{\mathrm{length}}{\mathrm{time}}\right],\left[\frac{dm_2}{dt}\right]=\left[\frac{{\mathrm{length}}^2}{\mathrm{time}}\right],\left[\frac{dm_3}{dt}\right]=\left[\frac{1}{\mathrm{time}}\right],\frac{dm_4}{dt}=\left[\frac{1}{\mathrm{time}}\right] $
.
$ \left[\frac{dm_1}{dt}\right]=\left[\frac{\mathrm{length}}{\mathrm{time}}\right],\left[\frac{dm_2}{dt}\right]=\left[\frac{{\mathrm{length}}^2}{\mathrm{time}}\right],\left[\frac{dm_3}{dt}\right]=\left[\frac{1}{\mathrm{time}}\right],\frac{dm_4}{dt}=\left[\frac{1}{\mathrm{time}}\right] $
.
3.3. Statistical significance
The significance test is performed via the bootstrapping methodology (Chernick et al., Reference Chernick, González-Manteiga, Crujeiras, Barrios and Lovric2011). For a given dataset (i.e., model’s output or tide gauges), we consider the
![]() $ j $
-th time series,
$ j $
-th time series,
![]() $ {x}_j(t) $
, and estimate the statistical significance of each coefficient
$ {x}_j(t) $
, and estimate the statistical significance of each coefficient
![]() $ {a}_i=\frac{dm_i}{dt} $
,
$ {a}_i=\frac{dm_i}{dt} $
,
![]() $ i\,\in\,\left[1,4\right] $
. We do so by permuting (with replacement)
$ i\,\in\,\left[1,4\right] $
. We do so by permuting (with replacement)
![]() $ {x}_j(t) $
$ {x}_j(t) $
![]() $ B $
times and recomputing the slopes in moments
$ B $
times and recomputing the slopes in moments
![]() $ {a}_i $
at each iteration. We choose a value of
$ {a}_i $
at each iteration. We choose a value of
![]() $ B=1000 $
and show the sensitivity of such a choice for one time series in Figure F2 (results do not change on average for randomly chosen time series). This method allows to construct a distribution approximating the null distribution under the null hypothesis of stationarity. For this resampling approach, we use block-bootstrapping, with blocks of one season to satisfy the assumption of statistical independence required in the bootstrapping test (Chernick et al., Reference Chernick, González-Manteiga, Crujeiras, Barrios and Lovric2011). The robustness on this choice of block size is mentioned in Section 4 and detailed in Appendix B. The specific block-bootstrapping considered is the moving block-bootstrapping that allows for overlapping blocks as described in Künsch (Reference Künsch1989).
$ B=1000 $
and show the sensitivity of such a choice for one time series in Figure F2 (results do not change on average for randomly chosen time series). This method allows to construct a distribution approximating the null distribution under the null hypothesis of stationarity. For this resampling approach, we use block-bootstrapping, with blocks of one season to satisfy the assumption of statistical independence required in the bootstrapping test (Chernick et al., Reference Chernick, González-Manteiga, Crujeiras, Barrios and Lovric2011). The robustness on this choice of block size is mentioned in Section 4 and detailed in Appendix B. The specific block-bootstrapping considered is the moving block-bootstrapping that allows for overlapping blocks as described in Künsch (Reference Künsch1989).
We consider the following two significance tests.
-
1. When dealing with one or few time series, we consider a two-tailed test and deem slopes as significant at level
 $ \alpha $
if in the
$ \alpha $
if in the
 $ \left(1-\frac{\alpha }{2}\right)\% $
(or
$ \left(1-\frac{\alpha }{2}\right)\% $
(or
 $ \frac{\alpha }{2}\% $
) of the upper (or lower) tails of the bootstrapped distribution. We choose
$ \frac{\alpha }{2}\% $
) of the upper (or lower) tails of the bootstrapped distribution. We choose
 $ \alpha =0.05 $
(i.e., 95% significance level).
$ \alpha =0.05 $
(i.e., 95% significance level). -
2. When considering many time series, we face a multiple testing problem and more and more false positives are expected in the statistical inference (James et al., Reference James, Witten, Hastie and Tibshirani2013. To control the ratio of false positives, we adopt the false discovery rate (FDR) test proposed by Benjamini and Hochberg (Reference Benjamini and Hochberg1995). For a given time series
 $ {x}_j(t) $
and a corresponding slope
$ {x}_j(t) $
and a corresponding slope
 $ {a}_i $
,
$ {a}_i $
,
 $ i\,\in\,\left[1,4\right] $
, we compute a p-value pi. We perform this computation for all
$ i\,\in\,\left[1,4\right] $
, we compute a p-value pi. We perform this computation for all
 $ M $
time series in the dataset under investigation. We then rank all
$ M $
time series in the dataset under investigation. We then rank all
 $ M $
p-values in the ascending order and keep only the first
$ M $
p-values in the ascending order and keep only the first
 $ m<M $
so that
$ m<M $
so that
 $ {p}_m $
is the largest p-value such that
$ {p}_m $
is the largest p-value such that
 $ {p}_m<\phi \frac{m}{M} $
, where
$ {p}_m<\phi \frac{m}{M} $
, where
 $ \phi $
is the FDR. Note that the FDR is usually denoted by the letter “
$ \phi $
is the FDR. Note that the FDR is usually denoted by the letter “
 $ q $
”. Here, we use
$ q $
”. Here, we use
 $ \phi $
to avoid confusions with quantiles
$ \phi $
to avoid confusions with quantiles
 $ q $
in the quantile regression step. In plain words, a FDR of 10% would imply that no more than
$ q $
in the quantile regression step. In plain words, a FDR of 10% would imply that no more than
 $ 10\% $
of the rejected null hypotheses are false positives. This method has been shown to be an efficient test to control on average the ratio of false positives arising from multiple testing (Benjamini and Hochberg, Reference Benjamini and Hochberg1995) and found applications in climate science (Ventura et al., Reference Ventura, Paciorek and Risbey2004; Wilks, Reference Wilks2006; Fountalis et al., Reference Fountalis, Dovrolis, Bracco, Dilkina and Keilholz2018; Runge et al., Reference Runge, Nowack, Kretschmer, Flaxman and Sejdinovic2019).
$ 10\% $
of the rejected null hypotheses are false positives. This method has been shown to be an efficient test to control on average the ratio of false positives arising from multiple testing (Benjamini and Hochberg, Reference Benjamini and Hochberg1995) and found applications in climate science (Ventura et al., Reference Ventura, Paciorek and Risbey2004; Wilks, Reference Wilks2006; Fountalis et al., Reference Fountalis, Dovrolis, Bracco, Dilkina and Keilholz2018; Runge et al., Reference Runge, Nowack, Kretschmer, Flaxman and Sejdinovic2019).
In our case, this step requires to approximate a p-value from a bootstrapped distribution. Given the
![]() $ j $
-th time series
$ j $
-th time series
![]() $ {x}_j(t) $
and a slope
$ {x}_j(t) $
and a slope
![]() $ {a}_i=\frac{dm_i}{dt} $
,
$ {a}_i=\frac{dm_i}{dt} $
,
![]() $ i\,\in\,\left[1,4\right] $
, we denote
$ i\,\in\,\left[1,4\right] $
, we denote
![]() $ {a}_i^{\ast 1},{a}_i^{\ast 2},\dots, {a}_i^{\ast B} $
as the
$ {a}_i^{\ast 1},{a}_i^{\ast 2},\dots, {a}_i^{\ast B} $
as the
![]() $ B $
bootstrapped slopes. We define the correspondent p-value of
$ B $
bootstrapped slopes. We define the correspondent p-value of
![]() $ {a}_i $
as
$ {a}_i $
as
![]() $ {p}_i=\frac{\sum_{b=1}^B{1}_{\mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid }}{B} $
, where
$ {p}_i=\frac{\sum_{b=1}^B{1}_{\mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid }}{B} $
, where
![]() $ {1}_{\mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid }=1 $
if
$ {1}_{\mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid }=1 $
if
![]() $ \mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid $
and zero otherwise (James et al., Reference James, Witten, Hastie and Tibshirani2013).
$ \mid {a}_i^{\ast b}\mid \ge \mid {a}_i\mid $
and zero otherwise (James et al., Reference James, Witten, Hastie and Tibshirani2013).
3.4. Synthetic tests
In this section, we test the proposed framework on two time-dependent distributions with known changes in moments. We consider two time-dependent processes sampled from a Gaussian and Beta distribution and display tests in Figure 2.
-
• We define a time-dependent Gaussian process
 $ P\left(x,t\right)=\frac{1}{\sqrt{2\pi bt}}{e}^{\frac{{\left(x- at\right)}^2}{2 bt}} $
defined over
$ P\left(x,t\right)=\frac{1}{\sqrt{2\pi bt}}{e}^{\frac{{\left(x- at\right)}^2}{2 bt}} $
defined over
 $ x\,\in\,\mathrm{\mathbb{R}} $
with mean
$ x\,\in\,\mathrm{\mathbb{R}} $
with mean
 $ {m}_1= at $
and variance
$ {m}_1= at $
and variance
 $ {m}_2= bt $
.
$ {m}_2= bt $
.
 $ a,b\,\in\,\mathrm{\mathbb{R}} $
and
$ a,b\,\in\,\mathrm{\mathbb{R}} $
and
 $ t $
represents the time vector. We choose
$ t $
represents the time vector. We choose
 $ a=b=5 $
. In this case, we expect distributional changes to be driven exclusively by the mean and variance.
$ a=b=5 $
. In this case, we expect distributional changes to be driven exclusively by the mean and variance. -
• We consider a stationary Beta distribution
 $ P(x)=\frac{x^{\alpha -1}{\left(1-x\right)}^{\beta -1}}{B\left(\alpha, \beta \right)} $
defined over
$ P(x)=\frac{x^{\alpha -1}{\left(1-x\right)}^{\beta -1}}{B\left(\alpha, \beta \right)} $
defined over
 $ x\,\in\,\left[0,1\right] $
. Here,
$ x\,\in\,\left[0,1\right] $
. Here,
 $ B\left(\alpha, \beta \right)=\frac{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\Gamma \left(\alpha +\beta \right)} $
, with
$ B\left(\alpha, \beta \right)=\frac{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\Gamma \left(\alpha +\beta \right)} $
, with
 $ \Gamma $
being the Gamma function (Davis, Reference Davis1959). Therefore,
$ \Gamma $
being the Gamma function (Davis, Reference Davis1959). Therefore,
 $ P(x) $
depends on two parameters,
$ P(x) $
depends on two parameters,
 $ \alpha $
and
$ \alpha $
and
 $ \beta $
, controlling the “thickness” of the tails of the distribution. A larger
$ \beta $
, controlling the “thickness” of the tails of the distribution. A larger
 $ \alpha $
(
$ \alpha $
(
 $ \beta $
) implies negative (positive) skewness; the distribution is symmetric if
$ \beta $
) implies negative (positive) skewness; the distribution is symmetric if
 $ \alpha =\beta $
. The mean, variance, skewness, and kurtosis read as:
$ \alpha =\beta $
. The mean, variance, skewness, and kurtosis read as:
 $$ \left\{\begin{array}{ll}{m}_1& =\frac{\alpha }{\alpha +\beta}\\ {}{m}_2& =\frac{\alpha \beta}{{\left(\alpha +\beta \right)}^2\left(1+\alpha +\beta \right)}\\ {}{m}_3& =\frac{2\left(\beta -\alpha \right)\sqrt{1+\alpha +\beta }}{\sqrt{\alpha}\sqrt{\beta}\left(2+\alpha +\beta \right)}\\ {}{m}_4& =\frac{3\left(1+\alpha +\beta \right)\left(\alpha \beta \left(\alpha +\beta -6\right)+2{\left(\alpha +\beta \right)}^2\right)}{\alpha \beta \left(2+\alpha +\beta \right)\left(3+\alpha +\beta \right)}.\end{array}\right. $$
$$ \left\{\begin{array}{ll}{m}_1& =\frac{\alpha }{\alpha +\beta}\\ {}{m}_2& =\frac{\alpha \beta}{{\left(\alpha +\beta \right)}^2\left(1+\alpha +\beta \right)}\\ {}{m}_3& =\frac{2\left(\beta -\alpha \right)\sqrt{1+\alpha +\beta }}{\sqrt{\alpha}\sqrt{\beta}\left(2+\alpha +\beta \right)}\\ {}{m}_4& =\frac{3\left(1+\alpha +\beta \right)\left(\alpha \beta \left(\alpha +\beta -6\right)+2{\left(\alpha +\beta \right)}^2\right)}{\alpha \beta \left(2+\alpha +\beta \right)\left(3+\alpha +\beta \right)}.\end{array}\right. $$

Figure 2. Testing the methodology on time series
![]() $ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
sampled from time-dependent Gaussian and Beta distributions
$ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
sampled from time-dependent Gaussian and Beta distributions
![]() $ P\left(s,t\right) $
. (a) Time series sampled from a time-dependent Gaussian distribution. (b) Linear quantile slopes for the time series shown in panel (a). The slopes
$ P\left(s,t\right) $
. (a) Time series sampled from a time-dependent Gaussian distribution. (b) Linear quantile slopes for the time series shown in panel (a). The slopes
![]() $ {\beta}_1\left({q}_p\right) $
are computed for
$ {\beta}_1\left({q}_p\right) $
are computed for
![]() $ p\in \left[\mathrm{0.05,0.95}\right] $
every
$ p\in \left[\mathrm{0.05,0.95}\right] $
every
![]() $ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c) Time series sampled from a time-dependent Beta distribution. (d) Same as panel (b) but for the case of the Beta distribution. In both cases, the method identifies the statistical moments driving changes in the distributions.
$ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c) Time series sampled from a time-dependent Beta distribution. (d) Same as panel (b) but for the case of the Beta distribution. In both cases, the method identifies the statistical moments driving changes in the distributions.
We then introduce a “drift” in this distribution by prescribing
![]() $ \alpha = at $
and
$ \alpha = at $
and
![]() $ \beta = bt $
and choose
$ \beta = bt $
and choose
![]() $ a=1 $
and
$ a=1 $
and
![]() $ b=2 $
. This defines a process with constant mean but time-dependent variance, skewness, and kurtosis. For these parameters, the exact moments are then
$ b=2 $
. This defines a process with constant mean but time-dependent variance, skewness, and kurtosis. For these parameters, the exact moments are then
![]() $ \left({m}_1,{m}_2,{m}_3,{m}_4\right)=\left(\frac{1}{3},\frac{2}{9+27t},\frac{\sqrt{2+6t}}{2+3t},3-\frac{3}{2+3t}\right) $
.
$ \left({m}_1,{m}_2,{m}_3,{m}_4\right)=\left(\frac{1}{3},\frac{2}{9+27t},\frac{\sqrt{2+6t}}{2+3t},3-\frac{3}{2+3t}\right) $
.
In both cases, we create a time-dependent process
![]() $ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
in the temporal range
$ \left\{\left({t}_1,{s}_1\right),\left({t}_2,{s}_2\right),\dots \right\} $
in the temporal range
![]() $ t\,\in\,\left[1,3\right] $
. In this temporal range, changes can be weakly nonlinear but still far from strong nonlinearities. Specifically, at each time step
$ t\,\in\,\left[1,3\right] $
. In this temporal range, changes can be weakly nonlinear but still far from strong nonlinearities. Specifically, at each time step
![]() $ dt={10}^{-4} $
we random sample from the two distributions
$ dt={10}^{-4} $
we random sample from the two distributions
![]() $ P\left(s,t\right) $
. We then apply the proposed framework to (a) estimate quantile slopes
$ P\left(s,t\right) $
. We then apply the proposed framework to (a) estimate quantile slopes
![]() $ {\beta}_1\left({q}_p\right) $
and (b) compute the respective changes in moments
$ {\beta}_1\left({q}_p\right) $
and (b) compute the respective changes in moments
![]() $ \frac{dm_i}{dt} $
. By random sampling at each
$ \frac{dm_i}{dt} $
. By random sampling at each
![]() $ dt $
, consecutive time steps are independent by definition and block sizes in the boostrapping procedure are equal to 1 time step. Results for the Gaussian and Beta distributions cases are shown in Figure 2. The method correctly identifies the statistical moments driving changes in the distributions. We note that the proposed linear framework is still valid in the presence of weak nonlinearities such as for
$ dt $
, consecutive time steps are independent by definition and block sizes in the boostrapping procedure are equal to 1 time step. Results for the Gaussian and Beta distributions cases are shown in Figure 2. The method correctly identifies the statistical moments driving changes in the distributions. We note that the proposed linear framework is still valid in the presence of weak nonlinearities such as for
![]() $ {m}_2,{m}_3 $
, and
$ {m}_2,{m}_3 $
, and
![]() $ {m}_4 $
for the process sampled from the Beta distribution.
$ {m}_4 $
for the process sampled from the Beta distribution.
Tests for a process with prescribed changes in only the variance,
![]() $ {m}_2 $
, and kurtosis,
$ {m}_2 $
, and kurtosis,
![]() $ {m}_4 $
, are shown in the schematic in Figure 1.
$ {m}_4 $
, are shown in the schematic in Figure 1.
4. Results
4.1. Changes in coastal sea level distributions from tide gauges
Changes in sea level distributions measured by tide gauges for the period 1970–2017 are summarized in Figure 3 and Table 1. The statistical significance test used is the FDR (see Section 3.3) with
![]() $ \phi =0.05 $
. The p-values are computed from the block-bootstrapped distributions (Section 3.3), and a sensitivity analysis on the chosen block-size is shown in Appendix E.
$ \phi =0.05 $
. The p-values are computed from the block-bootstrapped distributions (Section 3.3), and a sensitivity analysis on the chosen block-size is shown in Appendix E.

Figure 3. Projection onto mean, variance, skewness, and kurtosis polynomials for the period 1970–2017. Statistically significant changes are marked with filled “circles,” whereas insignificant changes are marked with “X”s. Statistical significance is computed using the FDR test with threshold
![]() $ \phi =0.05 $
.
$ \phi =0.05 $
.
Table 1. Percentage of significant coefficients for the FDR test.

Note. All figures report results obtained with the FDR test with a threshold
![]() $ \phi =0.05 $
(see Section 3.3).
$ \phi =0.05 $
(see Section 3.3).
The main significant changes in the observed coastal sea level distributions come from a shift in the mean. Contributions coming from higher order moments are less significant and sporadic (see Table 1). Among the 92 tide gauges with significant changes in the mean, the average slope is 2.08 mm/year (see Table 1). However, if only the positive significant slopes are considered (78 of the 92 tide gauges), then the slope increases to 2.92 mm/year.
Drivers of mean changes in tide gauges have been discussed in Wang et al. (Reference Wang, Church, Zhang, Gregory, Zanna and Chen2021), where the authors identified stereodynamic sea level changes (i.e., changes driven by currents, temperature, and salinity) as the main contributors of the observed trends. Large trends in the US east coast mainly come from the combined effect of sterodynamic and GIA contributions. Downward sea level trends are driven mainly by GIA (e.g., Baltic Sea [Weisse et al., Reference Weisse, Dailidiené, Hünicke, Kahma, Madsen, Omstedt, Parnell, Schöne, Soomere, Zhang and Zorita2021]), terrestrial water storage, or mass loss of land ice (e.g., Alaska coastline).
We further analyze tide gauges with (a) more than 80 years of data and (b) less than 20% of missing values, with results presented in Figure 4 and Table 1. The record spanned in such locations is reported in Appendix B. The significance test adopted is FDR. Also in this case, we observe significant changes in the distributional mean but not in higher order moments. As an exception, two records from Panama (i.e., Cristobal and Balboa) show a significant change in variance. Such changes can be partially explained by very large anomalous El Niño and La Niña events since 1980, as shown in Appendix E.

Figure 4. Projection onto mean, variance, skewness, and kurtosis functions. All tide gauges considered have a record longer than 80 years and less than 20
![]() $ \% $
of missing data. Statistically significant changes are marked with filled “circles,” whereas insignificant changes are marked with “X”s. Statistical significance is computed using the FDR test with threshold
$ \% $
of missing data. Statistically significant changes are marked with filled “circles,” whereas insignificant changes are marked with “X”s. Statistical significance is computed using the FDR test with threshold
![]() $ \phi =0.05 $
for the mean, variance, skewness, and kurtosis slopes. The starting and ending date for each tide gauge is shown in Appendix B.
$ \phi =0.05 $
for the mean, variance, skewness, and kurtosis slopes. The starting and ending date for each tide gauge is shown in Appendix B.
We conclude that, independently of the period analyzed, changes in tide gauge measured coastal sea level distributions can be characterized by a shift in the mean with no statistically significant change in shape.
4.2. GFDL-CM4 climate model
We quantify changes in sea level distributions in the historical experiment with CM4, focusing on the dynamic sea level plus inverse barometer (i.e.,
![]() $ {\eta}^{\mathrm{dyn}}+{\eta}^{\mathrm{ib}} $
) during the period 1970–2014. Results are shown in Figure 5 and significant changes are reported in Table 2. In this period, roughly 43% of the coastal area experiences significant changes in the mean sea level. Among such changes, positive sea level rise is detected mainly along the US east coast, North and East Africa, as well as Europe and Oceania. Negative trends are simulated along coastlines in East Asia, western North America, and almost the whole South American coast. Importantly, GFDL-CM4 does not exhibit changes in the shapes of distributions in the historical period, which agrees with our tide gauge analysis (Table 2).
$ {\eta}^{\mathrm{dyn}}+{\eta}^{\mathrm{ib}} $
) during the period 1970–2014. Results are shown in Figure 5 and significant changes are reported in Table 2. In this period, roughly 43% of the coastal area experiences significant changes in the mean sea level. Among such changes, positive sea level rise is detected mainly along the US east coast, North and East Africa, as well as Europe and Oceania. Negative trends are simulated along coastlines in East Asia, western North America, and almost the whole South American coast. Importantly, GFDL-CM4 does not exhibit changes in the shapes of distributions in the historical period, which agrees with our tide gauge analysis (Table 2).

Figure 5. Projection onto mean, variance, skewness and kurtosis functions for the GFDL-CM4 historical experiment. We consider the dynamic sea level and inverse barometer (i.e.,
![]() $ {\eta}^{dyn}+{\eta}^{ib} $
) contributions in the period 1970–2014. Statistical significance is computed using the FDR test with threshold
$ {\eta}^{dyn}+{\eta}^{ib} $
) contributions in the period 1970–2014. Statistical significance is computed using the FDR test with threshold
![]() $ \phi =0.05 $
, respectively, for the mean, variance, skewness, and kurtosis slopes. The global thermosteric contribution is not included in the analysis. Only statistical significant slopes are reported.
$ \phi =0.05 $
, respectively, for the mean, variance, skewness, and kurtosis slopes. The global thermosteric contribution is not included in the analysis. Only statistical significant slopes are reported.
Table 2. Percentage of significant coefficients for GFDL-CM4 historical and 1pctCO2 experiments.

Note. For the historical experiment, we consider the dynamic sea level and inverse barometer (i.e.,
![]() $ {\eta}^{dyn}+{\eta}^{ib} $
) contributions in the period 1970–2014. For the 1pctCO2 experiment, we show results both for the dynamic sea level and inverse barometer (i.e.,
$ {\eta}^{dyn}+{\eta}^{ib} $
) contributions in the period 1970–2014. For the 1pctCO2 experiment, we show results both for the dynamic sea level and inverse barometer (i.e.,
![]() $ {\eta}^{dyn}+{\eta}^{ib} $
) and dynamic sea level only (i.e.,
$ {\eta}^{dyn}+{\eta}^{ib} $
) and dynamic sea level only (i.e.,
![]() $ {\eta}^{dyn} $
). Statistical significance is computed using the FDR test with threshold
$ {\eta}^{dyn} $
). Statistical significance is computed using the FDR test with threshold
![]() $ \phi =0.05 $
.
$ \phi =0.05 $
.
We next explore changes in statistics in the last 100 years of the 1pctCO2 experiment with results given in Figure 6 and Table 2. To investigate the main physical drivers of distributional shifts, we first analyze the dynamic sea level
![]() $ {\eta}^{\mathrm{dyn}} $
(Figure 6, left column) and then consider the effect of the inverse barometer, that is,
$ {\eta}^{\mathrm{dyn}} $
(Figure 6, left column) and then consider the effect of the inverse barometer, that is,
![]() $ \eta ={\eta}^{\mathrm{dyn}}+{\eta}^{\mathrm{ib}} $
(Figure 6, right column). We observe that in both cases a large number of coastal locations experience a significant change in the mean of the distribution (Figure 6a,b). The fraction of significant changes is slightly lower when the inverse barometer effect is included (
$ \eta ={\eta}^{\mathrm{dyn}}+{\eta}^{\mathrm{ib}} $
(Figure 6, right column). We observe that in both cases a large number of coastal locations experience a significant change in the mean of the distribution (Figure 6a,b). The fraction of significant changes is slightly lower when the inverse barometer effect is included (
![]() $ \sim 67\% $
vs
$ \sim 67\% $
vs
![]() $ \sim \hskip-1pt 79\% $
) but still much larger than the 43% found in the historical experiment. One difference with the historical experiment is the emergence of mean sea level changes in the South and South-East part of Africa, Indonesia, and India. Additionally, many negative trends in mean sea level found in the historical experiment switch sign, especially in the North-West America, East Asia (i.e., Sea of Japan, East and South China sea) and East Africa.
$ \sim \hskip-1pt 79\% $
) but still much larger than the 43% found in the historical experiment. One difference with the historical experiment is the emergence of mean sea level changes in the South and South-East part of Africa, Indonesia, and India. Additionally, many negative trends in mean sea level found in the historical experiment switch sign, especially in the North-West America, East Asia (i.e., Sea of Japan, East and South China sea) and East Africa.

Figure 6. Projection onto mean, variance, skewness, and kurtosis functions for the GFDL-CM4 experiment with 1%
![]() $ {\mathrm{CO}}_2 $
yearly increase for 100 years. (a,c,e,g) Dynamic sea level only (i.e.,
$ {\mathrm{CO}}_2 $
yearly increase for 100 years. (a,c,e,g) Dynamic sea level only (i.e.,
![]() $ {\eta}^{dyn} $
). (b,d,f,h) Dynamic sea level and inverse barometer contributions (i.e.,
$ {\eta}^{dyn} $
). (b,d,f,h) Dynamic sea level and inverse barometer contributions (i.e.,
![]() $ {\eta}^{dyn}+{\eta}^{ib} $
). Statistical significance is computed using the FDR test with threshold
$ {\eta}^{dyn}+{\eta}^{ib} $
). Statistical significance is computed using the FDR test with threshold
![]() $ \phi =0.05 $
respectively for the mean, variance, skewness, and kurtosis slopes. The global thermosteric contribution is not included in the analysis. Only statistical significant slopes are reported.
$ \phi =0.05 $
respectively for the mean, variance, skewness, and kurtosis slopes. The global thermosteric contribution is not included in the analysis. Only statistical significant slopes are reported.
A major difference with both the observational dataset (Section 4.1) and the CM4 historical experiment is the emergence of changes in higher order moments in the 1pctCO2 experiment. This emergence shows that changes in shapes of daily sea level distributions are indeed possible, at least in simulations as
![]() $ {\mathrm{CO}}_2 $
increases. We detect coherent positive significant changes in variance along the Japan coast (Figure 6c,d). In addition, when also the inverse barometer is included, we see the emergence of positive changes in variance in part of Indonesia and in North- and South-East Africa and East India (Figure 6d). Adding the inverse barometer component always implies a larger fraction of significant changes in second, third, and fourth moments. This result holds for shifts in variance and it is much more evident in the case of third and fourth moments as shown in Table 2. Spatially coherent changes in skewness include positive trends around North Indonesia and in the Philippines and Northern Europe (Figure 6f). Interestingly, we also detect many significant negative changes in skewness, mainly in Japan coasts, North East US, virtually all coasts in the Mediterranean Sea and North East Africa (Figure 6f).
$ {\mathrm{CO}}_2 $
increases. We detect coherent positive significant changes in variance along the Japan coast (Figure 6c,d). In addition, when also the inverse barometer is included, we see the emergence of positive changes in variance in part of Indonesia and in North- and South-East Africa and East India (Figure 6d). Adding the inverse barometer component always implies a larger fraction of significant changes in second, third, and fourth moments. This result holds for shifts in variance and it is much more evident in the case of third and fourth moments as shown in Table 2. Spatially coherent changes in skewness include positive trends around North Indonesia and in the Philippines and Northern Europe (Figure 6f). Interestingly, we also detect many significant negative changes in skewness, mainly in Japan coasts, North East US, virtually all coasts in the Mediterranean Sea and North East Africa (Figure 6f).
Future work will further address possible causes of such higher order changes. Hereafter, we focus mainly on drivers of shifts in kurtosis and on large, spatially coherent changes in the Mediterranean sea and in Northern Europe.
Shifts in the kurtosis functions are negligible in the dynamic sea level contributions and detected only when the inverse barometer is included (Table 2). The largest, spatially coherent domain with changes in kurtosis is found in the Mediterranean, as shown in Figure 6h. This area is marked by significant (negative) changes in both skewness and kurtosis functions. To further explore such distributional shifts, we considered the time series with largest changes in kurtosis in the Mediterranean and analyzed it separately. Results are shown in Appendix G. The histograms for the first and last 40 years of data (see Figure G1c,d) show a decrease in skewness from
![]() $ -0.06 $
to
$ -0.06 $
to
![]() $ -0.37 $
and an excess kurtosis from 0.83 to 0.03 (closer to the Gaussian case of 0).
$ -0.37 $
and an excess kurtosis from 0.83 to 0.03 (closer to the Gaussian case of 0).
Such changes in skewness and kurtosis in the Mediterranean come solely from changes in SLP anomalies (see Figure 6g,h). This result indicates a drop in frequency of (large) negative SLP anomalies (see Eq. 1) and points to a large decrease in frequency of hurricanes in the Mediterranean, the so-called “medicanes,” as recently suggested in González-Alemán et al. (Reference González-Alemán, Pascale, Gutierrez-Fernandez, Murakami, Gaertner and Vecchi2019). We note that while the frequency of medicanes is projected to decrease, the strongest medicanes are expected to intensify (González-Alemán et al., Reference González-Alemán, Pascale, Gutierrez-Fernandez, Murakami, Gaertner and Vecchi2019).
Changes in kurtosis are present in regions outside the Mediterranean sea. The majority of such changes are (a) found to be negative and (b) coming only from the inverse barometer effect (Figure 6h). This possibly points out to changes in the statistics of intense convective systems. This seems to be large in agreement with Priestley and Catto (Reference Priestley and Catto2022) where the authors quantified a robust decrease in cyclone numbers, independent of the season, in CMIP6 models projections. On the other hand, the strongest cyclones are projected to have higher intensities (mean SLP and vorticity) and larger tropospheric wind speed (with changes dependent on different seasons and hemispheres) (Priestley and Catto, Reference Priestley and Catto2022).
A large number of coastal location experience positive changes in skewness in Northern Europe (North sea and Baltic sea). Such changes are already present in the dynamic sea level field,
![]() $ {\eta}^{\mathrm{dyn}} $
, and show no qualitative changes when the inverse barometer is included. Positive changes in skewness in the dynamic sea level field possibly indicate a shift to larger frequency of storm surges. This is in agreement with Gaslikova et al. (Reference Gaslikova, Grabemann and Groll2013), where the authors studied changes in North sea storm surges in future climate scenarios (i.e., 1961–2100 period) by comparing changes in the 99th percentiles of water levels in 30-year windows. Gaslikova et al. (Reference Gaslikova, Grabemann and Groll2013) used a hydrodynamical model and quantified a (small) increase in frequency of such extreme events, consistent with an increase in frequency of intense westerly winds. An increase in frequency of positive large sea level rise anomalies (positive slopes in skewness) in that region is then consistent with such increase in wind forcing. Importantly, such anthropogenic signals are superimposed on large, decadal oscillations leading to uncertainties coming from the system’s internal variability.
$ {\eta}^{\mathrm{dyn}} $
, and show no qualitative changes when the inverse barometer is included. Positive changes in skewness in the dynamic sea level field possibly indicate a shift to larger frequency of storm surges. This is in agreement with Gaslikova et al. (Reference Gaslikova, Grabemann and Groll2013), where the authors studied changes in North sea storm surges in future climate scenarios (i.e., 1961–2100 period) by comparing changes in the 99th percentiles of water levels in 30-year windows. Gaslikova et al. (Reference Gaslikova, Grabemann and Groll2013) used a hydrodynamical model and quantified a (small) increase in frequency of such extreme events, consistent with an increase in frequency of intense westerly winds. An increase in frequency of positive large sea level rise anomalies (positive slopes in skewness) in that region is then consistent with such increase in wind forcing. Importantly, such anthropogenic signals are superimposed on large, decadal oscillations leading to uncertainties coming from the system’s internal variability.
Spatially coherent changes in extreme sea levels over the Mediterranean sea and Northern Europe can be in part linked to projected changes in atmospheric storm track activity and cyclone intensities over Europe as shown by Pinto et al. (Reference Pinto, Ulbrich, Leckebusch, Spangehl, Reyers and Zacharis2007). The authors analyzed ensembles of climate change projections and identified particularly strong reductions of cyclone intensities in subtropical areas such as in the Mediterranean sea and a large increase in extreme surface winds in Great Britain, North, and Baltic seas. Importantly, the role of internal variability was shown to be important and large differences were identified among ensemble members (Pinto et al., Reference Pinto, Ulbrich, Leckebusch, Spangehl, Reyers and Zacharis2007). Such changes were found to mostly hold in the new generation of climate models, and Priestley and Catto (Reference Priestley and Catto2022) quantified a decrease in cyclone activity over the Mediterranean in CMIP6 future projections, together with changes in the North Atlantic storm track.
5. Conclusions
An in-depth assessment of changes in shapes of sea level distributions in observations and in climate simulations has not been addressed in the current literature. In fact, a large focus in the last Intergovernmental Panel on Climate Change report has been on changes in the mean of the distributions (Fox-Kemper et al., Reference Fox-Kemper, Hewitt, Xiao, Adalgeirsdottir, Drijfhout, Edwards, Golledge, Hemer, Kopp, Krinner, Mix, Notz, Nowicki, Nurhati, Ruiz, Sallee, Slangen, Yu, Masson-Delmotte, Zhai, Pirani, Connors, Pean, Berger, Caud, Chen, Goldfarb, Gomis, Huang, Leitzell, Lonnoy, Matthews, Maycock, Waterfield, Yelekci, Yu and Zhou2021). Furthermore, changes in sea level extremes through EVT are often quantified solely as a function of changes in the distributional mean (Tebaldi et al., Reference Tebaldi, Ranasinghe and Vousdoukas2021). This motivated us to address the following questions regarding changes in sea level probability distributions:
-
• Are changes in higher order moments in observations (a) significant but small compared to the shift in the mean or (b) consistent with the climate system’s internal variability?
-
• How do shapes of sea level distribution evolve under
 $ {\mathrm{CO}}_2 $
forcing at centennial time scales, at least in a climate model framework? Which sea level component (i.e., sterodynamic and inverse barometer effects) is responsible for such changes?
$ {\mathrm{CO}}_2 $
forcing at centennial time scales, at least in a climate model framework? Which sea level component (i.e., sterodynamic and inverse barometer effects) is responsible for such changes?
Our work addressed and answered these questions from a novel statistical point of view by exploring changes in sea level distributions in tide gauges and in the GFDL-CM4 model.
To achieve these goals, we introduced a novel and general statistical framework to study changes in both quantiles and moments of a distribution and quantify their significance under the system’s internal variability. Importantly, shifts in moments are captured by suitable orthogonal functions, therefore capturing independent sources of distributional changes. The framework is inspired by the methodology proposed in McKinnon et al. (Reference McKinnon, Rhines, Tingley and Huybers2016) but differs in terms of polynomials and statistical tests. Here, the choice of polynomials follows from the rigorous theoretical work of Cornish and Fisher (Reference Cornish and Fisher1937) and Fisher and Cornish (Reference Fisher and Cornish1960). Their theory allows us to derive a precise formalism to investigate changes in both quantiles and moments. Additionally, the recent work of Chernozhukov et al. (Reference Chernozhukov, Fernàndez-Val and Melly2022) allows for very fast computation of quantile regression, thus making the methodology feasible even when dealing with thousands of time series each with tens of thousands of time steps, as commonly found with climate model applications. In the case of a drifting Gaussian distribution, the first and second polynomials quantify the exact link between changes in moments and quantiles. The third and fourth polynomials adjust for non-Gaussian behavior. Future work may consider the Cornish–Fisher expansion for asymptotic estimates of very large quantiles otherwise difficult (or impossible) to do from data alone, therefore providing a useful alternative to EVT.
The statistical significance test adopts the FDR proposed by Benjamini and Hochberg (Reference Benjamini and Hochberg1995), therefore controlling against multiple testing. The bootstrapping methodology is robust under the sample size
![]() $ B=1000 $
. In general, even for sample sizes as small as
$ B=1000 $
. In general, even for sample sizes as small as
![]() $ B=100 $
we can still obtain meaningful results, as shown for one time series in Figure F2. However, as in any other resampling test, a larger number of samples (i.e.,
$ B=100 $
we can still obtain meaningful results, as shown for one time series in Figure F2. However, as in any other resampling test, a larger number of samples (i.e.,
![]() $ B=5000 $
) would probably be preferred and here avoided because of long run time (same as in McKinnon et al., Reference McKinnon, Rhines, Tingley and Huybers2016). The methodology is linear but still relevant in the case of weak nonlinearities, with an example shown for the Beta distribution in Section 3.4. Strongly nonlinear trends in the mean of the distribution will not be detected by this linear framework, but such nonlinearities would result in significant changes in higher order moments. The underlying physical mechanisms leading to changes in sea level distributions can be nonlinear, such as for a weakening Atlantic meridional overturning circulation (AMOC) commonly found in climate model projections (Weijer et al., Reference Weijer, Cheng, Garuba, Hu and Nadiga2020). For example, in the GFDL-CM4 climate model simulation considered here, the AMOC strength weakened by roughly a factor of two after 100 years of enhanced CO2 forcing (see Figure 13b of Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020). Even so, statistical properties of the sea level distribution retained a close to linear behavior, thus allowing for the methodology developed in this paper to remain useful.
$ B=5000 $
) would probably be preferred and here avoided because of long run time (same as in McKinnon et al., Reference McKinnon, Rhines, Tingley and Huybers2016). The methodology is linear but still relevant in the case of weak nonlinearities, with an example shown for the Beta distribution in Section 3.4. Strongly nonlinear trends in the mean of the distribution will not be detected by this linear framework, but such nonlinearities would result in significant changes in higher order moments. The underlying physical mechanisms leading to changes in sea level distributions can be nonlinear, such as for a weakening Atlantic meridional overturning circulation (AMOC) commonly found in climate model projections (Weijer et al., Reference Weijer, Cheng, Garuba, Hu and Nadiga2020). For example, in the GFDL-CM4 climate model simulation considered here, the AMOC strength weakened by roughly a factor of two after 100 years of enhanced CO2 forcing (see Figure 13b of Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020). Even so, statistical properties of the sea level distribution retained a close to linear behavior, thus allowing for the methodology developed in this paper to remain useful.
We applied the above statistical framework to coastal daily sea level measured by tide gauges. Nearly every record shows a significant change in the mean of the distribution for the period 1970–2017. In contrast, we detect no significant change in higher order moments for the same period, with this conclusion robust to sampling only tide gauges with more than 80 years of data. We conclude that changes in coastal sea level in the historical period exhibited just a shift in the mean, with no significant change in the shape of the probability distribution. Likewise, no changes in higher order statistical moments are found in the GFDL-CM4 historical simulation. Hence, changes in the simulated coastal sea level arise mainly by changes in the mean, which agrees with the tide gauges. We note that multidecadal oscillations could in principle impact statistical attribution in some locations when focusing on “short” datasets. However, the same conclusions are obtained for tide gauges with 47 years (period 1970–2017) and more than 80 years of data. Conclusions on observations are therefore robust on the chosen period.
We then considered a CM4 experiment with 1%/year
![]() $ {\mathrm{CO}}_2 $
forcing, thus allowing us to quantify changes in sea level in a warming (modeled) world. In this experiment, we find (a) a large increase in significant changes in the mean of the distribution compared to the historical run and (b) the emergence of changes in higher order moments.
$ {\mathrm{CO}}_2 $
forcing, thus allowing us to quantify changes in sea level in a warming (modeled) world. In this experiment, we find (a) a large increase in significant changes in the mean of the distribution compared to the historical run and (b) the emergence of changes in higher order moments.
Interestingly, changes in the second and third moments are already present in the dynamic-sea-level-only analysis. These changes are therefore driven solely by the evolution of ocean circulation, caused by changes in water column mass and local steric effects. Such changes get amplified when SLP fluctuations are included, accounting for the inverse barometer effect (Ponte, Reference Ponte2006). Shifts in kurtosis are for the most part negative and possibly consistent with results of Priestley and Catto (Reference Priestley and Catto2022) where the authors observed robust decrease in cyclone numbers, independent of the season, in CMIP6 models projections. One striking difference with the dynamic-sea-level-only analysis is the emergence of large changes in skewness and kurtosis along the Mediterranean coast, possibly pointing to drops in the frequency of medicanes, as shown in González-Alemán et al. (Reference González-Alemán, Pascale, Gutierrez-Fernandez, Murakami, Gaertner and Vecchi2019). A decrease in frequency of medicanes has been shown to hold on average for different regional models, but some model runs show no significant changes (Romera et al., Reference Romera, Gaertner, Sánchez, Domínguez, González-Alemán and Miglietta2017). Larger ensembles and different scenarios are then needed to better quantify the impact of statistical changes in medicanes on coastal sea level. Finally, a large increase in skewness values in the North and Baltic seas is present in the dynamic-sea-level-only analysis and shows no (qualitative) differences with the inclusion of inverse barometer. This is consistent with an increase in frequency of intense westerly winds in that region as shown by Pinto et al. (Reference Pinto, Ulbrich, Leckebusch, Spangehl, Reyers and Zacharis2007) and Gaslikova et al. (Reference Gaslikova, Grabemann and Groll2013).
We note that the GFDL-CM4 does not simulate category 4 and 5 tropical cyclones (see Yin et al., Reference Yin, Griffies, Winton, Zhao and Zanna2020). Hence, shifts in higher order moments of the distributions are likely underestimated in the simulation. Such changes in cyclones frequency should be further explored using different models and scenarios. Furthermore, such information should be taken into account in the context of extreme value attribution where extreme sea level is often modeled solely as a function of the distributional mean.
A limitation of this work is that we focused only on one climate model and we did not consider ensembles of simulations. First, the climate is a chaotic system and ensemble simulations are often needed to explore the system’s variability. Second, climate models are affected by structural model errors and a collection of models is required for more confident climate projections (Smith, Reference Smith2002; Frigg et al., Reference Frigg, Bradley, Du and Smith2014). The emergence of significant changes in higher order moments in the model analyzed here should be seen as a proof of concept rather than a quantitative prediction about the real world. However, this result clearly suggests that quantifying sea level changes solely as a function of the mean of the distribution can be too simplistic. Future work should focus on different models, ensemble runs, and scenarios in order to quantify possible uncertainties coming from different model structures and internal variability.
Results of this study could guide new analyses focused on regions experiencing changes in higher order moments. An example would be to make use of higher resolution regional models to further study dynamical processes in those locations. Additionally, future studies could focus on changes in high (i.e., 0.95) and small (i.e., 0.05) quantiles only in such locations across different models and scenarios. Finally, future work will explore changes in the probability distribution of relevant climate variables other than sea level, from temperature to precipitation, therefore contributing to a better understanding of climate variability and its linkages with natural and anthropogenic forcing.
Acknowledgments
F.F. acknowledges discussions on the topic with Elizabeth Yankovsky, Aaron Match, Simone Contu, and Ryan Shìjié Dù. F.F. acknowledges a correspondence with Blaise Melly with helpful suggestions on fast algorithms for the quantile regression step. We also thank John Krasting and Jan-Erik Tesdal for useful comments on an early draft. Additionally, this work was supported through the NYU IT High Performance Computing resources, services, and staff expertise.
Author contribution
Analysis and investigation: F.F.; Conceptualization: F.F., A.B., and L.Z.; Data curation: F.F., A.B., S.G., and J.Y.; Data visualization: F.F.; GFDL-CM4 model: S.G., J.Y., and M.Z.; Methodology: F.F. and A.B.; Preprocessing of tide gauges: A.B.; Supervision: L.Z. and S.G.; Writing original draft: F.F.; Writing—reviewing and editing: F.F., S.G., L.Z., A.B., J.Y., and M.Z. All authors approved the final submitted draft.
Competing interest
The authors declare none.
Data availability statement
Data are available upon request to fabri.falasca@nyu.edu. Codes and materials are available at https://zenodo.org/badge/latestdoi/623102086.
Ethics statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
The work was supported through NOAA grant NOAA-OAR-CPO-2019-2005530 and by the VoLo foundation. This research was supported by Schmidt Futures, a philanthropic initiative founded by Eric and Wendy Schmidt, as part of its Virtual Earth System Research Institute (VESRI).
Appendix A. Preprocessing tide gauge data
Quality-controlled sea level research-grade tide gauge data were downloaded from the University of Hawaii sea level center (Caldwell et al., Reference Caldwell, Merrifield and Thompson2018) (https://uhslc.soest.hawaii.edu/).
Few locations are associated with multiple distinct tide gauges (indicated by different record IDs). This results in two main issues: (a) different tide gauge records are often measured with respect to different reference levels and (b) some tide gauges have temporally overlapping records. Ideally, such different records should be concatenated into a single time series in a way that remains faithful to the trends observed at each individual station. We address these two issues by implementing the following pipeline for preprocessing the data:
-
• Linear trends from each record are computed.
-
• A residual time series is obtained by detrending each record and concatenating the time series. If any part of two or more records overlap temporally, those portions of the residual time series are averaged.
-
• Slopes for the data are defined at each time by computing the average trend over each record ID. Gaps in the slopes are linearly interpolated. A composite trendline is created by cumulatively integrating the slopes over time.
-
• The residual time series is added to the composite trendline to obtain a composite time series.
Figure A1 illustrates the process for a single tide gauge record at Tarawa, Kiribati.

Figure A1. Illustration of preprocessing of tide gauge for observations at Tarawa, Kiribati. (a) Original time series, with different records demarcated by different colors. Note the different reference points and overlapping timespans. (b) Residual (detrended) time series obtained by detrending records and concatenating values, averaging observations over different records if necessary. (c) Computed trendline obtained by integrating record-averaged slopes over time. (d) Composite processed time series obtained by adding (b) and (c).
Appendix B. Tide gauges with long records
In Table B1, we show the start and end dates for each one of the long records tide gauges considered. Each one of these records includes more than 80 years of data and has less than 20% missing data.
Table B1. Location, starting and ending date of tide gauges with (a) records longer than 80 years and (b) less than 20% missing data.

Appendix C. Exact and sample moments of a distribution
Consider a probability density function
![]() $ P(x) $
, with
$ P(x) $
, with
![]() $ x\,\in\,\mathrm{\mathbb{R}} $
.
$ x\,\in\,\mathrm{\mathbb{R}} $
.
![]() $ P(x) $
satisfies
$ P(x) $
satisfies
![]() $ {\int}_{-\infty}^{\infty }P(x) dx=1 $
. The first moment, that is, the mean, is defined as:
$ {\int}_{-\infty}^{\infty }P(x) dx=1 $
. The first moment, that is, the mean, is defined as:
The central moment
![]() $ {\mu}_n $
of order
$ {\mu}_n $
of order
![]() $ n $
is defined as the
$ n $
is defined as the
![]() $ n $
-th moment about the mean as:
$ n $
-th moment about the mean as:
The variance
![]() $ {\sigma}^2 $
of the distribution is defined as the central moment of order
$ {\sigma}^2 $
of the distribution is defined as the central moment of order
![]() $ n=2 $
, that is,
$ n=2 $
, that is,
![]() $ {\mu}_2 $
:
$ {\mu}_2 $
:
The skewness
![]() $ \gamma $
and excess kurtosis
$ \gamma $
and excess kurtosis
![]() $ \kappa $
of the distribution are defined as the 3rd and 4th standardized central moments:
$ \kappa $
of the distribution are defined as the 3rd and 4th standardized central moments:
Skewness and kurtosis are invariant under translation and rescaling and therefore capture exclusively the shape of the distribution. The focus on excess kurtosis is only a matter of practical convenience as the kurtosis of a normal distribution is equal to 3. In this paper, we are interested in the temporal evolution of the mean (
![]() $ \mu $
), variance (
$ \mu $
), variance (
![]() $ {\sigma}^2 $
), skewness (
$ {\sigma}^2 $
), skewness (
![]() $ \gamma $
), and excess kurtosis (
$ \gamma $
), and excess kurtosis (
![]() $ \kappa $
).
$ \kappa $
).
Note that when focusing on data we can only compute the sample mean, variance, skewness, and kurtosis which serve only as estimators of the exact quantities as defined above. Given a set of
![]() $ N $
observations
$ N $
observations
![]() $ {x}_1,{x}_2,\dots, {x}_N $
, we define the sample mean as:
$ {x}_1,{x}_2,\dots, {x}_N $
, we define the sample mean as:
The sample central moment of order
![]() $ n $
is then defined as
$ n $
is then defined as
Therefore, the sample variance (
![]() $ {\hat{\sigma}}^2 $
), skewness (
$ {\hat{\sigma}}^2 $
), skewness (
![]() $ \hat{\gamma} $
), and excess kurtosis (
$ \hat{\gamma} $
), and excess kurtosis (
![]() $ \hat{\kappa} $
) are defined as:
$ \hat{\kappa} $
) are defined as:
In the main text, we often refer to “moments” without specifying if they are sample or exact moments. The fitting procedure derived in Section 3.2.2 aims in finding changes in the exact statistical moments. The Cornish–Fisher tests shown in Appendices D.1 and D.2 make use of the exact and sample moments, respectively.
Importantly, for simplicity and to ease the derivation in Section 3.2.2, all throughout the paper we refer to the mean, variance, skewness, and kurtosis as
![]() $ \left({m}_1,{m}_2,{m}_3,{m}_4\right) $
.
$ \left({m}_1,{m}_2,{m}_3,{m}_4\right) $
.
Appendix D. Cornish–Fisher expansion
The Cornish–Fisher expansion allows for asymptotic estimations of quantiles of a probability distribution in terms of its first four moments (Cornish and Fisher, Reference Cornish and Fisher1937. We refer the reader to Section 3.2.1 for more details on such formula. Estimations are valid for distributions that do not show large deviations from normality (i.e., reltively small skewness and kurtosis) with Maillard (Reference Maillard2012) showing the domain of validity of such formula. Maillard (Reference Maillard2012), Lamb et al. (Reference Lamb, Monville and Tee2018), and Amédée-Manesme et al. (Reference Amédée-Manesme, Barthélémy and Maillard2019) showed how to correct the skewness and kurtosis parameters in the case of larger deviation from normality. These corrections are not necessary in our study where the polynomials in Section 3.2.2 are defined in the limit of
![]() $ {m}_3 $
and
$ {m}_3 $
and
![]() $ {m}_4 $
approaching zero. In this case,
$ {m}_4 $
approaching zero. In this case,
![]() $ {m}_3 $
and
$ {m}_3 $
and
![]() $ {m}_4 $
are exactly the skewness and kurtosis of the distribution.
$ {m}_4 $
are exactly the skewness and kurtosis of the distribution.
Additionally, here we present two tests using the original expression shown in Section 3.2.1. In the first test, we show how the Cornish–Fisher expansion allows for a trustworthy approximation of the quantile function of a Beta distribution. In a second step, we extend the analysis for sea level stationary time series and show remarkable agreement with the estimated quantiles as computed using the NumPy quantile function (Harris et al., Reference Harris2020). Future work may focus on quantile estimations using the corrected versions such as in Maillard (Reference Maillard2012), Lamb et al. (Reference Lamb, Monville and Tee2018), Amédée-Manesme et al. (Reference Amédée-Manesme, Barthélémy and Maillard2019) to account for large deviations from normality (even if this may not often be necessary for climate observables). Importantly, we note that for large values of skewness and kurtosis we expect large errors for very small and very large quantiles (e.g.,
![]() $ {q}_p $
with
$ {q}_p $
with
![]() $ p=0.0001 $
or
$ p=0.0001 $
or
![]() $ p=1-0.0001 $
) but relatively smaller errors for less extreme values, such as the one considered in this paper (e.g.
$ p=1-0.0001 $
) but relatively smaller errors for less extreme values, such as the one considered in this paper (e.g.
![]() $ {q}_p $
with
$ {q}_p $
with
![]() $ p\,\in\,\left[\mathrm{0.05,0.95}\right] $
).
$ p\,\in\,\left[\mathrm{0.05,0.95}\right] $
).
D.1. Test on Beta distribution
We consider a Beta distribution (see Section 3.4) with parameters
![]() $ \alpha =2 $
and
$ \alpha =2 $
and
![]() $ \beta =12 $
and show it in Figure Ba. In this case, the exact (not sample) mean (
$ \beta =12 $
and show it in Figure Ba. In this case, the exact (not sample) mean (
![]() $ {m}_1 $
), variance (
$ {m}_1 $
), variance (
![]() $ {m}_2 $
), skewness (
$ {m}_2 $
), skewness (
![]() $ {m}_3 $
), and excess kurtosis (
$ {m}_3 $
), and excess kurtosis (
![]() $ {m}_4 $
) take the values
$ {m}_4 $
) take the values
![]() $ \left({m}_1,{m}_2,{m}_3,{m}_4\right)=\left(\mathrm{0.143,0.008,0.988,1.026}\right) $
.The probability distribution is defined for
$ \left({m}_1,{m}_2,{m}_3,{m}_4\right)=\left(\mathrm{0.143,0.008,0.988,1.026}\right) $
.The probability distribution is defined for
![]() $ x\,\in\,\left[0,1\right] $
.
$ x\,\in\,\left[0,1\right] $
.
Given this Beta distribution, we aim in computing quantiles
![]() $ {q}_p $
with
$ {q}_p $
with
![]() $ p\,\in\,\left[\mathrm{0.01,0.99}\right] $
every
$ p\,\in\,\left[\mathrm{0.01,0.99}\right] $
every
![]() $ dp=0.01 $
in three different ways.
$ dp=0.01 $
in three different ways.
-
• We compute the exact quantiles of the Beta distribution with
 $ \alpha =2 $
and
$ \alpha =2 $
and
 $ \beta =12 $
, see blue curve in Figure D1b.
$ \beta =12 $
, see blue curve in Figure D1b. -
• We estimate quantiles under the (wrong) assumption of Gaussianity (green curve in Figure D1b). In this case, every quantile can be estimated by the mean and variance of the distribution.
-
• We correct the previous assumption of normality through the Cornish–Fisher expansion. This allows for asymptotic estimations of the quantiles of the distributions as function of the first four moments. Differences from the ground truth estimation are very small (orange curve in Figure D1b).

Figure D1. A test for the Cornish–Fisher expansion in the case of a Beta distribution. (a) Probability density function of a beta distribution with
![]() $ \alpha =2 $
and
$ \alpha =2 $
and
![]() $ \beta =12 $
. Formulas defining a Beta distributions are shown in Section 3.4. The mean (
$ \beta =12 $
. Formulas defining a Beta distributions are shown in Section 3.4. The mean (
![]() $ {m}_1 $
), variance (
$ {m}_1 $
), variance (
![]() $ {m}_2 $
), skewness (
$ {m}_2 $
), skewness (
![]() $ {m}_3 $
), and excess kurtosis (
$ {m}_3 $
), and excess kurtosis (
![]() $ {m}_4 $
) are also reported. (b) Estimation of quantiles
$ {m}_4 $
) are also reported. (b) Estimation of quantiles
![]() $ {q}_p $
with
$ {q}_p $
with
![]() $ p\,\in\,\left[\mathrm{0.01,0.99}\right] $
every
$ p\,\in\,\left[\mathrm{0.01,0.99}\right] $
every
![]() $ dp=0.01 $
. In blue, we show the ground truth which can be computed analytically for the Beta distribution. In green, we show the estimation obtained under a Gaussian assumption; in this case, the mean
$ dp=0.01 $
. In blue, we show the ground truth which can be computed analytically for the Beta distribution. In green, we show the estimation obtained under a Gaussian assumption; in this case, the mean
![]() $ {m}_1 $
and variance
$ {m}_1 $
and variance
![]() $ {m}_2 $
are enough to compute any quantile. In orange, we show the Cornish–Fisher estimation allowing to correct for nonnormality by computing quantiles as a function of the first four moments.
$ {m}_2 $
are enough to compute any quantile. In orange, we show the Cornish–Fisher estimation allowing to correct for nonnormality by computing quantiles as a function of the first four moments.
D.2. A sea level test
The Cornish–Fisher expansion allows for the computation of any quantile of general distributions as deviations from the corresponding quantile of a normal distribution (Cornish and Fisher, Reference Cornish and Fisher1937; Fisher and Cornish, Reference Fisher and Cornish1960). As far as we know, this approximation has not been used in climate studies. Here, we explore its relevance for sea level studies.
We consider the last 300 years of a 650 years long piControl experiment simulated with the GFDL-CM4 model. The model’s specifics are described in Section 2. The piControl experiment is forced by constant
![]() $ {\mathrm{CO}}_2 $
forcing, set at preindustrial level. Hence, time series at each grid point are close to stationary, with climate model drift relatively small for the 300 years analyzed here. In order to limit the amount of computations in this section, we remapped the ocean model grid to a uniform 1° grid and only points in the latitudinal range
$ {\mathrm{CO}}_2 $
forcing, set at preindustrial level. Hence, time series at each grid point are close to stationary, with climate model drift relatively small for the 300 years analyzed here. In order to limit the amount of computations in this section, we remapped the ocean model grid to a uniform 1° grid and only points in the latitudinal range
![]() $ \left[-60{}^{\circ},60{}^{\circ}\right] $
are considered. Furthermore, we consider 3-day averages, therefore accounting for 36,500 time steps at each grid point. The variable of interest is the dynamic sea level (i.e., “zos”, see Section 1), hereafter referred to as
$ \left[-60{}^{\circ},60{}^{\circ}\right] $
are considered. Furthermore, we consider 3-day averages, therefore accounting for 36,500 time steps at each grid point. The variable of interest is the dynamic sea level (i.e., “zos”, see Section 1), hereafter referred to as
![]() $ {\eta}^{\mathrm{dyn}} $
for consistency with the main discussion in Section 4.
$ {\eta}^{\mathrm{dyn}} $
for consistency with the main discussion in Section 4.
For a sea level time series
![]() $ {\eta}^{\mathrm{dyn}}\left(x,y,t\right) $
at longitude and latitude
$ {\eta}^{\mathrm{dyn}}\left(x,y,t\right) $
at longitude and latitude
![]() $ \left(x,y\right) $
, we compute the 0.95 quantile,
$ \left(x,y\right) $
, we compute the 0.95 quantile,
![]() $ {q}_{0.95} $
. We do so in three different ways.
$ {q}_{0.95} $
. We do so in three different ways.
-
• We compute
 $ {q}_{0.95} $
using the quantile function in the Python, NumPy package (Harris et al., Reference Harris2020). We refer to this value as “Ground Truth” or “GT” under the assumption that 300 years long (stationary) time series are enough to have a good estimate of the true, underlying distribution.
$ {q}_{0.95} $
using the quantile function in the Python, NumPy package (Harris et al., Reference Harris2020). We refer to this value as “Ground Truth” or “GT” under the assumption that 300 years long (stationary) time series are enough to have a good estimate of the true, underlying distribution. -
• We assume that each time series follows a Gaussian distribution. In this case, the 0.95 quantile of each
 $ {\eta}^{\mathrm{dyn}}\left(x,y,t\right) $
can be computed exactly by knowing its mean
$ {\eta}^{\mathrm{dyn}}\left(x,y,t\right) $
can be computed exactly by knowing its mean
 $ {m}_1 $
and variance
$ {m}_1 $
and variance
 $ {m}_2 $
.
$ {m}_2 $
. -
• We adopt the Cornish–Fisher expansion to extend the previous computation to nonnormal statistics. Therefore, we “correct” the Gaussian estimation by accounting for the third and fourth statistical moments
 $ {m}_3 $
and
$ {m}_3 $
and
 $ {m}_4 $
.
$ {m}_4 $
.
Results are shown in Figure D2. In the case of quantiles estimated through Cornish–Fisher, we always obtain closer values to the “Ground Truth” in respect to the Gaussian estimation. This result is clearly shown in the histograms of differences between the “Ground Truth” and the Gaussian and Cornish–Fisher estimations, respectively, in orange and blue (Figure D2d).

Figure D2. A test for the Cornish–Fisher expansion in the case of dynamic sea level. (a) We estimate the quantile 0.95 (
![]() $ {q}_{0.95} $
) for each sea level time series
$ {q}_{0.95} $
) for each sea level time series
![]() $ {\eta}^{dyn}\left(x,y,t\right) $
with the Python, NumPy quantile function. We refer to this estimation as the “Ground Truth” or “GT”. (b) We estimate
$ {\eta}^{dyn}\left(x,y,t\right) $
with the Python, NumPy quantile function. We refer to this estimation as the “Ground Truth” or “GT”. (b) We estimate
![]() $ {q}_{0.95} $
under the assumption of Gaussian statistics. In this case, the mean
$ {q}_{0.95} $
under the assumption of Gaussian statistics. In this case, the mean
![]() $ {m}_1 $
and variance
$ {m}_1 $
and variance
![]() $ {m}_2 $
of each time series
$ {m}_2 $
of each time series
![]() $ {\eta}^{dyn}\left(x,y,t\right) $
are enough to compute any quantile. (c) We correct the estimation of
$ {\eta}^{dyn}\left(x,y,t\right) $
are enough to compute any quantile. (c) We correct the estimation of
![]() $ {q}_{0.95} $
in panel (b) through the Cornish–Fisher expansion. (d) We consider the histogram of differences between the “Ground Truth” (panel (a)) and the Gaussian and Cornish–Fisher estimations shown in panel (b,c). Note how the differences are greatly reduced using the CF expansion relative to the Gaussian expansion.
$ {q}_{0.95} $
in panel (b) through the Cornish–Fisher expansion. (d) We consider the histogram of differences between the “Ground Truth” (panel (a)) and the Gaussian and Cornish–Fisher estimations shown in panel (b,c). Note how the differences are greatly reduced using the CF expansion relative to the Gaussian expansion.
Appendix E. Tide gauges: p-values and FDR
In this work, p-values are computed from the block-bootstrapped distribution (see Section 3.3). Here, we analyze the robustness of block size when computing p-values and present results in Figure E1. Results are robust in the case of blocks of one season (90 days), 6 months, and 1 year while diverging for smaller sizes such as 30 days. The results shown in the main paper using 1 season are then robust and this choice is adopted throughout the paper.

Figure E1.
p-values for tide gauges data in the 1970–2017 period. (a–d) Sorted p-values for changes in distributional mean, variance, skewness, and kurtosis, respectively. p-values have been computed from the block-bootstrapped distribution. These plots investigate the robustness of the p-value computation under blocks of 30, 90, 180, and 365 days are reported. Convergence is achieved starting from 90 days (block chosen in the analysis). The false discovery rate
![]() $ \phi =0.05 $
is also reported.
$ \phi =0.05 $
is also reported.
Appendix F. Tide gauge data at Balboa, Panama
The only two long-record tide gauges with changes in higher order moments were both found in Panama. In Figure F1, we show one of the two tide gauges for which we identified a statistical significant change in variance.
The full time series is shown in Figure F1a and the quantile slopes together with the projection onto polynomials is shown in Figure F1b. The first and last 40 years of the time series are plotted in Figure F1c,d. Figure F1d clearly shows larger variance in respect to the first 40 years. At least in part, these changes can be explained by large sea level oscillations forced by the El Niño Southern Oscillation (ENSO). Large, positive sea level anomalies can be clearly identified across the years 1982/1983 and 1997/1998 where two large El Niño were recorded (Wang et al., Reference Wang2019). Very large, persistent negative sea level anomalies can be seen across the years 1988/1989 in correspondence of a strong La Niña event.
In Figure F2, we provide a justification for the choice of sample size
![]() $ B $
to infer the bootstrapped distribution. The bootstrapped distribution is then used to estimate the statistical significance in changes in mean, variance, skewness, and kurtosis (see Section 3). Here, we show that even with sample sizes as small as
$ B $
to infer the bootstrapped distribution. The bootstrapped distribution is then used to estimate the statistical significance in changes in mean, variance, skewness, and kurtosis (see Section 3). Here, we show that even with sample sizes as small as
![]() $ B=100 $
we obtain the same results in terms of statistical significance as with
$ B=100 $
we obtain the same results in terms of statistical significance as with
![]() $ B=5000 $
when looking at 95% confidence level. Generally, larger sample sizes are always preferred and in this paper we adopt
$ B=5000 $
when looking at 95% confidence level. Generally, larger sample sizes are always preferred and in this paper we adopt
![]() $ B=1000 $
. Nonetheless, when focusing on many time series it could be useful considering smaller
$ B=1000 $
. Nonetheless, when focusing on many time series it could be useful considering smaller
![]() $ B $
for faster computation.
$ B $
for faster computation.

Figure F1. Analysis of the Balboa, Panama tide gauge from 1907-06-20 to 2018-12-31. (a) Recorded sea level at Balboa, Panama. (b) Linear quantile slopes for the time series shown in panel (a). The slopes
![]() $ {\beta}_1\left({q}_p\right) $
are computed for
$ {\beta}_1\left({q}_p\right) $
are computed for
![]() $ p\in \left[\mathrm{0.05,0.95}\right] $
every
$ p\in \left[\mathrm{0.05,0.95}\right] $
every
![]() $ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c,d) Time series in the first and last 40 years of recorded sea level.
$ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c,d) Time series in the first and last 40 years of recorded sea level.

Figure F2. Analysis of the Balboa, Panama tide gauge from 1907-06-20 to 2018-12-31. Here, we show the bootstrapped distribution to infer statistical significance in changes in the mean, variance, skewness, and kurtosis (number of bins is set to 50). The dashed black lines indicate the slopes in moments. We focus on the dependence of our analysis to the sample size
![]() $ B $
used for to infer the null distribution. Here
$ B $
used for to infer the null distribution. Here
![]() $ B $
ranges from
$ B $
ranges from
![]() $ B=100 $
(first row) to
$ B=100 $
(first row) to
![]() $ B=5000 $
(fourth row). In all examples, the mean and variance show significant changes at the 95% level while changes in skewness and kurtosis are found to be not significant. This means that bootstrapping with sample sizes as low as
$ B=5000 $
(fourth row). In all examples, the mean and variance show significant changes at the 95% level while changes in skewness and kurtosis are found to be not significant. This means that bootstrapping with sample sizes as low as
![]() $ B=100 $
can still give meaningful results. In all our analysis in this paper, we used
$ B=100 $
can still give meaningful results. In all our analysis in this paper, we used
![]() $ B=1000 $
.
$ B=1000 $
.
Appendix G. Time series in the GFDL-CM4 Mediterranean sea
The 1pctCO2 simulation shows many changes in higher order moments. Numerous changes in the third and fourth moments are found in the Mediterranean sea. Here, we extract the time series in the (GFDL-CM4) Mediterranean with largest changes in kurtosis (fourth moment). We then plot the probability distributions in the first and last 40 years of the simulation showing the large changes in shapes of distributions. This result is shown in Figure G1.

Figure G1. (a) Time series showing the largest changes in kurtosis in the Mediterranean sea for the GFDL-CM4 model 1pctCO2 run. (b) Linear quantile slopes for the time series shown in panel (a). The slopes
![]() $ {\beta}_1\left({q}_p\right) $
are computed for
$ {\beta}_1\left({q}_p\right) $
are computed for
![]() $ p\in \left[\mathrm{0.05,0.95}\right] $
every
$ p\in \left[\mathrm{0.05,0.95}\right] $
every
![]() $ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c,d) Histograms for the first and last 40 years of data of the time series shown in panel (a).
$ dp=0.05 $
and indicated as blue dots. The black dashed line indicates the projection onto polynomials as defined in Eq. (7). Green “check” marks indicate statistically significant (95% confidence level) changes in moments; red “crosses” indicate nonsignificant changes. (c,d) Histograms for the first and last 40 years of data of the time series shown in panel (a).