Impact Statement
This paper explores cyclone landfall prediction over the North Indian Ocean by predicting the latitude, longitude, and intensity. With the help of mutual information based feature selection and a deep neural network model trained over phases of a cyclone, this study is helpful in disaster management. The study also emphasizes upon the importance of feature selection, by highlighting some important parameters conducive for the prediction task and its accuracy. The efficacy of the proposed method is further validated by the data of a recent cyclonic storm Fani.
1. Introduction
A tropical cyclone (also referred to as a hurricane or typhoon) is a rotating storm system formed over warm waterbodies in the tropical regions across the globe. After intensification over warm ocean waters, numerous cyclones advance toward coastal land where upon arrival it wreaks massive damage to the economy and lives, before losing its intensity and characteristic structure. US National Hurricane Centre defines cyclone landfall as the “intersection of the surface center of a tropical cyclone with a coastline.” An estimate of 16.75% increase in cyclone intensity over the North Indian Ocean (NIO) has been observed over the past four decades, rendering coastal settlements vulnerable to severe damage (Albert et al., Reference Albert, Krishnan, Bhaskaran and Singh2021). With increasing settlements along the coastline and rising ocean temperature, determining cyclone trajectory and landfall is crucial for disaster response. The task of predicting cyclone trajectory and landfall has evolved over the years from statistical models to hybrid and data-driven approaches to enhance the accuracy of the prediction. But in-situ prediction of a cyclone has always been a difficult task owing to the highly fluctuant behavior of the storms. The trajectory of a storm is not only dependent on the past track data but also on its interaction with several external environmental factors and the local orography of the coastline. Owing to land-sea friction, landfalling cyclones demonstrate rapid asymmetric transition from a highly symmetric structure (Powell, Reference Powell1987; Blackwell, Reference Blackwell2000). Thus the precise prediction of a cyclone track on landfall still remains quite challenging. Several studies on climate-cyclone interactions have used time-delayed correlation and the discovery of causal links in climate-cyclogenesis has been conducted to address this. Although time-delayed correlation analysis has been the most commonly used technique, correlation does not imply causation.
While achieving high prediction accuracy is a goal in cyclone landfall study, knowledge of the environmental factors modulating the intensity and direction is also important. Thus in this study, we intend to address the task by incorporating a feature selection method with mutual information (MI) into the prediction model that not only improves the accuracy but also directs toward possible interaction among the variables ultimately governing the changing parameters of a cyclone system. While numerous feature selection methods have been utilized for multivariate time series analysis for reducing the computational cost of predictive modeling along with an increase in accuracy, namely wrapper and filter methods, the former comes with a computation overhead and filter methods utilize statistical techniques which prove much more efficient. Under reasonable assumptions, MI has proved to increase accuracy for regression tasks (Frénay et al., Reference Frénay, Doquire and Verleysen2013). We have chosen MI, a filter method for detecting a concise set of features conducive to our forecasting task. While recurrent neural network (RNN) has shown the capability of modeling nonlinear temporal relations of a hurricane, their prediction accuracy can be highly improved by including causally linked predictors specific to the task. Also, using dilated recurrent neural network (DRNN) provides much better performance over conventional recurrent models with exponentially increased dilation, dilated recurrent skip connection, and flexibility of using any recurrent units as the building block. Thus we have used DRNN with gated recurrent unit (GRU) cells for the prediction model. Data from Fani, a recent devastating storm is kept aside while training the model and is used to check the efficacy of the proposed methodology.
2. Previous Works
The problem of cyclone track prediction has been addressed typically by numerical models, statistical models, dynamic models, and hybrid models. But the dynamical, statistical, and numerical models are computationally expensive and demand huge computation power. With the recent increase in computation power of GPUs and TPUs along with more availability in tracking data from cyclones worldwide, the task of cyclone prediction has observed a more data-driven solution. Globenet (Hong et al., Reference Hong, Kim, Joh and Song2017) was designed to take 3D satellite imagery as input and predict the location of a single typhoon center by using complex convolutional neural network (CNN). Artificial neural networks were used to forecast the cyclone track from satellite images (Kovordányi and Roy, Reference Kovordányi and Roy2009). Principal component analysis (PCA) was used for cyclone eye detection (DeMaria et al., Reference DeMaria, Chirokova, Knaff and Dostalek2015). RNN was used to predict hurricane trajectory (Alemany et al., Reference Alemany, Beltran, Perez and Ganzfried2019). A fusion network using past track data and reanalysis data was used to predict the hurricane location (Giffard-Roisin et al., Reference Giffard-Roisin, Yang, Charpiat, Kégl and Monteleoni2018). While forecasting cyclone track and eye detection have been studied, very few (Kumar et al., Reference Kumar, Biswas and Pandey2021) have addressed the issue of predicting the landfall location and intensity of a cyclone, especially for the NIO basin which observes a significant amount of devastating cyclones each year.
Causal interaction among the units in a system is crucial to understand the underlying principles governing it. To this end, numerous studies and methods have been proposed over the years. Wiener proposed the precedence of the cause/driver over the effect/recipient. This idea of incorporating historical data in understanding the causal interaction and direction was later formalized by Clive Granger in the form of Granger Causality, built on the notion that a cause can help predict future effects beyond that which can be predicted purely based on their own previous value. But this found limited usage in systems with high nonlinearity. Thus transfer entropy was proposed that measures the reduction of signal uncertainty through probability distribution, by incorporating the historical values of both the cause and effect. But this process comes with huge computational overhead due to the curse of dimensionality. Thus MI forms a more robust yet lightweight alternative.
3. Background
A major factor in analyzing multivariate time series data is detecting temporal precedence among the features and predict the consequences of possible interaction among units in the system where interventional techniques like perturbation and manipulation seems infeasible. Granger Causality has been used extensively for this purpose, although the presence of nonlinearity renders the analysis questionable (Li et al., Reference Li, Xiao, Zhou and Cai2018). Filter-based alternatives like MI have been quite adept in estimating the relevance of a feature subset in predicting the target variable.
3.1. Mutual information
MI is a feature selection method based on information gain that gives the statistical dependence between two variables, that is the amount of information obtained from one random variable given another. It measures mutual dependence between two random variables and gives the reduction in uncertainity in learning about a variable, given another variable. Its value varies between 0 and 1, with a lower value indicating independence among the concerned variables. Given two random variables ![]() $ X $ and
$ X $ and ![]() $ Y $ with their respective probability density function
$ Y $ with their respective probability density function ![]() $ {f}_x $ and
$ {f}_x $ and ![]() $ {f}_y $ and domains
$ {f}_y $ and domains ![]() $ {D}_X $ and
$ {D}_X $ and ![]() $ {D}_Y $, with the joint probability density function
$ {D}_Y $, with the joint probability density function ![]() $ {f}_{X,Y} $, the MI can be defined as
$ {f}_{X,Y} $, the MI can be defined as
 $$ I\left(X;Y\right)\hskip0.35em =\hskip0.35em -{\int}_{D_X}{\int}_{D_Y}{f}_{X,Y}\left(x,y\right)\log \frac{f_{X,Y}\left(X,Y\right)}{f_X(X){f}_Y(Y)} dxdy. $$
$$ I\left(X;Y\right)\hskip0.35em =\hskip0.35em -{\int}_{D_X}{\int}_{D_Y}{f}_{X,Y}\left(x,y\right)\log \frac{f_{X,Y}\left(X,Y\right)}{f_X(X){f}_Y(Y)} dxdy. $$ This can be represented as ![]() $ I\left(X;Y\right)\hskip0.35em =\hskip0.35em H(Y)-H\left(Y|X\right) $ where
$ I\left(X;Y\right)\hskip0.35em =\hskip0.35em H(Y)-H\left(Y|X\right) $ where ![]() $ H(X)\left(=-{\int}_{D_X}{f}_X(x)\log {f}_X(x) dx\right) $ is the entropy and
$ H(X)\left(=-{\int}_{D_X}{f}_X(x)\log {f}_X(x) dx\right) $ is the entropy and ![]() $ H\left(Y|X\right)\left(=-{\int}_{D_X}{\int}_{D_Y}{f}_{X,Y}\left(x,,,\hskip-0.55em ,y\right)\log \frac{f_X(x)}{f_{X,Y}\left(x,,,\hskip-0.55em ,y\right)} dxdy\right) $ is the conditional entropy for
$ H\left(Y|X\right)\left(=-{\int}_{D_X}{\int}_{D_Y}{f}_{X,Y}\left(x,,,\hskip-0.55em ,y\right)\log \frac{f_X(x)}{f_{X,Y}\left(x,,,\hskip-0.55em ,y\right)} dxdy\right) $ is the conditional entropy for ![]() $ Y $ given
$ Y $ given ![]() $ X $ (Frénay et al., Reference Frénay, Doquire and Verleysen2013). MI has several benefits over other statistical techniques to understand the cooperative nature of a system such as: ability to detect any form of relationship between variables, both linear and nonlinear and also ease in interpreting as the amount of shared information between data sets.
$ X $ (Frénay et al., Reference Frénay, Doquire and Verleysen2013). MI has several benefits over other statistical techniques to understand the cooperative nature of a system such as: ability to detect any form of relationship between variables, both linear and nonlinear and also ease in interpreting as the amount of shared information between data sets.
3.2. Dilated recurrent neural network
While variants of the RNN have been used traditionally for various sequential learning problems, their learning range of temporal dependencies is inhibited by gradient problems and has low computational efficiency. DRNN is a multilayer, cell-independent variant of RNN, powered by dilated recurrent skip connection that overcomes those problems while being computationally efficient and flexible in terms of the types of RNN cells stacked together as building blocks of the neural network (Chang et al., Reference Chang, Zhang, Han, Yu, Guo, Tan, Cui, Witbrock, Hasegawa-Johnson and Huang2017). DRNN allows parallelization as demonstrated in the following figure: (a) demonstrates skip connection in a single layer recurrent neural cell and (b) demonstrates the parallel execution of the same skip connection that reduces the sequence length by four times.

As shown in the figure, the four cells {![]() $ {c}_{4t}^{(l)} $}, {
$ {c}_{4t}^{(l)} $}, {![]() $ {c}_{4t+1}^{(l)} $}, {
$ {c}_{4t+1}^{(l)} $}, {![]() $ {c}_{4t+2}^{(l)} $} and {
$ {c}_{4t+2}^{(l)} $} and {![]() $ {c}_{4t+3}^{(l)} $} for the input subsequence {
$ {c}_{4t+3}^{(l)} $} for the input subsequence {![]() $ {x}_{4t}^{(l)} $}, {
$ {x}_{4t}^{(l)} $}, {![]() $ {x}_{4t+1}^{(l)} $}, {
$ {x}_{4t+1}^{(l)} $}, {![]() $ {x}_{4t+2}^{(l)} $} and {
$ {x}_{4t+2}^{(l)} $} and {![]() $ {x}_{4t+3}^{(l)} $} can be computed in parallel. This greatly improves the computational cost of training when compared to a regular RNN. The dilated skip connection which connects information flow between the layers by skipping certain timesteps can be represented as
$ {x}_{4t+3}^{(l)} $} can be computed in parallel. This greatly improves the computational cost of training when compared to a regular RNN. The dilated skip connection which connects information flow between the layers by skipping certain timesteps can be represented as
where ![]() $ {c}_t^{(l)} $ is the cell at layer
$ {c}_t^{(l)} $ is the cell at layer ![]() $ l $ at time
$ l $ at time ![]() $ t $,
$ t $, ![]() $ {s}^{(l)} $ is the skip length,
$ {s}^{(l)} $ is the skip length, ![]() $ {x}_t^{(l)} $ is the layer
$ {x}_t^{(l)} $ is the layer ![]() $ l $ input at time
$ l $ input at time ![]() $ t $, and
$ t $, and ![]() $ f\left(\right) $ is any RNN operation (like LSTM, GRU, or vanilla RNN). Here the dependency on previous cell state
$ f\left(\right) $ is any RNN operation (like LSTM, GRU, or vanilla RNN). Here the dependency on previous cell state ![]() $ {c}_{t-1}^{(l)} $ similar to that of a regular skip connection is omitted and instead a flexible dependence on a skipped previous cell state is included. This deals away with the conventional gradient problems faced by typical RNNs, extending the range of temporal dependence. In this setting, multiple recurrent layers are stacked that may comprise of vanilla RNN, LSTM or GRU, where the dilations are increased exponentially along the layers. Thus the dilation of the
$ {c}_{t-1}^{(l)} $ similar to that of a regular skip connection is omitted and instead a flexible dependence on a skipped previous cell state is included. This deals away with the conventional gradient problems faced by typical RNNs, extending the range of temporal dependence. In this setting, multiple recurrent layers are stacked that may comprise of vanilla RNN, LSTM or GRU, where the dilations are increased exponentially along the layers. Thus the dilation of the ![]() $ l $th layer
$ l $th layer ![]() $ {s}^{(l)} $ can be represented as
$ {s}^{(l)} $ can be represented as
for ![]() $ l\hskip0.35em =\hskip0.35em 1,\hskip0.35em 2,\hskip0.35em \dots, \hskip0.35em L. $, where
$ l\hskip0.35em =\hskip0.35em 1,\hskip0.35em 2,\hskip0.35em \dots, \hskip0.35em L. $, where ![]() $ {M_0}^l $ is the starting dilation.
$ {M_0}^l $ is the starting dilation.
The efficacy of a DRNN can further be quantified using mean recurrent length (Chang et al., Reference Chang, Zhang, Han, Yu, Guo, Tan, Cui, Witbrock, Hasegawa-Johnson and Huang2017) which is a measure of the average dilation across different time spans within a cycle, if we take the cyclic graph representation of a RNN. In case of DRNN, the Mean Recurrent Length is quite small as compared to a regular skip connection RNN and this implies that the past information travels along fewer edges in case of a DRNN, hence encounters much less attenuation.
4. Data set
Regional Specialized Meteorological Centers across the world are tasked by the World Meteorological Organization to record and provide the tropical cyclone track along with the Best Track Data. This comprises the best location estimates of the storm track throughout the lifetime of a cyclone along with intensity, central pressure, and so forth. For this study, the data set has been obtained from RSMC New Delhi that looks over the storms occurring over NIO, comprising storm tracks from the year 1982 to June 2020. The data comprises essential features of the storm track at each point at three hourly intervals. Along with the original features, distance and direction have been derived from the data set as additional features (Alemany et al., Reference Alemany, Beltran, Perez and Ganzfried2019), crucial for tracking the trajectory behavior of each storm track. A major important factor affecting the trajectory of a cyclone is Sea Surface Temperature, which is appended to the data set (Kumar et al., Reference Kumar, Biswas and Pandey2021). In this study, we address the problem of cyclone landfall and thus only the data till the landfall have been considered. Data of Fani, one of the strongest cyclones occurring over the NIO since 1999 have been kept aside during the training phase to test proposed model.
5. Proposed Methodology
5.1. Feature selection
Usually feature selection methods can be categorized into filter approaches (using only the data for feature selection, like the PCA) and wrapper approaches (using an algorithm for feature selection, like recursive feature elimination [RFE]). Wrapper methods evaluate multiple models with various combinations of the features to find the optimal subset of features most conducive to the task. While this exhaustively searches the feature space, it comes with a huge computation overhead. On the other hand, Filter methods use statistical techniques to evaluate the feature space based on some criterion, which is less computationally expensive. Since Tropical Cyclone Best Track Data contains temporal ordering, it is critical to identify the most important predictors from the data set. In this task, we use MI as the feature selection method to exploit the connection between causation and prediction, in that we use the historical data of a storm to identify the feature subset that gives the maximum information gain while considering our prediction tasks, namely the latitude, longitude, and intensity of a storm at the time of landfall. From the data set, MI discovered for each prediction task is demonstrated in Table 1. Features having ![]() $ \mathrm{MI}>0.18 $ have been selected (values rounded off to three decimal places).
$ \mathrm{MI}>0.18 $ have been selected (values rounded off to three decimal places).
Table 1. Pairwise mutual information between features and predictand.
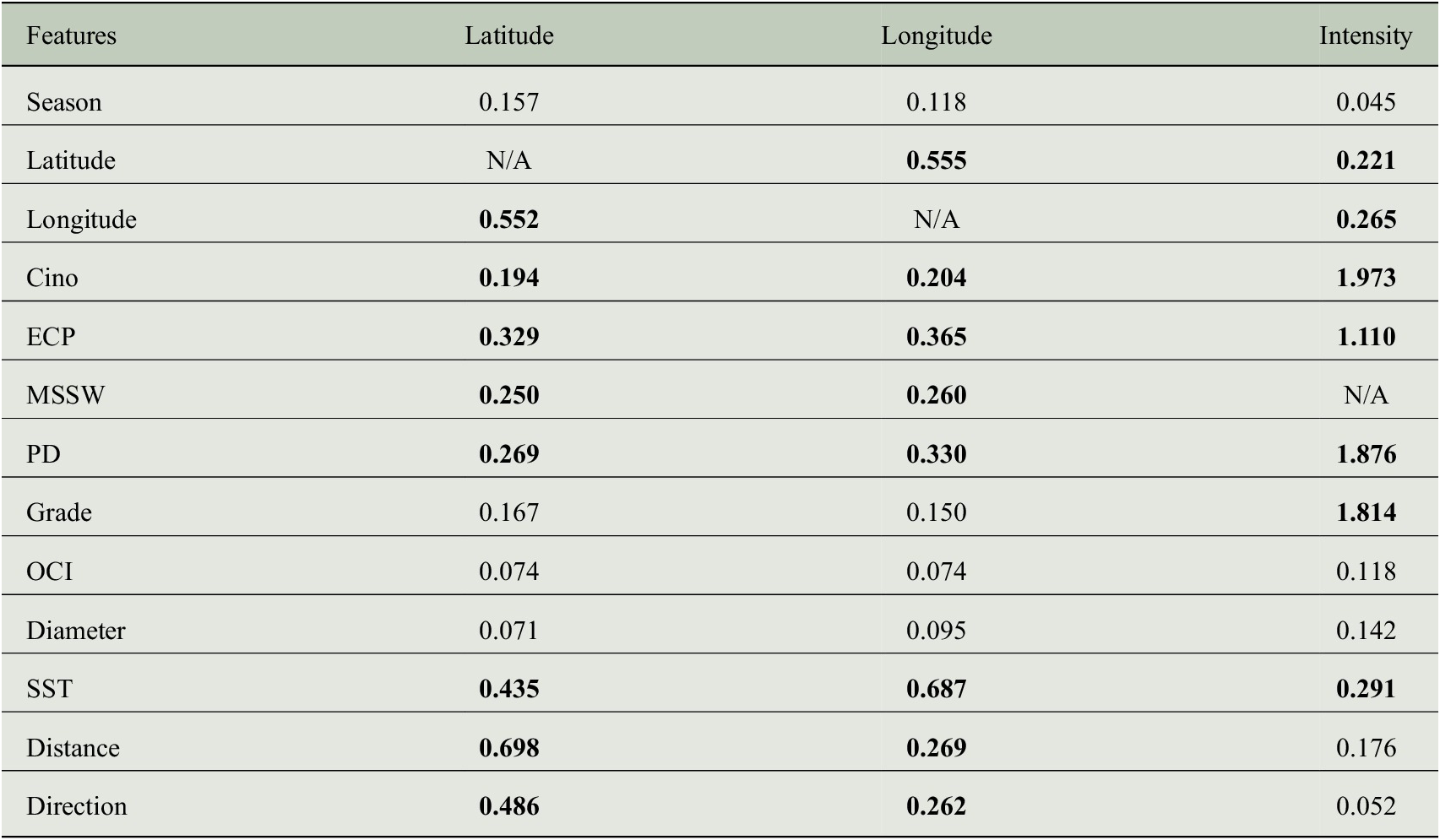
Note: Bold signifies selected features from the set of all features.
Abbreviations: Cino, T. No.; ECP, estimated central pressure; MSSW, maximum sustained surface wind; OCI, outermost closed isobar; PD, pressure drop; SST, sea surface temperature.
5.2. DRNN using GRU block
For the cyclone landfall study, we have dedicated three different networks (with DRNN blocks and fitted with MI) to determine the latitude, longitude, and intensity of a cyclonic storm over NIO for 12, 18, 24, and 36 training hours. We have used a three-layer DRNN network with 512, 256, and 128 GRU cells in each of the layers for determining the latitude and longitude of cyclone landfall. For predicting the intensity, we have used a three-layer DRNN with 2048, 1024, and 512 GRU cells in each of the layers.
5.3. Methodology/steps
Step 1: Cyclone Best Track Data obtained from IMD.
Step 2: Additional features’ distance and direction are calculated and added to the original data set.
Step 3: Filter the data set to keep only the cyclone track data having landfall and eliminate the data from cyclones that originate and dissipate over the ocean.
Step 4: Estimate the MI to select the important features for each of the target variables latitude, longitude, and intensity.
Step 5: A DRNN with GRU cells as building block is assigned for each of the three prediction tasks.
Step 6: Check the efficacy of the proposed method on the test data set and Fani data set.
5.4. Experimental setup
PyTorchFootnote 1 has been used for designing the model. For performing the experiments, the GPU available on Google Colab has been used which allocates one of Nvidia K80, P100, or P4 depending on availability. For the intensity prediction task, the model was run for 400 epochs, with a learning rate of 0.001. For predicting the latitude and longitude, the model was run for 250 epochs, with a learning rate of 0.001. The loss criterion for training the models is MSE loss. For the cyclone intensity prediction task, we have used Adam optimizer and for the prediction of latitude and longitude, Adamax optimizer has been used. The activation function chosen for predicting the intensity of a storm at landfall is Swish (Ramachandran et al., Reference Ramachandran, Zoph and Le2017), a gated variant of sigmoid activation function. For the prediction tasks of Latitude and Longitude, ReLU activation function has been used.
6. Results
We study the Tropical Cyclones over the NIO and investigate vital parameters like the location (latitude and longitude) and intensity of a cyclone, imperative for landfall study of cyclones, disaster management, and mitigation. For predicting each of these tasks, we have extracted different sets of features (from the historical data) that are conducive to the prediction task at hand. We have designed three models with different features as input and have used DRNN (with GRU blocks) for the prediction task. Results from recent work (Kumar et al., Reference Kumar, Biswas and Pandey2021) have been considered for a comparison study, where stacked LSTM (three layers) and Bi-LSTM (three layers) have been used for modeling similar prediction objectives. We report the results of the proposed method for latitude, longitude, and intensity for a time period of 12, 18, 24, and 36 training hours. The fivefold validation accuracy in terms of RMSE and MAE has been reported to demonstrate the efficacy of the proposed technique. Data from the recently occurred cyclone Fani have been kept separately while training the model and the model performance on the landfall prediction of this cyclone is also shown for each of the prediction tasks. While the results of Longitude and Intensity show a clear improvement in prediction accuracy, the proposed method gives a comparable performance for predicting the Latitude.
The model performance in predicting the latitude is demonstrated in Table 2. Similarly, the longitude prediction for cyclone landfall is shown in Table 3. A crucial parameter in landfall study of a cyclone is the prediction of the storm intensity during landfall. The results obtained for predicting the intensity (maximum sustained wind speed) are shown in Table 4.
Table 2. RMSE, MAE results for landfall latitude for different read times.
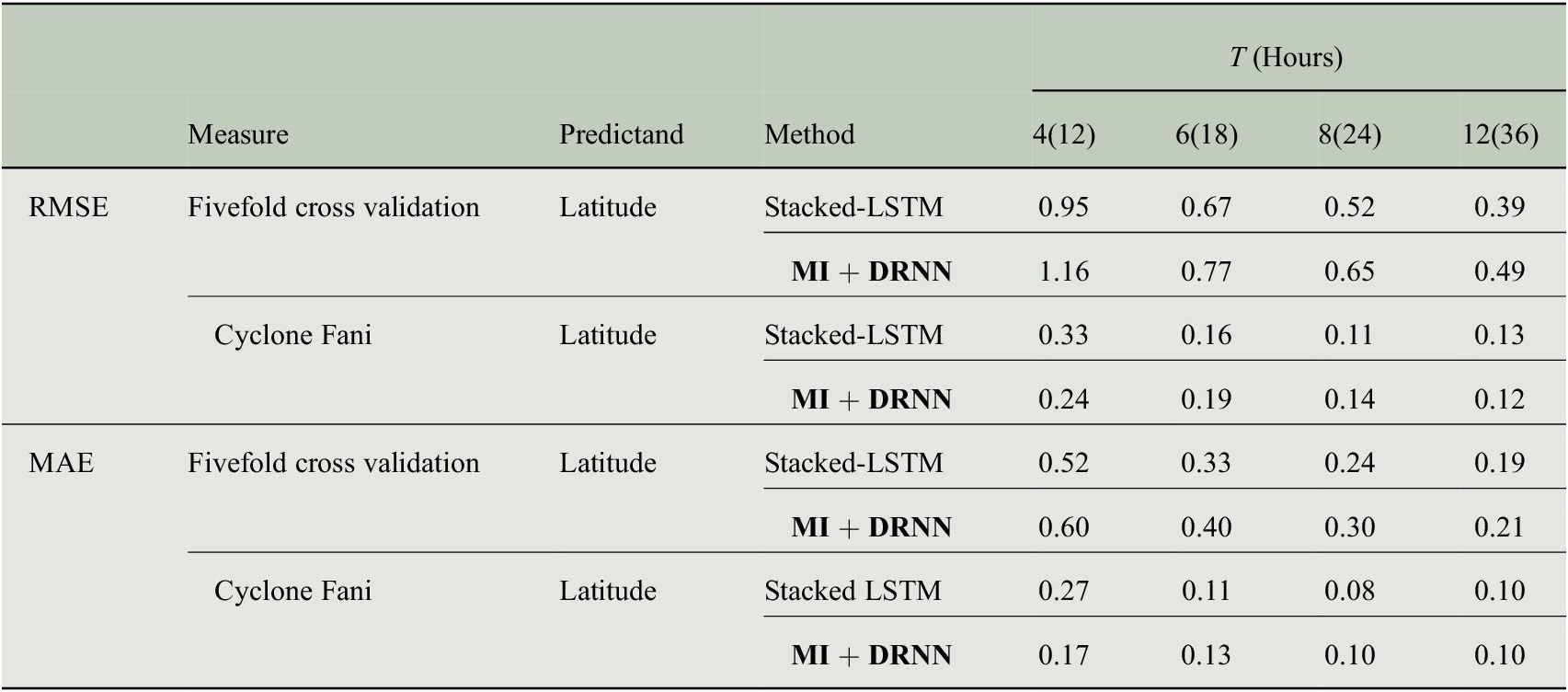
Note: Bold signifies the result of our proposed method.
Table 3. RMSE, MAE results for landfall longitude for different read times.
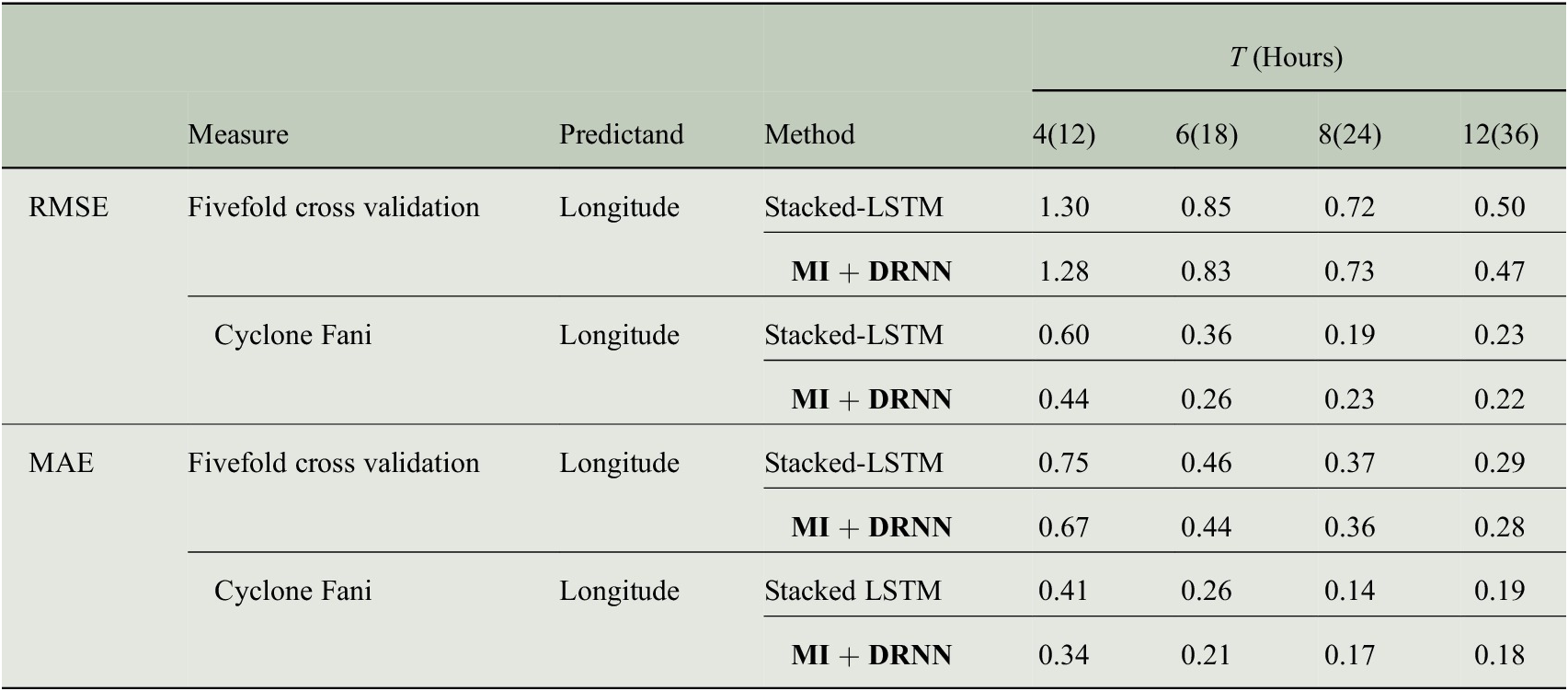
Note: Bold signifies the result of our proposed method.
Table 4. RMSE, MAE results for landfall intensity for different read times.
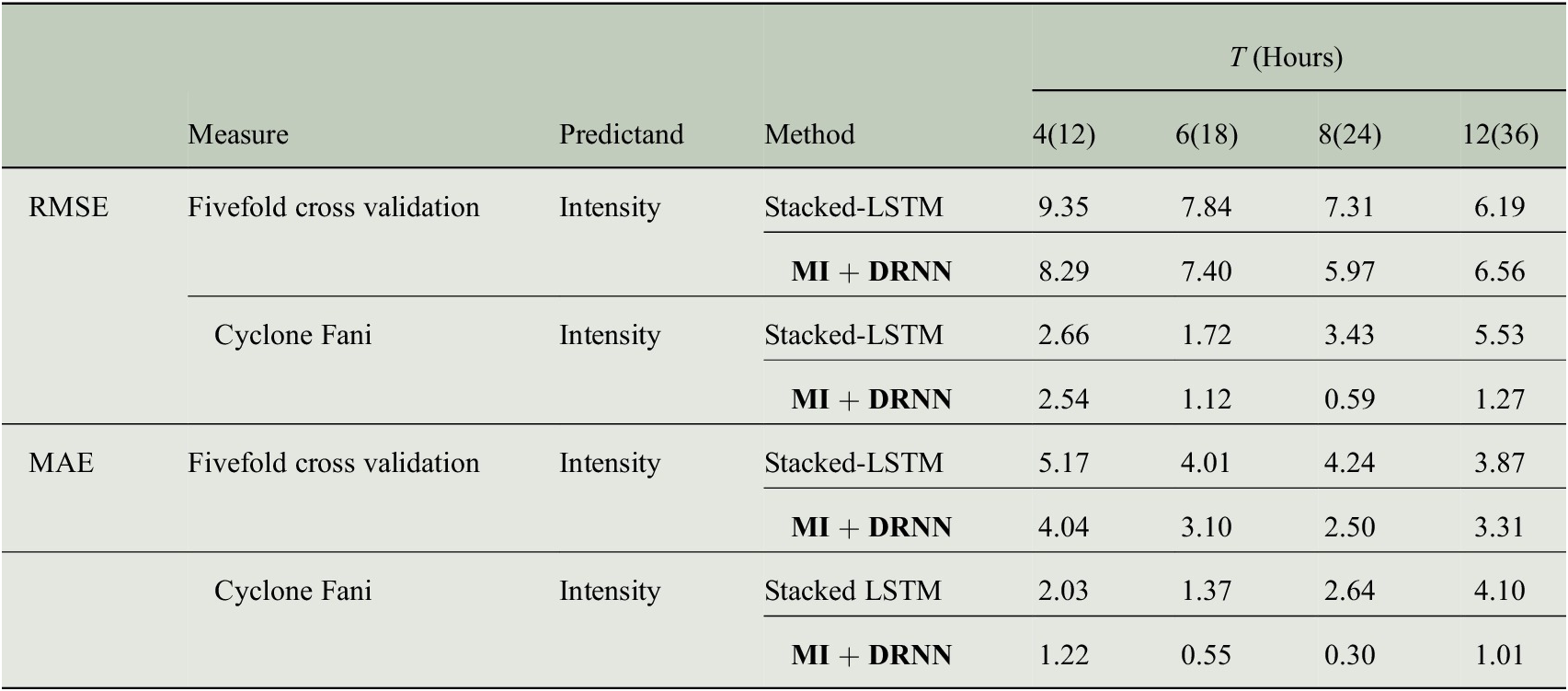
Note: Bold signifies the result of our proposed method.
The discovered factors modulating the trajectory and intensity of a cyclonic storm possess some latent connection while some can be attributed to physical laws, like the pressure drop and intensity are related by Dvorak technique (![]() $ {V}_{\mathrm{max}}=14.2\times \sqrt{\Delta P} $, where
$ {V}_{\mathrm{max}}=14.2\times \sqrt{\Delta P} $, where ![]() $ {V}_{\mathrm{max}} $ is the maximum wind velocity and
$ {V}_{\mathrm{max}} $ is the maximum wind velocity and ![]() $ \Delta P\hskip0.35em =\hskip0.35em {P}_0-{P}_c $, with
$ \Delta P\hskip0.35em =\hskip0.35em {P}_0-{P}_c $, with ![]() $ {P}_0 $ being the pressure of outmost closed isobar and
$ {P}_0 $ being the pressure of outmost closed isobar and ![]() $ {P}_c $ being the pressure at cyclone center). Similarly, the impacts of the cyclone diameter, grade, pressure drop, and estimated central pressure on the intensity are evident from the characteristics of a cyclonic storm.
$ {P}_c $ being the pressure at cyclone center). Similarly, the impacts of the cyclone diameter, grade, pressure drop, and estimated central pressure on the intensity are evident from the characteristics of a cyclonic storm.
7. Conclusion
This study of tropical cyclone landfall prediction over the NIO demonstrates the importance of feature selection for better predictive capacity and more interpretable results that can be conducive for further inquiry on cyclone trajectory and landfall. Also, the efficacy of DRNN in processing sequential signals and time series data, requiring less number of parameters has been shown in this study. While Causality in its purest sense is a deeply philosophical paradigm, MI provides the “predictive causality” critical for analyzing the impacts of various environmental factors on a storm trajectory and intensity. The demonstrated method can be used to discover important factors in cyclone Best Track Data and study the trajectory of landfalling cyclonic storms.
Author Contributions
Conceptualization: A.M., P.M.; Data curation: A.M., P.M.; Funding acquisition: P.M.; Methodology: A.M., P.M.; Supervision: P.M. All authors approved the final submitted draft.
Competing Interests
The authors declare none.
Data Availability Statement
The Best Track Data of cyclones is available on RSMC, IMD site at https://rsmcnewdelhi.imd.gov.in/.
Ethics Statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding Statement
This research was supported by the Department of Science and Technology (DST), Government of India under the project “Machine Learning for Climate Change Analysis (MXA)” at SRIC, IIT Kharagpur.
Provenance
This article is part of the Climate Informatics 2022 proceedings and was accepted in Environmental Data Science on the basis of the Climate Informatics peer review process.





