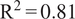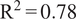Impact Statement
Ozone is a harmful air pollutant that contributes to hundreds of thousands of deaths every year. Making accurate short-term forecasts of ozone is necessary to provide the public with timely and accurate air quality warnings. We propose a forecasting system for ozone air pollution using a transformer model, a machine learning architecture that allows accurate and computationally cheap forecasts of ozone using meteorological variables as inputs. The model performs skillfully in countries across Europe, highlighting its transferability.
1. Introduction
Ozone is a secondary pollutant that is not directly emitted by anthropogenic activities but formed in the troposphere via a series of photochemical reactions (Finlayson-Pitts and Pitts, Reference Finlayson-Pitts and Pitts1997). Once formed, ozone can be transported over long distances and across continents (Lin et al., Reference Lin, Fiore, Horowitz, Langford, Oltmans, Tarasick and Rieder2015). There are a number of relationships between ozone and other variables, such as other pollutants and temperature (Laña et al., Reference Laña, Del Ser, Padró, Vélez and Casanova-Mateo2016), which are, for example, relevant for severe ozone pollution during major heat waves (Archibald et al., Reference Archibald, Turnock, Griffiths, Cox, Derwent, Knote and Shin2020). Ozone at the surface is estimated to contribute to between 365,000 and 1,100,000 premature deaths worldwide annually (Anenberg et al., Reference Anenberg, Horowitz, Tong and West2010; Silva et al., Reference Silva, West, Zhang, Anenberg, Lamarque, Shindell, Collins, Dalsoren, Faluvegi and Folberth2013; Malley et al., Reference Malley, Henze, Kuylenstierna, Vallack, Davila, Anenberg, Turner and Ashmore2017; Murray et al., Reference Murray, Aravkin, Zheng, Abbafati, Abbas, Abbasi-Kangevari, Abd-Allah, Abdelalim, Abdollahi and Abdollahpour2020), primarily by causing cardiovascular and respiratory diseases (Filippidou and Koukouliata, Reference Filippidou and Koukouliata2011; Kim et al., Reference Kim, Kim and Kim2020; Sun et al., Reference Sun, Yu, Lan, Wan, Hickman, Murulitharan, Shen, Yuan, Guo and Archibald2022). The impacts of ozone pollution have been linked to both long- and short-term exposure (Bell et al., Reference Bell, McDermott, Zeger, Samet and Dominici2004; Nuvolone et al., Reference Nuvolone, Petri and Voller2018).
Ozone air pollution is both a global and a local issue. Background levels of ozone in remote areas often exceed guidelines set by the World Health Organization (WHO), while local ozone concentrations in urban and peri-urban areas can far exceed these guidelines. The WHO estimates that 99% of the world’s population lives in areas where pollutant concentrations routinely exceed guidelines (WHO and ECE, 2021).
Due to the phytotoxicity of ozone, the negative effects of ozone air pollution on vegetation, ecosystems, and crop yields are also significant (Emberson et al., Reference Emberson, Ashmore, Simpson, Tuovinen and Cambridge2001; Fowler et al., Reference Fowler, Pilegaard, Sutton, Ambus, Raivonen, Duyzer, Simpson, Fagerli, Fuzzi and Schjoerring2009; Emberson, Reference Emberson2020). This damage leads to both considerable economic losses from reduced crop yields (Burney and Ramanathan, Reference Burney and Ramanathan2014), and the potential for increased climate change as damaged vegetation has a reduced capacity to sequester carbon dioxide from the atmosphere (Sitch et al., Reference Sitch, Cox, Collins and Huntingford2007; Ainsworth et al., Reference Ainsworth, Yendrek, Sitch, Collins and Emberson2012; Lombardozzi et al., Reference Lombardozzi, Levis, Bonan, Hess and Sparks2015; Wang et al., Reference Wang, Shugart, Shuman and Lerdau2016; Oliver et al., Reference Oliver, Mercado, Sitch, Simpson, Medlyn, Lin and Folberth2018).
There is strong evidence that ozone levels increase with increasing temperature (Porter et al., Reference Porter, Heald, Cooley and Russell2015), leading to the suggestion that under climate change, some regions will become more polluted with ozone (Bloomer et al., Reference Bloomer, Stehr, Piety, Salawitch and Dickerson2009; Rasmussen et al., Reference Rasmussen, Hu, Mahmud and Kleeman2013; Schnell et al., Reference Schnell, Prather, Josse, Naik, Horowitz, Zeng, Shindell and Faluvegi2016; Brown et al., Reference Brown, Folberth, Sitch, Bauer, Bauters, Boeckx, Cheesman, Deushi, Dos Santos and Galy-Lacaux2022), in turn leading to increased risk to human health. This effect is known as the ozone “climate penalty” (Rasmussen et al., Reference Rasmussen, Hu, Mahmud and Kleeman2013). The risks of increased ozone are compounded as extreme ozone episodes are often accompanied by high temperatures, leading to a combination of risks that further increase mortality (Dear et al., Reference Dear, Ranmuthugala, Kjellström, Skinner and Hanigan2005; Filleul et al., Reference Filleul, Cassadou, Médina, Fabres, Lefranc, Eilstein, Le Tertre, Pascal, Chardon and Blanchard2006; Lei et al., Reference Lei, Wuebbles and Liang2012). These compound events are also associated with increased levels of other pollutants, such as
![]() $ {\mathrm{PM}}_{2.5} $
, and therefore, understanding and predicting their impact is a fruitful avenue to mitigate risks to health (Galindo et al., Reference Galindo, Varea, Gil-Moltó, Yubero and Nicolás2011; Schnell and Prather, Reference Schnell and Prather2017).
$ {\mathrm{PM}}_{2.5} $
, and therefore, understanding and predicting their impact is a fruitful avenue to mitigate risks to health (Galindo et al., Reference Galindo, Varea, Gil-Moltó, Yubero and Nicolás2011; Schnell and Prather, Reference Schnell and Prather2017).
In addition to chemical effects under climate change, the lifetime of ozone, which is of the order of weeks in the free troposphere (Jacob et al., Reference Jacob, Heikes, Fan, Logan, Mauzerall, Bradshaw, Singh, Gregory, Talbot and Blake1996; Fiore et al., Reference Fiore, Jacob, Bey, Yantosca, Field, Fusco and Wilkinson2002), means that transport and meteorology are also important when determining local ozone levels (Thompson et al., Reference Thompson, Pickering, McNamara, Schoeberl, Hudson, Kim, Browell, Kirchhoff and Nganga1996; Zhang et al., Reference Zhang, Jacob, Boersma, Jaffe, Olson, Bowman, Worden, Thompson, Avery and Cohen2008). For example, transport between North America and Europe has been purported to lead to increased ozone concentrations in Europe (Li et al., Reference Li, Jacob, Bey, Palmer, Duncan, Field, Martin, Fiore, Yantosca and Parrish2002; Derwent et al., Reference Derwent, Stevenson, Collins and Johnson2004).
Regional scale features such as blocking result in extended periods of stagnant conditions, which may also lead to increased ozone (Garrido-Perez et al., Reference Garrido-Perez, Ordóñez, Garcıa-Herrera and Schnell2019; Otero et al., Reference Otero, Jurado, Butler and Rust2021). These meteorological effects typically cause changes in other environmental variables, leading to compound effects, such as the combined effect of heat waves and pollution (Li et al., Reference Li, Yao, Simmonds, Luo, Zhong and Chen2020).
In order to mitigate the impacts of ozone pollution on human health, skillful short-term forecasts of ozone concentrations, particularly at extrema, would allow preventative government policy, such as providing air quality warnings (Kelly et al., Reference Kelly, Fuller, Walton and Fussell2012; Iordache et al., Reference Iordache, Dunea, Lungu, Predescu, Dumitru, Ianache and Ianache2015). To reduce ozone concentrations, a better quantitative understanding of the causes and drivers of ozone would provide a basis for governmental interventions to reduce ozone and hence risk to human health, and provide better understanding of how ozone may evolve under changing climates (Archibald et al., Reference Archibald, Turnock, Griffiths, Cox, Derwent, Knote and Shin2020).
Due to the transport of ozone precursors and the strong diurnal cycle of ozone concentrations, it was recognized that severe ozone episodes can last for up to 8 hours. In 1997, the United States Environmental Protection Agency updated their guideline ozone metric to the daily maximum 8-hour mean concentration (DMA8) (Chameides et al., Reference Chameides, Saylor and Cowling1997; EPA U, Reference EPA1997). Since this decision, the DMA8 metric has typically been used to evaluate the risk of ozone pollution to human health and is used by the WHO to set target ozone concentrations (WHO and ECE, 2021). This metric has been found to be more strongly associated with adverse health outcomes such as respiratory and cardiovascular diseases than other metrics (Bell et al., Reference Bell, Hobbs and Ellis2005; Yang et al., Reference Yang, Yang, Guo, Wang, Xu, Duan and Kan2012; Li et al., Reference Li, Wu, Pan, Xu, Shan, Yang, Dong, Deng, Chen and Shima2018). As the most widely used daily metric for ozone, including by the WHO (WHO and ECE, 2021), it is DMA8 that we focus on.
1.1. Air pollution forecasting
Traditionally, numerical chemical transport models (CTMs) have been used for air pollution forecasting. However, these models are typically highly computationally expensive, and resolution is often an issue requiring parameterizations, which can introduce inconsistencies in model predictions (Weng et al., Reference Weng, Li, Forster and Nowack2023). Machine learning (ML) may provide a complement to existing numerical CTMs and simple statistical approaches to modeling air pollution, and climate phenomena in general, as ML allows automatic learning of the behavior of a complex system from data.
In this work, we evaluate the short-term forecasting skill of a transformer-based ML architecture across a range of European countries. The model makes 4-day forecasts of ozone in both urban and rural environments. We build on existing work by applying ML to forecast ozone air pollution, by applying a novel transformer-based method, and by evaluating the skill of the method across a wider range of test data than has been studied previously.
Previous studies focusing on forecasting surface ozone with ML have largely focused on predicting ozone in specific regions, often with relatively short time series of data. A variety of methods have been used, including bias-corrected CTMs (Neal et al., Reference Neal, Agnew, Moseley, Ordóñez, Savage and Tilbee2014; Ivatt and Evans, Reference Ivatt and Evans2020), linear regression (Olszyna et al., Reference Olszyna, Luria and Meagher1997; Thompson et al., Reference Thompson, Reynolds, Cox, Guttorp and Sampson2001), and feed-forward neural networks (Comrie, Reference Comrie1997; Cobourn et al., Reference Cobourn, Dolcine, French and Hubbard2000). More recently, recurrent neural networks (RNNs) and convolutional neural networks (CNNs) have been used in an effort to better capture spatial and temporal dependencies (Biancofiore et al., Reference Biancofiore, Verdecchia, Di Carlo, Tomassetti, Aruffo, Busilacchio, Bianco, Di Tommaso and Colangeli2015; Eslami et al., Reference Eslami, Choi, Lops and Sayeed2020; Ma et al., Reference Ma, Li, Cheng, Ding, Lin and Xu2020; Sayeed et al., Reference Sayeed, Choi, Eslami, Lops, Roy and Jung2020; Kleinert et al., Reference Kleinert, Leufen and Schultz2021). These studies illustrate the promising advances in short-term ozone forecasting possible with ML methods, in some cases outperforming state-of-the-art CTMs (Table 1).
Table 1. The relative performance of different ML and numerical approaches to ozone forecasting

Note. Methods in italics were tested on our dataset, while others used different data. The difficulty of comparing methods tested on different datasets is shown by the varying RMSE values.
To our knowledge, this is the first study that uses a purely transformer-based model to make accurate forecasts at a large number of stations across different environments and countries, and furthermore, that evaluates the capacity of an ML model to make forecasts on data drawn from countries outside the training dataset. In addition, as far as we are aware, only one other study has applied an architecture with a transformer-based component to ozone forecasting (Chen et al., Reference Chen, Chen, Xu, Sun and Peng2022).
2. Methods and Data
2.1. Model
Transformers have been shown to be highly effective in sequential domains such as natural language processing (Brown et al., Reference Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, Neelakantan, Shyam, Sastry and Askell2020; Ji et al., Reference Ji, Zhou, Liu and Davuluri2021), in part due to their ability to attend to long-term dependencies in the data. Therefore, a transformer-based model may provide an intrinsic advantage over other ML models (such as random forests) and convolutional and recurrent neural networks that have been previously explored in the ozone forecasting literature (Biancofiore et al., Reference Biancofiore, Verdecchia, Di Carlo, Tomassetti, Aruffo, Busilacchio, Bianco, Di Tommaso and Colangeli2015; Eslami et al., Reference Eslami, Choi, Lops and Sayeed2020; Kleinert et al., Reference Kleinert, Leufen and Schultz2021).
Therefore, to complement existing numerical CTMs and ML methods for ozone forecasting, we implement a state-of-the-art transformer-based deep learning architecture, temporal fusion transformer (TFT) (Lim et al., Reference Lim, Arık, Loeff and Pfister2021). The TFT combines gated residual networks, variable selection networks, a long short-term memory (LSTM) encoder–decoder layer, and multi-head attention and is described in detail in Appendix A.5.
The TFT is able to ingest both static (e.g., local population density, altitude, and landcover) and dynamic (e.g., temperature, wind speed, and cloud cover) features to make forecasts. In order to extract prediction intervals from the TFT, a quantile loss function was implemented (Appendix A.7), which provides a direct means to estimate forecast uncertainty as part of our methodology (Lim et al., Reference Lim, Arık, Loeff and Pfister2021). Where the median quantile is predicted in the quantile loss, the loss is the mean absolute error loss. The quantile loss function is described in more detail in Appendix A.7.
Despite being a relatively computationally expensive ML method, training the TFT on our dataset took less than an hour using 2 Tesla V100 GPUs. Once trained, making consecutive 4-day forecasts for a year of data across 1012 individual stations takes around a minute. This illustrates the substantial time savings compared to CTMs. Hyperparameters were optimized using Bayesian optimization, a method to robustly find optimal hyperparameters (e.g., number of layers and learning rate, as shown in Table A2) from ranges of possible values (Mockus, Reference Mockus2012). Hyperparameter optimization was carried out on a withheld validation dataset, which was then not used subsequently for model testing.
2.2. Data
The Tropospheric Ozone Assessment Report (TOAR) dataset (Schultz et al., Reference Schultz, Schröder, Lyapina, Cooper, Galbally, Petropavlovskikh, Von Schneidemesser, Tanimoto, Elshorbany and Naja2017) was selected as a suitable dataset for our forecasting model due to its global coverage and high fidelity and quantity of data, with daily measurements stretching back to the 1980s in some locations. The dataset is hosted by the Jülich Supercomputing Centre and provides around 2.6 billion observations of ozone concentrations in total.
Data from three European countries were collected: the UK, France, and Italy. These were chosen to represent three different domains in order to test whether a single model could be trained to make accurate forecasts across domains. Data from all months of the year and from urban and rural environments were included in our dataset. This dataset therefore provides a larger sample of different environments than have been studied in previous work (Biancofiore et al., Reference Biancofiore, Verdecchia, Di Carlo, Tomassetti, Aruffo, Busilacchio, Bianco, Di Tommaso and Colangeli2015; Kleinert et al., Reference Kleinert, Leufen and Schultz2021), with data from 1997 to 2014, from 1012 individual stations. Our final dataset contains more than 2 million individual days of data.
We processed the data to select features relevant to ozone to use as predictive inputs to the ML model. As the TOAR dataset is designed to include variables relevant for ozone, this streamlined data processing. The data include both static and dynamic features relevant to ozone concentrations. The static features relate to characteristics of a particular station, such as the local population density, while the dynamic features are environmental variables that change through time, such as temperature. The inputs used are described in full in Table A1. ML algorithms typically require clean datasets without missing values. We therefore removed days of data with missing values and compared summary statistics of the two datasets to ensure this did not introduce bias. Furthermore, if we had missing days of data during a particular 25-day sequence (as used for forecasting by the model), the sequence was dropped. Due to the large size and relative completeness of our dataset, imputing missing values with algorithms such as k-nearest neighbors (Batista et al., Reference Batista and Monard2002) was deemed unnecessary. By simply removing missing data, we removed the risk of bias from data imputation. All dynamic features were scaled with robust scaling (Appendix A.1), and both planetary boundary layer height and ozone were log-transformed to improve model performance (Jayalakshmi and Santhakumaran, Reference Jayalakshmi and Santhakumaran2011).
To train, validate, and test our models, we first optimized hyperparameters (e.g., number of layers and learning rate) on data from the year 2013, training on all non-test years. The computational expense of Bayesian optimization for hyperparameter tuning meant that we were limited to optimizing the hyperparameters on a single year of validation data. We then trained this fixed architecture on 5 different sets of training data using 1 year at a time as the test data (2008 to 2012) to evaluate the predictive performance of the model across a range of years. For example, when testing on 2008 data, all other years (1997 to 2014, excluding 2008 and 2013) were used as training data, and the model skill was then evaluated on 2008. The same procedure was followed for years 2008 to 2012, and then the model skill metrics were averaged across these five test years to give final model skill metrics.
This temporal splitting of data resulted in an approximately 80%-10%-10% (e.g., testing on 2012, hyperparameter optimization on 2013, and training all other years) split between training, validation, and test data. The previous 21 days of station-specific observations of ozone and dynamic covariates and 4 days of future dynamic covariate data (emulating available weather forecasts at the time) were used to make ozone forecasts up to 4 days ahead at the same station. 21 days was chosen as a suitable trade-off between computational expense and performance, retaining the capacity to account for extended air quality events. The sensitivity of using more previous time-steps of data as inputs to the model was found to be small beyond using the previous 21 days (Appendix A.2).
3. Results and Discussion
3.1. Forecasting ozone
When forecasting ozone concentrations, the TFT was skillful (MAE = 4.9 ppb,
![]() $ {\mathrm{R}}^2=0.81 $
, RMSE = 6.6 ppb, r = 0.91). These predictions, which use previous ozone observations and ERA5 meteorological reanalysis data as a proxy for both previous and forecasted meteorological data (Table A1), are therefore suitable for short-term future forecasts with meteorological forecasts as input and also for infilling missing ozone values in historical datasets.
$ {\mathrm{R}}^2=0.81 $
, RMSE = 6.6 ppb, r = 0.91). These predictions, which use previous ozone observations and ERA5 meteorological reanalysis data as a proxy for both previous and forecasted meteorological data (Table A1), are therefore suitable for short-term future forecasts with meteorological forecasts as input and also for infilling missing ozone values in historical datasets.
While we cannot make direct comparisons with all similar methods due to differing test datasets, the skill of our method compares favorably to other ML methods and numerical air quality forecasting models such as AQUM (Neal et al., Reference Neal, Agnew, Moseley, Ordóñez, Savage and Tilbee2014; Im et al., Reference Im, Bianconi, Solazzo, Kioutsioukis, Badia, Balzarini, Baró, Bellasio, Brunner and Chemel2015), especially given the size and variety of our test dataset (Table 1). In addition, a number of other ML algorithms (ridge regression, random forests, and LSTMs) were trained and tested on our data to evaluate the relative skill of the TFT.
A correlation plot of TFT predictions on the test set, against observations, is given in Figure 1a. The model was more accurate than other ML approaches such as random forests and LSTMs and approximately 40% more accurate than a persistence model (which predicts ozone as the same value as the previous day ozone) in terms of RMSE (Table 1).

Figure 1. (a) illustrates predictions against observations on 2012 test data for forecasting ozone with the TFT. The number of data points in each bin is shown by the color bar, using a log scale. (b) shows a 4-day forecast on test data at a single station. The gray line shows the attention that the transformer is paying to different days in the time history. The prediction intervals generated with the quantile loss are also shown, with the 7 different quantiles illustrated by orange shading.
We can further visualize the skill of the TFT by looking at predictions and observations at individual stations in our dataset. Figure 1b shows the previous days that the attention mechanism in the model used to inform the predictions, shown by the gray line denoting attention. The model pays attention to previous high ozone days to make future forecasts of high ozone concentrations. Similarly, when forecasting future low ozone, the model pays attention to previous days of low ozone concentrations (Figure A.6). Figure 1b also illustrates the prediction intervals generated by the quantile loss function, which are useful to evaluate trust in the model. As expected, the prediction intervals generally increase for longer lead times, as shown in Figure 4.
The TFT’s capacity to make skillful predictions of ozone concentrations at urban and rural stations (as denoted in the TOAR dataset) was also tested. The TFT performed similarly on both urban and rural data (MAE = 5.0,
![]() $ {\mathrm{R}}^2=0.81 $
and MAE = 4.8,
$ {\mathrm{R}}^2=0.81 $
and MAE = 4.8,
![]() $ {\mathrm{R}}^2=0.81 $
, respectively), which suggests that architectures of this type are able to generalize across these two environments given sufficient training data.
$ {\mathrm{R}}^2=0.81 $
, respectively), which suggests that architectures of this type are able to generalize across these two environments given sufficient training data.
As seen in Table 1, the TFT is the most skillful model on our test data, followed by the LSTM. The TFT and LSTM are designed to deal with sequential data and are able to learn from large quantities of data, which likely contributes to these models performing better than other methods. Ridge regression is a linear model that likely limits its performance; however, it is computationally cheap and provides direct interpretability. The TFT and LSTM also outperform the random forest model, a nonlinear tree-based model. While neural network models are typically not as interpretable as linear models like ridge regression, the TFT does facilitate interpretability studies that provide insight into the model’s behavior beyond what is possible in RNNs and LSTMs. Furthermore, the TFT is better adapted to ingesting static features than other machine learning methods tested.
3.2. Forecasting extreme ozone
Ozone concentrations in Europe tend to peak in spring and summer months, typically between April and June (Monks, Reference Monks2000). Making accurate forecasts of high ozone is important as these high ozone concentrations pose a great threat to health (Bell et al., Reference Bell, McDermott, Zeger, Samet and Dominici2004) and may occur more frequently in some regions in future climates (Doherty et al., Reference Doherty, Wild, Shindell, Zeng, MacKenzie, Collins, Fiore, Stevenson, Dentener and Schultz2013; Orru et al., Reference Orru, Åström, Andersson, Tamm, Ebi and Forsberg2019). We therefore evaluated the skill of the TFT during these high ozone periods. Figure 2b illustrates that the TFT was able to make reasonably skillful forecasts on spring and summertime ozone concentrations (MAE = 5.4 ppb,
![]() $ {\mathrm{R}}^2=0.64 $
). However, the performance was worse than forecasting on data from the rest of the year (MAE = 4.8 ppb,
$ {\mathrm{R}}^2=0.64 $
). However, the performance was worse than forecasting on data from the rest of the year (MAE = 4.8 ppb,
![]() $ {\mathrm{R}}^2=0.85 $
). The variability of ozone is significantly higher in spring and summer months, which makes accurate forecasting more difficult, and may require more inputs to the model, such as soil
$ {\mathrm{R}}^2=0.85 $
). The variability of ozone is significantly higher in spring and summer months, which makes accurate forecasting more difficult, and may require more inputs to the model, such as soil
![]() $ {\mathrm{NO}}_x $
emissions (Porter and Heald, Reference Porter and Heald2019).
$ {\mathrm{NO}}_x $
emissions (Porter and Heald, Reference Porter and Heald2019).

Figure 2. (a) illustrates the performance of the TFT when predicting on 2012 test data from 13 European countries unseen during training. (b) shows that when forecasting on spring and summertime test data, the performance of the TFT was poorer (MAE = 5.4 ppb,
![]() $ {R}^2= 0.64 $
) than predicting on the whole year.
$ {R}^2= 0.64 $
) than predicting on the whole year.
Furthermore, model performance across countries was evaluated during just spring (March, April, and May) and just summer months (June, July, and August). When testing across countries (Figure 3), performance in terms of mean absolute percentage error (MAPE), MAE, and
![]() $ {\mathrm{R}}^2 $
was significantly better for spring than for summer for most countries. The latitude of the country appeared to have little relationship with
$ {\mathrm{R}}^2 $
was significantly better for spring than for summer for most countries. The latitude of the country appeared to have little relationship with
![]() $ {\mathrm{R}}^2 $
or MAPE; however, unsurprisingly, MAE was higher for the countries where ozone levels are greater on average in summer. The poorer performance of the model in summer points to variables affecting ozone in summer months that are unaccounted for in the model. This could be caused by a number of factors, including the effect of biogenic VOCs (Porter and Heald, Reference Porter and Heald2019; Cao et al., Reference Cao, Situ, Hao, Xie and Li2022), or the calculation of planetary boundary layer height in the reanalysis data, as planetary boundary layer height is driven by convection, a parameterized process. For example, it has recently been shown that the European Centre for Medium-Range Weather Forecasts’ Integrated Forecast System overestimates planetary boundary layer height over the Eastern Mediterranean in summertime compared to ceilometer observations (Uzan et al., Reference Uzan, Egert, Khain, Levi, Vadislavsky and Alpert2020).
$ {\mathrm{R}}^2 $
or MAPE; however, unsurprisingly, MAE was higher for the countries where ozone levels are greater on average in summer. The poorer performance of the model in summer points to variables affecting ozone in summer months that are unaccounted for in the model. This could be caused by a number of factors, including the effect of biogenic VOCs (Porter and Heald, Reference Porter and Heald2019; Cao et al., Reference Cao, Situ, Hao, Xie and Li2022), or the calculation of planetary boundary layer height in the reanalysis data, as planetary boundary layer height is driven by convection, a parameterized process. For example, it has recently been shown that the European Centre for Medium-Range Weather Forecasts’ Integrated Forecast System overestimates planetary boundary layer height over the Eastern Mediterranean in summertime compared to ceilometer observations (Uzan et al., Reference Uzan, Egert, Khain, Levi, Vadislavsky and Alpert2020).

Figure 3. (a) illustrates the difference in performance of the model in different countries, in terms of MAE, between spring and summer, while (b) illustrates the same for MAPE. The countries are plotted by the mean ozone during spring and summer in the country.
3.3. TFT generalizes better than other ML approaches
While the improved skill of the TFT in the domain of the data it was trained on (UK, France, and Italy) is impressive, it is important for production ML models to perform accurately on data outside the country or domain that they are trained on. The TFT was not only better able to perform within the domain of its training data, it also better generalized to new domains than the other ML methods, which suggests that the model is better able to capture the underlying dynamics of the system controlling ozone concentrations (Table 2). To evaluate the skill of our model in generalizing to unseen data, we deployed the model, trained solely on data from the UK, France, and Italy, to make forecasts in a separate test set comprising 13 other European countries with the same covariates. The model was able to generalize impressively on data from these unseen countries when evaluated on a single year of test data (
![]() $ {\mathrm{R}}^2=0.78 $
, MAE = 5.0 ppb, RMSE = 6.6 ppb), as shown in Figure 2a. This suggests that the model could act as a Europe-wide predictive model, without requiring retraining. The predictive uncertainty for the model on the unseen countries was marginally wider but, similar to the training countries, was in line with the skill of the predictions. Furthermore, the predictive uncertainty was reasonably well calibrated with the accuracy of the model—in countries where the model performed poorly, the predictive uncertainty was larger (Figure 4).
$ {\mathrm{R}}^2=0.78 $
, MAE = 5.0 ppb, RMSE = 6.6 ppb), as shown in Figure 2a. This suggests that the model could act as a Europe-wide predictive model, without requiring retraining. The predictive uncertainty for the model on the unseen countries was marginally wider but, similar to the training countries, was in line with the skill of the predictions. Furthermore, the predictive uncertainty was reasonably well calibrated with the accuracy of the model—in countries where the model performed poorly, the predictive uncertainty was larger (Figure 4).
Table 2. The relative performance of different ML approaches to ozone forecasting for different domains within our data

Note. The values show the ability of the LSTM and the TFT to generalize well to new countries across Europe, while other methods fail to generalize as effectively. Detailed results for each testing country are available in Appendix A.3.

Figure 4. (a) shows the width of prediction intervals generated by the model on the test data for the countries used for training (UK, France, Italy) and for test data from the unseen European countries. The prediction intervals are marginally wider for the unseen countries, in line lower model performance in these countries. (b) illustrates that the prediction intervals increase as the MAE of the predictions increases, consistent with well-calibrated prediction intervals.
In previous work, when testing in a new domain, the similarity of the domain to the training domain appeared to significantly affect performance. This is likely due to correlations learned from the training set that do not hold in the new domain, or country. Such inconsistencies in the relationships point to an issue related to the models being able to identify the generic causal drivers of ozone, rather than spurious correlations specific to individual locations (Runge et al., Reference Runge, Nowack, Kretschmer, Flaxman and Sejdinovic2019). At least, we empirically find that the TFT performance is more robust to being deployed away from its spatial training domain than, for example, random forest models, which often poorly generalize to out-of-distribution data. We highlight this important result for two of the unseen European countries, Spain and Poland, to illustrate the relative skill in terms of
![]() $ {\mathrm{R}}^2 $
different methods in Figure 5a.
$ {\mathrm{R}}^2 $
different methods in Figure 5a.

Figure 5. (a) shows the accuracy of different ML methods on the test data for the countries used for training (UK, France, Italy) and for a pair of unseen countries (Spain and Poland). The performance of the LSTM and the TFT is relatively stable when forecasting in new countries, while the random forest and ridge regression models perform poorly. (b) shows a density plot of ozone concentrations observed in the test data for the countries used for training (UK, France, Italy) and for 2 of the 13 unseen test countries (Spain and Poland).
4. What is the TFT Paying Attention To?
We extracted feature importances, derived from the weights of attention mechanism in our ozone forecasting model, to examine which dynamic features are the most important for the model when making forecasts with our data (Figure 6). These importances correspond well with expected physical drivers: Both temperature and planetary boundary layer height are key variables (Porter and Heald, Reference Porter and Heald2019). The skillful performance of the TFT suggests that good forecasting skill can be achieved with only the meteorological variables used by the model, which may simplify implementation of this method operationally, similar to recent results using random forests (Weng et al., Reference Weng, Forster and Nowack2022). Static feature importances are shown in Figure A.7. When training and testing the model without static features, we found only slight degradation of model performance (
![]() $ {\mathrm{R}}^2=0.81 $
, MAE = 5.0 ppb, RMSE = 6.7 ppb), suggesting that the inclusion of these variables is not essential for high model skill, further simplifying operational implementation.
$ {\mathrm{R}}^2=0.81 $
, MAE = 5.0 ppb, RMSE = 6.7 ppb), suggesting that the inclusion of these variables is not essential for high model skill, further simplifying operational implementation.

Figure 6. The variable importances of the TFT when making forecasts, derived from the weights of the attention mechanism. These are largely in line with expected physical relationships.
5. Conclusions
Despite decades-long model development, ozone remains challenging to forecast with existing numerical methods. Our ML model, the TFT, makes skillful forecasts of ozone concentrations at stations across Europe. The model requires only static features and dynamic variables available from weather forecasts and could therefore feasibly be used operationally to forecast ozone at observational stations. The model is able to make accurate forecasts across environments and performs reasonably well when predicting extrema. The model is able to generalize well to data from 13 European countries unseen in training, outperforming other ML methods in these new domains. This suggests, in combination with feature importances, that the model is learning sound physical relationships in the data. The model provides a promising, computationally cheap method to make accurate forecasts of ozone across Europe.
However, further work is required to ensure the model can make accurate predictions of extrema, such as explicitly encoding known physical relationships in the model, and furthermore that operational forecasts at short lead times can be used instead of reanalysis data. In addition, while we have demonstrated that the model generalizes well to other European countries, it would be a worthwhile question to explore how far the model can be taken across to countries and world regions with even more pronounced differences in meteorology and emission regulations. However, an initial extension of this work could be to evaluate the skill of the model in locations with similar ozone levels and meteorological conditions, such as other regions in the Northern Hemisphere midlatitudes.
Acknowledgments
The authors thank the NERC Earth Observation Data Acquisition and Analysis Service (NEODAAS) for access to compute resources and staff support for this study and the TOAR database maintainers.
Author contribution
Formal analysis: S.H.M.H; Investigation: S.H.M.H. and P.T.G.; Methodology: S.H.M.H, P.T.G., P. J. N., and A.T.A.; Software: S.H.M.H; Visualization: S.H.M.H., P.T.G., P.J.N., and A.T.A.; Writing—original draft: S.H.M.H.; and Writing—review and editing: S.H.M.H., P.T.G., P.J.N., and A.T.A.
Competing interest
The authors declare none.
Data availability statement
The TOAR dataset is publicly available online (https://join.fz-juelich.de/services/rest/surfacedata/, last accessed 22/08/2023) (Schultz et al., Reference Schultz, Schröder, Lyapina, Cooper, Galbally, Petropavlovskikh, Von Schneidemesser, Tanimoto, Elshorbany and Naja2017), and the code of this work is available at https://github.com/shmh40/forecasto3 (last accessed 22/08/2023).
Ethics statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
S.H.M.H. acknowledges funding from EPSRC via the AI4ER CDT at the University of Cambridge (EP/S022961/1) and support from The Alan Turing Institute. P.T.G. and A.T.A. were financially supported by NERC through NCAS (R8/H12/83/003). P.N. was supported by the Natural Environment Research Council (grant no. NE/V012045/1).
A. Appendix
A.1. Features from the TOAR dataset
Table A1 describes the data used as features for the machine learning model. The features are split into static and dynamic features. Static features describe the characteristics of a particular station, while dynamic features vary through time. Due to the large size and relative completeness of our dataset, imputing missing values was deemed unnecessary, and rows with missing data were dropped. The way these features are ingested by the TFT are described by Figure A.4. The static features are used as shown, and the dynamic features (apart from ozone) are treated as known future inputs. The reanalysis data are taken in this case to be a proxy for a meteorological forecast, which would be used operationally. All features were scaled with robust scaling (Equation A.1), following testing with standard and min–max scaling on the validation data. Ozone was log-transformed, as was planetary boundary layer height, which improved model performance.
Table A1. Relevant data extracted from the TOAR database

A.2. Model hyperparameter optimization
Table A2 details the hyperparameters used for the TFT model. These hyperparameters were determined with Bayesian optimization, implemented with weights and biases (Biewald, Reference Biewald2020). Bayesian optimization is a method used to determine the optimal hyperparameters of a model, by defining a Gaussian process that describes the function controlling the performance of the model with respect to the hyperparameters. This function is evaluated and updated as the hyperparameter space is explored, as shown in Figure A.1. We found that the most influential hyperparameters were the learning rate and the choice of optimizer. Furthermore, we also evaluated the optimal number of past time-steps necessary for skillful prediction. While increasing the number of past time-steps past 21 days did improve performance marginally, there was little improvement relative to the increased computational burden. Additionally, decreasing the number of time-steps below 21 days did hinder performance considerably, especially at very low numbers (fewer than 5 days). The hyperparameters of the ridge regression, random forest, and LSTM models were optimized with grid search.

Figure A.1. Plot illustrating the hyperparameter optimization and the skill, in terms of the loss on the validation data, of various hyperparameter combinations for the TFT.
Table A2. Hyperparameters for the final TFT and LSTM models used for model evaluation

Note. We carried out 120 runs of Bayesian optimization for the TFT.
A.3. Performance across countries
The performance of the optimized model in forecasting
![]() $ {\mathrm{O}}_3 $
in different countries is given in Figure A.2 below. While some European countries had very little data available, others provided a good quantity of data. Performance is relatively good across countries, with some poorer skill in Norway (which has little data) and Portugal.
$ {\mathrm{O}}_3 $
in different countries is given in Figure A.2 below. While some European countries had very little data available, others provided a good quantity of data. Performance is relatively good across countries, with some poorer skill in Norway (which has little data) and Portugal.

Figure A.2. Plots illustrating the skill of the model in predicting ozone in different countries across Europe.
A.4. Comparison of model performance in spring and summer across countries
To evaluate the processes that might be poorly represented by our model, we tested the trained model across all countries, using just spring and then just summer data. We found that in general, the model performance was poorer in summer than in spring. Furthermore, we found that there was little correlation between the latitude of the country and the difference in performance between spring and summer. The findings are described in Figure 3; however, an analysis of the spring–summer difference in just the UK, France, and Italy dataset is provided in Figure A.3. In terms of RMSE and MAE, we found the performance of the TFT was better in spring but poorer in terms of
![]() $ {\mathrm{R}}^2 $
.
$ {\mathrm{R}}^2 $
.

Figure A.3. (a) Performance of the TFT when predicting on 2012 spring test data from the UK, France, and Italy. (b) Performance of the TFT when predicting on 2012 summer test data from the UK, France, and Italy.
A.5. Architecture of the temporal fusion transformer
The temporal fusion transformer (Lim et al., Reference Lim, Arık, Loeff and Pfister2021) is designed to carry out multi-horizon (multiple time-step) forecasting of a target variable using both static and dynamic covariates. The fundamental setup of this forecasting task is described in Figure A.4. Both dynamic and static inputs are passed to the model, which then makes forecasts.

Figure A.4. Setup of a typical multi-horizon forecasting problem. Source: ’Temporal Fusion Transformers for interpretable multi-horizon time series forecasting’, Lim et al. (Reference Lim, Arık, Loeff and Pfister2021), licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).
The TFT is an attention-based ML model that uses the attention mechanism (Vaswani et al., Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017) to learn long-term dependencies in data, combined with recurrent layers to learn short-term dependencies. The TFT also deploys gating layers to minimize the effect of less relevant predictors. The architecture of the model is given in Figure A.5.

Figure A.5. Architecture of the temporal fusion transformer model. The model consists of a combination of RNN encoders, followed by an attention layer, and then a fully connected decoder layer. Source: ’Temporal Fusion Transformers for interpretable multi-horizon time series forecasting’, Lim et al. (Reference Lim, Arık, Loeff and Pfister2021), licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).
As described in Lim et al. (Reference Lim, Arık, Loeff and Pfister2021), the TFT offers a number of key features to improve upon existing models for multi-horizon forecasting.
The first is the use of gated residual networks (GRNs) to suppress nonlinear relationships in the model. Variable selection networks are deployed to identify and reduce the effect of poor predictors. Inputs are passed first through a GRN, followed by a Softmax layer, a function that converts the output vector to a probability distribution, to yield weights describing how relevant a feature is for predicting an output. The original features are then weighted by the variable selection weights to yield appropriately weighted features. Static covariates (the covariates which do not vary through time, such as landcover), are encoded with GRNs to produce 4 context vectors, which are then combined with the dynamic features. The TFT then uses a long short-term memory network (LSTM) encoder–decoder to provide an alternative to the positional embeddings used in traditional transformer architectures. The context vectors from the static covariates are used to initialize the cell and hidden state (a representation of the previous data in the sequence seen by the model) in the first LSTM in the layer.
The TFT then uses multi-head attention, as detailed in Vaswani et al. (Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017), which allows the model to learn long-term dependencies in data. The weights of the attention mechanism allow us to interpret that features and previous time-steps that are the most important for prediction, aiding model interpretability. The decoder deploys masking to ensure that it can only attend to features preceding it. The outputs from the attention layer are then passed to a feed forward GRN, which also takes inputs via a gated residual connection that skips the attention layer providing a simpler model if the attention layer is unnecessary for accurate predictions (this behavior is learned during training), as shown in Figure A.5. Finally, prediction intervals from the outputs of the final GRN are generated by making predictions at different quantiles, using a linear transformation of the output.
The TFT is trained by minimizing the sum of the quantile loss across quantile outputs.
A.6. Attention in the temporal fusion transformer
The attention values in the TFT are calculated as in Lim et al. (Reference Lim, Arık, Loeff and Pfister2021). In the TFT architecture, standard multi-head attention is additively aggregated to interpretable multi-head attention. In this formulation, each attention head learns different temporal relationships from the same set of input features, and then the aggregation of these attention weights can be viewed as an ensemble, allowing interpretability studies. We refer the reader to Lim et al. (Reference Lim, Arık, Loeff and Pfister2021) for full details.
In the context of this study, we generally see that the model, as expected, pays more attention to the more recent past days when making future forecasts and that the model is able to attend to recent low days of ozone when making forecasts of low ozone and, similarly, to recent days of high ozone when forecasting future high ozone.

Figure A.6. Left-hand plot shows the attention paid to different days in the past, averaged over the whole test set. The right-hand plot illustrates an example of the model attending to previous low ozone days when making forecasts of future low ozone. This example is from a station in one of the unseen countries.
Since the attention values for the dynamic and the static features are calculated separately, we include the feature importances for the static variables here.

Figure A.7. Plot illustrating the feature importances for the static features.
A.7. Quantile loss
The quantile loss function is used in this work to extract prediction intervals from the TFT model. The quantile loss function is given as follows:
where
![]() $ {(.)}_{+} $
is equal to
$ {(.)}_{+} $
is equal to
![]() $ \mathit{\max}\left(0,.\right) $
(Wen et al., Reference Wen, Torkkola, Narayanaswamy and Madeka2017). Note that when q = 0.5, the quantile loss is the same as using the mean absolute error loss function. The model is trained to find the weights of the model that minimize the total loss of the quantile loss over various values of q for various prediction horizons.
$ \mathit{\max}\left(0,.\right) $
(Wen et al., Reference Wen, Torkkola, Narayanaswamy and Madeka2017). Note that when q = 0.5, the quantile loss is the same as using the mean absolute error loss function. The model is trained to find the weights of the model that minimize the total loss of the quantile loss over various values of q for various prediction horizons.
A.8. Benchmark models
We used 4 other approaches to compare with the TFT. The first of these is a persistence model, which simply predicts the next timestep of ozone to be equal to the previous time-step. This provides our baseline model.
We also evaluated a ridge regression model. Ridge regression (Tikhonov regularization) is often deployed in multiple regression tasks where covariates are correlated.
Ridge regression uses the
![]() $ {\mathrm{L}}_2 $
penalty on the coefficients of the model, similar to LASSO regression, which uses the
$ {\mathrm{L}}_2 $
penalty on the coefficients of the model, similar to LASSO regression, which uses the
![]() $ {\mathrm{L}}_1 $
penalty. Ridge regression is a standard benchmark used in the environmental sciences but is a linear method, which limits its flexibility.
$ {\mathrm{L}}_1 $
penalty. Ridge regression is a standard benchmark used in the environmental sciences but is a linear method, which limits its flexibility.
Random forests are a widely used nonlinear ensemble machine learning technique, which construct multiple decision trees during training, using bootstrap aggregating (bagging) to reduce instability during training. Bagging generates new training datasets from the original training data by sampling from the original data, with replacement. Decision trees are then trained on these new training sets, and the output of the model is determined by aggregating the predictions of the individual trees on the new training datasets. Random forests are prone to overfitting training data, which can lead to poor out-of-distribution performance.
While random forests are a nonlinear model and therefore may be able to better fit data with nonlinear relationships, they do not necessarily exploit temporal dependencies in data well.
Long short-term memory networks are a form of recurrent neural network that have been shown to perform very well on time series data, aided by the use of memory cells which improve on vanilla recurrent neural networks. However, recent work in fields such as natural language processing has illustrated that transformers perform better on sequential data, in part due to their capacity to model long-term dependencies in data. Furthermore, the temporal fusion transformer is adapted to ingest both static and dynamic features, unlike the other models, which provides a small improvement in model skill.