INTRODUCTION
The topology of contacts in host organisms is known to be an important influencing factor in infectious disease dynamics. It has been argued theoretically that highly connected individuals play a pivotal role in disease spread and that they have a strong impact on both individual risks of infection as well as spread dynamics at the level of entire populations [Reference Bansal, Grenfell and Meyers1–Reference Pastor-Satorras and Vespignani3]. Furthermore, it has been shown that both the clustering of contact partners and repeated contact with the same person can slow down an outbreak compared to the dynamics of an otherwise identical random mixing model [Reference Smieszek, Fiebig and Scholz4, Reference Szendrói and Csányi5].
Empirical data on host-to-host contacts is needed to complement the theoretical knowledge concerning the importance of network topology for infectious disease dynamics. Methods have been developed to measure potentially contagious contacts in real-world settings. Currently, the dominant approach for measuring epidemiologically relevant contact data is contact diaries [Reference Mikolajczyk6–Reference Horby12]. Empirical research on potentially contagious contacts, particularly the highly cited study by Mossong et al. [Reference Mossong8], has influenced the discussion on the patterns and risk factors of disease spread and has informed infectious disease modelling [e.g. Reference Smieszek13]. In addition, various studies have shown that empirical contact data can successfully be applied in epidemiological models to replicate serological data [Reference Goeyvaerts14–Reference Wallinga, Teunis and Kretzschmar16].
Despite the increasing use of diary-based contact data for understanding and explaining infectious disease dynamics, few studies have addressed the quality and appropriateness of this methodological approach. One study compared retrospective and prospective study designs and found ‘only minor differences in the number of contacts, with on average more contacts reported in the prospective survey’ [7, p. 133]. Another study compared a web-based mode of data collection with a diary-based one and concluded that the diary-based approach is less demanding and better suited for collecting detailed data than the web-based approach [Reference Beutels9]. A similar result was reported in a study that compared paper-based diaries with data collection via personal digital assistants (PDAs) [Reference McCaw10]. Here, the classical diaries were also perceived to be easier to use. However, there is still a lack of research that aims to measure errors and biases related to the diary approach directly, and not only the differences between variations of the same method.
The goal of our research was to develop a study design that allows the measuring of reporting errors and biases related to contact diaries in a more encompassing and complete manner than previous studies. This paper provides first answers to the questions of (i) how important measurement errors related to the diary method are, (ii) how reporting errors are related to the duration of a contact, and (iii) how reporting errors are related to the total number of different contact partners during a day. Further, we analysed whether the participants showed fatigue during the later study days. We focused solely on contacts that are relevant for the spread of pathogens that are transmitted via direct, non-sexual contact between hosts.
METHODS
Study design and data collection
Typically, diary-based studies are designed as so-called egocentric network studies. That means, the participants are chosen randomly, or using any other appropriate sampling scheme, typically from a large population; the participants (egos) report information about their contact partners (alters), but these alters are not usually participants in the study. Thus, it is not possible to link up the participants of an egocentric network study with each other in order to achieve a complete network structure. Another drawback of the purely egocentric network design is that there are limited possibilities for validating the answers of the participants (e.g. by utilizing the symmetry condition for age-structured contact matrices, as done by Wallinga et al. [Reference Wallinga, Teunis and Kretzschmar16]). Consequently, the participants' answers are usually taken for granted.
To overcome the methodological limitations of egocentric network studies and to be able to give answers to the posed research questions, we conducted an empirical network study with a complete network design (i.e. the alters of an ego are also participants in the study, and they can be linked). Our target population consisted of the employees of three research groups belonging to a single institute at ETH Zurich. In total, 50 employees agreed to participate and actually participated in our study. The data collection started on Monday, 17 May 2010, and ended on Friday, 21 May 2010.
The participants of our study were asked to report only potentially contagious contacts they had with other participants of this study. A potentially contagious contact was defined as (i) a conversation held at <2 m distance and with more than ten words spoken, or as (ii) any sort of physical contact with a person. When a contact event in keeping with this definition occurred with any other participant of the study, both involved participants were asked to note the respective alter's name in their diaries and an estimation of the total time of contact during the entire day (in 5-min intervals).
All participants were asked to complete their diaries independently and not to communicate with the other participants about the contents. Thus, if all participants perceived and recalled all contacts correctly, there would be a mirror-inverted – but otherwise totally identical – match for every reported contact in the database. As a consequence, our study design allows investigation of the accuracy with which contact diaries measure potentially contagious contacts, because every deviation from the aforementioned ideal indicates a reporting error.
Analyses of errors and biases
Although the chosen study design allows the investigation of reporting errors in contact diary studies, even this design results in unidentified contacts whenever both involved participants do not report a common contact that actually took place. However, with few assumptions it is possible to approximate the number of completely unreported contacts as well as the probability of reporting a contact or of forgetting to report a contact in a particular setting. In the following text we present a mathematical approach for doing so, and describe how we assess the uncertainty of these approximations by means of bootstrapping.
The probability of forgetting to report a contact most likely depends on many factors, such as the duration and the intensity of the contact, the traits and the intra-individual variation of the motivation of the involved participant, as well as the context in which the contact takes place. Controlling and investigating all of these factors requires large datasets and complex study designs, which makes it difficult to convince target groups to participate. Thus, we concentrate on one of the supposedly most influential factors, i.e. contact duration, and analyse how reporting behaviour depends on a contact's duration.
We introduce the following simplifying assumptions and conventions as a prerequisite for approximating the probability of reporting a contact of a certain duration, P, as well as the number of completely unreported contacts: (i) the recall bias depends only on the duration of the contact and not on the characteristics of the involved participants or the context; (ii) the reports of the participants are stochastically independent; (iii) in any matching pair of contact reports, the duration with the higher value is assumed to be the true duration; (iv) contacts can be forgotten, but no contacts are reported that did not occur in reality.
Under these assumptions, the problem can be represented by a unit square (see Fig. 1) for all four duration categories. In this unit square, N 1 is the number of contacts with the duration of interest that were reported by both participants. N 2 is the number of contacts reported by participant 1, but not by participant 2. N 3 is the number of contacts reported by participant 2, but not by participant 1. We assumed here that all participants report contacts of a certain duration with the same probability [assumption (i)]. Accordingly, N 2 and N 3 can be derived from the total number of contacts reported by just one participant, N 2+3, by using the relation N 2+3=2N 2=2N 3. X is the unknown number of contacts that were reported neither by participant 1 nor by participant 2. Due to assumptions (i) and (ii), the probability of reporting a contact, P, is defined as P=N 1/(N 1+N 2)=N 1/(N 1+N 3) and the probability of forgetting to report a contact is given by the complementary probability Q=1–P.
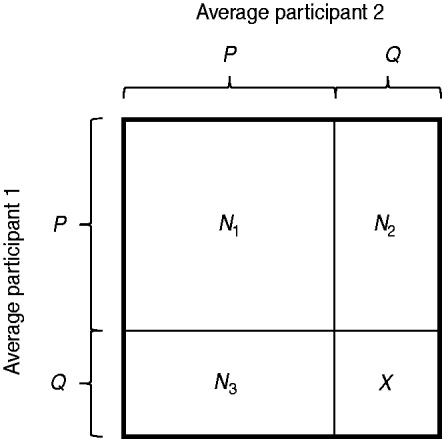
Fig. 1. Unit square representation of all possible combinations of reporting behaviour. P is the probability of reporting a specific contact (assumed to be equal for all participants). Q is the probability of not reporting the contact. N 1 is the number of contacts that were reported by both involved participants. N 2 and N 3 stand for the those contacts that were reported only by one participant. X is the number of contacts that were reported by none of the involved participants.
We assessed the uncertainty of our approximations by bootstrapping. To this end, 1000 resamples were constructed from the original sample and the probabilities P and Q were calculated for each of these resamples. Therefore, for all resampled participants, we added up (i) the numbers of contacts reported mutually by all egos and their alters, as well as (ii) the numbers of contacts that were only reported by the alters. Then, P is defined as the sum of all mutually reported contacts divided by the total of both sums. We used the mean, the 0·025 quantile (referred to as lower quantile) and the 0·975 quantile (referred to as upper quantile) as indices for describing the distribution and uncertainty of our approximations.
Statistical relationships between different variables were analysed with standard statistical tools such as the χ2 test and linear regression analysis.
RESULTS
Descriptive characterization of the contact data
A total of 623 instances of contact were reported: 405 (65·0%) of which were reported by both involved participants and 218 (35·0%) were reported by only one participant and, thus, had no match (a list of all reported contacts is provided in the Supplementary online material, contact_data.csv). The cumulative distribution of contact duration is as follows: for 31·1% of all individual contact reports, a duration of ⩽5 min was listed; for 51·6% of reports, ⩽15 min was listed; for 69·2%, ⩽30 min; for 75·4%, ⩽45 min; and for 87·1%, ⩽1 h. The longest reported contact duration was 8 h. Most (90·0%) of all valid reports asserted that the respective contact with a certain alter was only conversational. Only 10·0% of all individual contact reports included physical contact.
Congruence between contact reports
For every matching pair of reported contacts, Table 1 shows whether or not the respective estimates of the contact duration were in accord with one another. For Table 1, we recoded the duration estimates of the participants into the time categories used by Mossong et al. [Reference Mossong8], Mikolajczyk et al. [Reference Mikolajczyk6], Horby et al. [Reference Horby12], and Smieszek [Reference Smieszek11]. In this table, the higher duration estimate (columns) was cross-tabulated against the lower duration estimate (rows). In the case of contacts that were only reported by one contact partner, we took the existing duration estimate as the higher estimate and introduced missing second reports of contact as the lowest category for the lower duration estimate. When analysing the correspondence of the duration categories of all matching pairs of contact reports, we see that not only 57·8% of all reports were recoded into the same duration category and that 33·5% of all pairs were allocated to adjacent duration categories, but also that 8·8% differed by two or more time categories.
Table 1. Cross-tabulation of pairs of duration estimates

* For every contact that was reported in this study, there is information regarding the existence and duration of this respective contact from two participants. This table shows a cross-tabulation of the higher contact duration estimate vs. the lower duration estimate of every reported contact. If just one participant reported the contact, then the lower value is set to ‘not reported’.
† ‘Not valid’ indicates that the contact was reported, but no information or not-interpretable information about the duration was provided by one participant.
‡ There were four contacts that were reported only by one involved participant, but without information on the duration.
Table 2 shows a cross-tabulation of the kinds of contact for matching pairs of reported contacts. We classified contact events including physical contact as more intense than purely conversational contacts – regardless of the contact's duration. Table 3 has the same layout as Table 1; however, it includes only those contacts that were reported, at least by one of the involved participants, to have included physical contact. As the number of reports including physical contact is very low, we decided not to further analyse the impact of the reported kind of contact on the reporting behaviour.
Table 2. Cross-tabulation of pairs of reports on kind of contact

* This table shows a cross-tabulation of the more intense contact report vs. the less intense report. If just one participant reported the contact, then the lower value is set to ‘not reported’.
† ‘Not valid’ indicates that the contact was reported, but no information or not-interpretable information about the intensity of the contact was provided by at least one involved participant.
‡ There were 11 contacts that were reported by only one participant, but without information on the intensity of the contact.
Table 3. Cross-tabulation of pairs of duration estimates (only events including physical contact)

* This table shows a cross-tabulation of the higher contact duration estimate vs. the lower duration estimate of every reported contact, but only those contact reports are included for which at least one participant stated that physical contact took place. If just one participant reported the contact, then the lower value is set to ‘not reported’.
Reporting behaviour by duration category
The descriptive data shown in Table 1 suggests that problems recalling contacts occur more often in the case of short encounters than in the case of long-lasting interactions. This is further confirmed by the results of a χ2 test for independence between contact duration (four categories as defined in Table 1) and reporting behaviour (contact reports by both contact partners vs. just by one contact partner), which rejects the null hypothesis that there is no relationship between these two variables with χ2(3)=134·3 (P<0·001).
According to our calculations, the probability P of reporting a contact is 49·0% [bootstrapping interquantile interval (BIQI) 39·8–58·3] if contact duration is reported to be between 1 and 5 min; 81·0% (BIQI 75·4–88·8) for 6–15 min; 89·0% (BIQI 84·6–93·1) for 16–60 min; and 95·2% (BIQI 92·0–97·9) for contacts >1 h. Thus, we expected that more than one quarter of contacts lasting ⩽5 min were not reported at all, and less than 4% of contacts lasting between 6–15 min (Supplementary online material, section 1).
Self-reported vs. total number of contacts
We further analysed the relationship between the total number of contact partners attributed to a participant during the course of the study week (i.e. the number of set elements in the union of the contacts reported by an ego or its alters; N 1+N 2+N 3 in Fig. 1) and the actual number of contact partners reported by this participant (N 1+N 2). The relationship can be well described with a linear model: a linear regression analysis with the total reported number of contact partners as the independent variable, the self-reported number of contact partners as the dependent variable, and a forced intercept of zero (i.e. the regression line had to go through the origin) resulted in a slope of 0·83 with an explained variance R 2=97·7 (the regression diagnostics are shown in the Supplementary online material, section 3).
Fatigue effects
Figure 2 shows the mean, the lower and the upper quantile for the probabilities of reporting a contact, P, calculated separately for all four duration categories and for all 5 days of the working week by means of bootstrapping. A decline in the reporting accuracy over time can be caused by fatigue. In the case of short contacts (1–5 min), the average P is between 50% and 60% on Monday and Tuesday; it drops below 40% on Wednesday and Thursday; however, the highest average P is 76·7% on Friday. In the case of all other duration categories, there appears to be a trend that P declines over the course of the week.

Fig. 2. Mean (grey bars), and upper and lower quantiles (whiskers) of the probabilities of reporting a contact by day of the week (calculated by bootstrapping). Indices for contacts of duration of (a) ⩽5 min; (b) 6–15 min; (c) 16–60 min; (d) >1 h.
DISCUSSION
Interpretation of the results
On the basis of our analyses and the feedback we received from our participants, we interpret and discuss the results as follows:
(1) The overall level of reporting errors using the diary approach is rather high. More than one third of all reported contacts were only reported by one participant. While our study design allows us to reconstruct those – presumably forgotten – contacts of an ego which are reported by the alter, in the common egocentric study design, this information is lost.
(2) We found the number of contact partners reported by a certain ego (N 1+N 2 in Fig. 1) to be approximately proportionally related to its total reported number of contact partners (N 1+N 2+N 3). This finding is in accord with other research on recall bias in network research [Reference Mikolajczyk and Kretzschmar7, Reference Brewer and Webster17, Reference Brewer, Garrett and Kulasingam18] and with our other datasets (T. Smieszek, J. Maag and L. Muggler unpublished findings). That means that there is higher underreporting for highly connected individuals than for rather isolated individuals. While for some research questions and methodologies this bias might be unproblematical, other findings might be highly affected by it. For instance, Mikolajczyk & Kretzschmar [Reference Mikolajczyk and Kretzschmar7] argue that for models based purely on the relative average contact frequency differences between age groups, this bias is irrelevant (see discussion on p. 133 of their paper). However, their argument is only correct if age is not correlated with other predictors for reporting errors, such as the duration of the contacts.
(3) It is likely that the proportional relationship between the total and the self-reported number of contacts we found only holds true for a limited range of contact partners. The maximum number of contact partners at work during one day reported in this study was 16. It is plausible to assume in cases of much higher contact numbers (e.g. from a train conductor or flight attendant), that individuals would either deny their participation or would report disproportionally fewer contact partners. Furthermore, there is evidence that the proportion of short and non-intense contacts increases with the total number of contact partners [Reference Smieszek11]. If highly connected individuals show disproportionately high numbers of short contacts, they are also likely to particularly suffer from difficulty recalling the contacts they had.
(4) The underreporting of contacts in diary-based datasets is highly correlated with the duration of a certain contact. We estimate that the probability of forgetting a contact that lasts ⩽5 min is more than 50%. In contrast, contacts that last >1 h have an estimated probability of about 5% of going unreported. This finding, that deficient recall depends on measures of contact intensity, is intuitively plausible: short encounters are, in many cases, accidental and of rather low importance for the involved individuals. Humans tend to remember events that have a high emotional or resource involvement better than they do short and unimportant occurrences. This systematic bias might particularly affect research that builds upon intensity-differentiated contact data [e.g. Reference Smieszek11].
(5) Finally, in longitudinal studies like ours, fatigue effects might occur and can be a relevant influence factor on the number and kind of reporting errors. McCaw et al. searched for fatigue effects in their contact data with two different analyses: they found no evidence that the sequence of the different modes of data collection influenced the reporting quality, but within a particular mode the number of reported contacts declined with time [Reference McCaw10]. It is difficult to interpret our data with respect to fatigue effects as – due to the study design – it is inherently impossible to distinguish the effects of the specific peculiarities of a certain study day from fatigue: it seems plausible to us that the pronounced fall in reporting accuracy on Wednesday was caused by a particularly strenuous workload for one research group on that day, while the fact that many study participants work at home on Fridays might explain that day's above-average accuracy in reporting contacts lasting between 1 and 5 min. Considering that it was not possible to control for the impact of the particular study day, the decline of the probabilities towards the end of the week still suggests that there might be a slight fatigue effect.
Limitations of the study
Caution should be exercised when generalizing our findings because they are based on a small, specific group of participants (academically trained people) within a specific setting (scientists working for a university). Although the office setting found in a university is typical of many professions, the results of an analogous study with other participants and another setting might differ. Although we deem it plausible that the general effects found in this study are also true for other groups, more studies on different groups are needed to achieve a more robust picture on the errors in diary-based contact data.
Furthermore, our data did not allow us to analyse and to control for all potentially relevant determinants of reporting behaviour. We assumed, for instance, that participants in a contact study do not differ in their reporting probabilities. In reality, participants in such studies differ in their motivation as well as in their cognitive abilities. In principle, it is possible to calculate the individual probabilities of reporting a contact by applying the unit square (Fig. 1) to all possible combinations of individuals (Supplementary online material, section 2). However, the theoretical maximum of reported contacts per pair of participants is specified by the number of study days, because the usual contact definition relies on the accumulated time of interaction during an entire day. In our study, there are at maximum five contact reports per pair of individuals. On one hand, such low numbers do not allow robust estimates of P 1 and P 2. On the other hand, it is not feasible to conduct longitudinal contact diary studies that last much longer, because in that case many people would refuse to participate.
We believe that most unmatched contact reports are the result of underreporting. In principle, it is also possible that contacts are reported that have either not occurred or that do not fall under the given definition of a potentially contagious contact. Some participants mentioned difficulties in deciding whether a certain interaction occurred at a distance of less than or more than 2 m. They mentioned particular difficulties with accurately reporting interactions that took place during meetings or social gatherings. It is further possible that participants of such a study do not understand the contact definition correctly, which also might result in over- or underreporting of contacts.
CONCLUSION
To conclude, it can be stated that diary-based contact data is more appropriate for certain types of analyses and for certain host–pathogen systems than it is for others. The contact diary approach is probably problematical for detailed investigations of the spread dynamics of highly contagious diseases (e.g. typical childhood diseases such as Bordetella pertussis). In the case of such host–pathogen systems, even minor contact is sufficient to transmit infection. Since such contacts are particularly affected by the described biases, it is likely that a large proportion of important contact information is missing in diary-based datasets.
The opposite is true for host–pathogen systems in which transmission takes place through long and intense interaction (e.g. Neisseria meningitidis or Staphylococcus aureus) and which often achieve only low to medium basic reproduction numbers. Here, the contact topology greatly influences spread dynamics [Reference Smieszek, Fiebig and Scholz4] and, at the same time, contact diary-based data is likely to be more accurate than in the case of highly contagious infections.
We only recommend applying the contact diary method either when the planned analyses are robust against the expected reporting errors and biases, or when the relevant contacts are so intense that the expected level of reporting accuracy is sufficient. When possible, diary-based approaches should be complemented with other approaches, like measurements made with wearable sensor badges that precisely record close spatial co-location [Reference Salathé19–Reference Pentland21]. Such complementary measurements allow data cross-validation and provide more robust insights into a system's contact topology.
ACKNOWLEDGEMENTS
This research was funded by the Swiss National Science Foundation (project 32003B_127548). The cooperation and commitment of the 50 participants made this study possible. Mirjam Kretzschmar, Lena Fiebig, Corinne Moser, Andrea Ulrich, Anna Drewek, and Jan Hattendorf helped to improve the quality of this paper with their valuable comments. We thank two anonymous referees for their thorough review of our manuscript that further advanced our work. Sandro Bösch helped with the final layout of the figures. The manuscript was copyedited by EditMyEnglish.
NOTE
Supplementary material accompanies this paper on the Journal's website (http://journals.cambridge.org/hyg).
DECLARATION OF INTEREST
None.






