Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T02:51:10.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Cost-effectiveness analysis of a hypothetical hepatitis C vaccine compared to antiviral therapy

Published online by Cambridge University Press:  17 July 2008

E. MASSAD ,
F. A. B. COUTINHO ,
E. CHAIB  and
M. N. BURATTINI
E. MASSAD
Affiliation:
School of Medicine, University of São Paulo, Brazil LIM01 – HCFMUSP, São Paulo, Brazil London School of Hygiene and Tropical Medicine, London, UK
F. A. B. COUTINHO
Affiliation:
School of Medicine, University of São Paulo, Brazil LIM01 – HCFMUSP, São Paulo, Brazil
E. CHAIB
Affiliation:
LIM01 – HCFMUSP, São Paulo, Brazil Oxford University, Oxford, UK
M. N. BURATTINI*
Affiliation:
School of Medicine, University of São Paulo, Brazil LIM01 – HCFMUSP, São Paulo, Brazil
*
*Author for correspondence: Dr M. N. Burattini, School of Medicine, University of São Paulo, Av. Dr. Arnaldo 455, São Paulo, CEP 01246-903, 7382, SP, Brazil. (Email: mnburatt@usp.br)
Rights & Permissions [Opens in a new window]

Summary

We propose a mathematical model to simulate the dynamics of hepatitis C virus (HCV) infection in the state of São Paulo, Brazil. We assumed that a hypothetical vaccine, which cost was taken to be the initial cost of the vaccine against hepatitis B exists and it is introduced in the model. We computed its cost-effectiveness compared with the anti-HCV therapy. The calculated basic reproduction number was 1·20. The model predicts that without intervention a steady state exists with an HCV prevalence of 3%, in agreement with the current epidemiological data. Starting from this steady state three interventions were simulated: indiscriminate vaccination, selective vaccination and anti-HCV therapy. Selective vaccination proved to be the strategy with the best cost-effectiveness ratio, followed by indiscriminate vaccination and anti-HCV therapy.

Keywords

Basic reproduction numbercost-effectiveness analysishepatitis Cmodellingvaccination
Type
Original Papers
Information
Epidemiology & Infection , Volume 137 , Issue 2 , February 2009 , pp. 241 - 249
Copyright
Copyright © 2008 Cambridge University Press

INTRODUCTION

The hepatitis C virus (HCV) was first identified in 1988, although its existence had been suspected for some time [Reference Crofts, Thompson and Kaldor1]. It is a non-cytopathic hepatotropic member of the Flaviridae family that causes acute and chronic hepatitis, and hepatocellular carcinoma (HCC) [Reference Hoofnagle2]. It infects about 170 million people worldwide [3–Reference Poynard5], being particularly prevalent among high-risk populations, such as intravenous illicit drug users and inmates of correctional institutions [Reference Strazza6, Reference Burattini7]. In untreated patients, the median expected time to cirrhosis is 30 years; 33% of patients have an expected median time to cirrhosis of <20 years and 31% will only progress to cirrhosis after >50 years, if ever [Reference Poynard5]. There is no vaccine, and the available antiviral drugs are toxic, expensive and only partly effective [Reference Chisari8]. The combination of pegylated interferon-α with ribavirin, the latest treatment for HCV infection, elicits long-term responses in only 50% of the patients [9]. However, a vaccine might be within reach [Reference Hoofnagle2]. Chimpanzees that are challenged after clearance of primary HCV infection are protected against homologous and heterologous viral isolates [Reference Basset10]. This has generated optimism about the development of at least a partly effective vaccine against HCV [Reference Houghton and Abignoni11].

Hepatitis C is the most common indication for orthotropic liver transplantation, accounting for about 50% of individuals on the waiting list [Reference Brown12]. Liver transplantation has altered the natural history of end-stage liver disease and is now considered the preferred therapy for a wide range of previously fatal chronic hepatic diseases [Reference Merion13], including HCV-related liver failure. However, the number of people transplanted each year is much lower than the number of people that are on the waiting list and thousands of patients die every year while on waiting lists [Reference Chaib and Massad14].

In this paper we propose a mathematical model of the transmission dynamics of HCV in the state of São Paulo, Brazil, which allows the analysis of the impact of a hypothetical vaccine compared to the traditional antiviral treatment on several indicators of liver failure that evolve to liver transplantation. Although it is expected that an efficient vaccine will reduce the number of liver failure cases, it is not known whether it is more or less cost-effective than the antiviral treatment. The estimation of the cost-effectiveness of both the vaccine and the antiviral treatment is complicated by the fact that there are other causes of liver failure and transplant indication than HCV, accounting for about 50% of the total liver transplantations. Therefore a model is required to estimate the impact of a vaccine – with variable intensity of application and cost vis-à-vis a treatment whose efficiency and cost is also variable.

The model

The model assumes a population divided into 22 states. Susceptible individuals, denoted S(t), are subdivided into two classes, denoted S 1(t) representing the general population and S 2(t), representing a group with higher risk of acquiring the infection by HCV, like injecting drug users, recipients of blood/blood products, transfusion, people occupationally exposed to blood/blood products, etc. S 1(t) individuals are transferred to the high-risk group S 2(t) with rate ξ. Both susceptible classes acquire the infection with rates βi (i=1, …, 4) from four different types of individuals, namely, infected and asymptomatic but already infectious individuals, denoted HCV +(t), individuals with acute hepatitis, denoted Ac(t), individuals with acute hepatitis and treated, denoted T A(t), and individuals with intermediate fibrosis stages, called ‘chronic state’, denoted Chr(t). Only a fraction u of βi is effective for people in the non-risk group. Susceptible individuals can also be vaccinated with a hypothetical vaccine at rate ν, which has efficacy f and duration ψi−1(i=1, 2), after which they are seen as vaccinated, denoted by Vac(t). In addition, susceptible individuals can develop other hepatopathies causing liver failure with rate ω, after which they are transferred to the state designated Oth(t). Infected and asymptomatic individuals, HCV +(t), can evolve to acute or chronic hepatitis, with rates σ1 and σ2 respectively. A proportion p of individuals with acute hepatitis, Ac(t), can be treated and are then transferred to the treated compartment, T A(t), with rate pδ1. The non-treated individuals evolve to Chr(t), at rate (1−p)δ1. Treated individuals, in turn, can also evolve to the chronic state at rate σ3. Once in the chronic state individuals can either evolve to hepatocellular carcinoma, denoted HCC(t), at rate θ, or evolve to liver failure at rate δ2. We consider only four levels [Reference Crofts, Thompson and Kaldor1] of the Model for End-stage Liver Disease (MELD), a scale of hepatopathy that incorporates three widely available laboratory variables including the international normalized ratio (INR), serum creatinine, and serum bilirubin [Reference Brown12]. In addition, a proportion q of chronic individuals can be treated [Reference Brown12]. Those treated individuals with liver failure are denoted T CM i (i=1, …, 4), and those untreated are denoted NT CM i (i=1, …, 4). Evolution between the MELD levels occurs at rates εi (i=1, …, 6). Infected individuals and those treated can recover to compartment R at rates γi (i=1, …, 8). Individuals from compartments T CM i (i=1, …, 4), NT CM i (i=1, …, 4), and HCC get onto the waiting list for liver transplantation, WL(t), at rates ϕi (i=1, …, 9) and Oth with rate λ. Individuals on the waiting list are eventually transplanted at rate τ1. We also consider the possibility of loss of graft at rate ϕ10, and a secondary waiting list WLTx. From the latter, individuals are eventually transplanted at rate τ2. Every individual in this population is subjected to a mortality rate μ and an additional mortality of those with liver disease occurs at rates αi (i=1, …, 16) depending on the state. Finally, the susceptible compartment grows at rate Λ, which comprises by the sum of all mortalities in order to keep the total population constant.

The model's dynamics are described by the following set of equations:

\hskip-1\eqalign{ {d \over {{\rm d}t}}S_{\setnum{1}} \lpar t\rpar \equals \tab \rmLambda\hskip-1 \minus u\beta _{\setnum{1}} HCV\lpar t\rpar {{S_{\setnum{1}} \lpar t\rpar } \over N} \hskip-2\minus u\beta _{\setnum{2}} Ac\lpar t\rpar {{S_{\setnum{1}} \lpar t\rpar } \over N} \hskip-2\minus u\beta _{\setnum{3}} T_{A} \lpar t\rpar {{S_{\setnum{1}} \lpar t\rpar } \over N} \hskip-2 \minus u\beta _{\setnum{4}} Chr\lpar t\rpar {{S_{\setnum{1}} \lpar t\rpar } \over N} \hskip-2\minus \lpar fv_{\setnum{1}} \plus \mu \plus \omega \plus \xi \rpar S_{\setnum{1}} \lpar t\rpar \plus \psi _{\setnum{1}} Vac\lpar t\rpar \cr}
\eqalign{ {d \over {{\rm d}t}}S_{\setnum{2}} \lpar t\rpar \equals \tab \xi S_{\setnum{1}} \lpar t\rpar \minus \beta _{\setnum{1}} HCV\lpar t\rpar {{S_{\setnum{2}} \lpar t\rpar } \over N} \minus \beta _{\setnum{2}} Ac\lpar t\rpar {{S_{\setnum{2}} \lpar t\rpar } \over N} \minus \beta _{\setnum{3}} T_{A} \lpar t\rpar {{S_{\setnum{2}} \lpar t\rpar } \over N} \minus \beta _{\setnum{4}} Chr\lpar t\rpar {{S_{\setnum{2}} \lpar t\rpar } \over N} \minus \lpar fv_{\setnum{2}} \plus \mu \plus \omega \rpar S_{\setnum{2}} \lpar t\rpar \plus \psi _{\setnum{2}} Vac\lpar t\rpar \cr}
\eqalign{ {d \over {{\rm d}t}}HCV^{ \plus } \lpar t\rpar \equals \tab \beta _{\setnum{1}} HCV^{ \plus } \lpar t\rpar {{\lpar uS_{\setnum{1}} \lpar t\rpar \plus S_{\setnum{2}} \lpar t\rpar \rpar } \over N} \plus \beta _{\setnum{2}} Ac\lpar t\rpar {{\lpar uS_{\setnum{1}} \lpar t\rpar \plus S_{\setnum{2}} \lpar t\rpar \rpar } \over N} \plus \beta _{\setnum{3}} T_{A} \lpar t\rpar {{\lpar uS_{\setnum{1}} \lpar t\rpar \plus S_{\setnum{2}} \lpar t\rpar \rpar } \over N}\cr \tab \plus \beta _{\setnum{4}} Chr\lpar t\rpar {{\lpar uS_{\setnum{1}} \lpar t\rpar \plus S_{\setnum{2}} \lpar t\rpar \rpar } \over N} \minus \lpar \gamma _{\setnum{1}} \plus \sigma _{\setnum{1}} \plus \sigma _{\setnum{2}} \plus \mu \rpar HCV^{ \plus } \lpar t\rpar \cr}
{d \over {{\rm d}t}}Ac\lpar t\rpar \equals \sigma _{\setnum{1}} HCV^{ \plus } \lpar t\rpar \minus \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \alpha _{\setnum{1}} \plus \mu \rpar Ac\lpar t\rpar
{d \over {{\rm d}t}}T_{A} \lpar t\rpar \equals p\delta _{\setnum{1}} Ac\lpar t\rpar \minus \lpar \gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \alpha _{\setnum{2}} \plus \mu \rpar T_{A} \lpar t\rpar
\eqalign{ {d \over {{\rm d}t}}R\lpar t\rpar \equals \tab \gamma _{\setnum{1}} HCV^{ \plus } \lpar t\rpar \plus \gamma _{\setnum{2}} Ac\lpar t\rpar \plus \gamma _{\setnum{3}} T_{A} \lpar t\rpar \plus \gamma _{\setnum{4}} T_{C} M_{\setnum{1}} \lpar t\rpar \plus \gamma _{\setnum{5}} T_{C} M_{\setnum{2}} \lpar t\rpar \plus \gamma _{\setnum{6}} T_{C} M_{\setnum{3}} \lpar t\rpar \plus \gamma _{\setnum{7}} T_{C} M_{\setnum{4}} \lpar t\rpar \cr \tab\plus \lpar q\delta _{\setnum{5}} \plus \gamma _{\setnum{8}} \rpar Chr\lpar t\rpar \minus \mu R\lpar t\rpar \cr}
{d \over {{\rm d}t}}Vac\lpar t\rpar \equals fv_{\setnum{1}} S_{\setnum{1}} \lpar t\rpar \plus fv_{\setnum{2}} S_{\setnum{2}} \lpar t\rpar \minus \lpar \mu \plus \omega \plus \psi _{\setnum{1}} \plus \psi _{\setnum{2}} \rpar Vac\lpar t\rpar
\eqalign{ {d \over {{\rm d}t}}Chr\lpar t\rpar \equals \tab \lpar 1 \minus p\rpar \delta _{\setnum{2}} Ac\lpar t\rpar \plus \sigma _{\setnum{2}} HCV^{ \plus } \plus \sigma _{\setnum{3}} T_{A} \minus \lpar q\delta _{\setnum{3}} \plus \lpar 1 \minus q\rpar \delta _{\setnum{4}} \plus q\delta _{\setnum{5}} \plus \theta \plus \alpha _{\setnum{3}} \plus \gamma _{\setnum{8}} \rpar Chr\lpar t\rpar \cr}
{d \over {{\rm d}t}}T_{C} M_{\setnum{1}} \lpar t\rpar \equals q\delta _{\setnum{3}} Chr\lpar t\rpar \minus \lpar \gamma _{\setnum{4}} \plus \phiv _{\setnum{1}} \plus \epsiv _{\setnum{1}} \plus \alpha _{\setnum{5}} \plus \mu \rpar T_{C} M_{\setnum{1}} \lpar t\rpar
{d \over {{\rm d}t}}T_{C} M_{\setnum{2}} \lpar t\rpar \equals \epsiv _{\setnum{1}} T_{C} M_{\setnum{1}} \lpar t\rpar \minus \lpar \gamma _{\setnum{5}} \plus \phiv _{\setnum{2}} \plus \epsiv _{\setnum{2}} \plus \alpha _{\setnum{6}} \plus \mu \rpar T_{C} M_{\setnum{2}} \lpar t\rpar
{d \over {{\rm d}t}}T_{C} M_{\setnum{3}} \lpar t\rpar \equals \epsiv _{\setnum{2}} T_{C} M_{\setnum{2}} \lpar t\rpar \minus \lpar \gamma _{\setnum{6}} \plus \phiv _{\setnum{3}} \plus \epsiv _{\setnum{3}} \plus \alpha _{\setnum{7}} \plus \mu \rpar T_{C} M_{\setnum{3}} \lpar t\rpar
{d \over {{\rm d}t}}T_{C} M_{\setnum{4}} \lpar t\rpar \equals \epsiv _{\setnum{3}} T_{C} M_{\setnum{3}} \lpar t\rpar \minus \lpar \gamma _{\setnum{7}} \plus \phiv _{\setnum{4}} \plus \alpha _{\setnum{8}} \plus \mu \rpar T_{C} M_{\setnum{4}} \lpar t\rpar
{d \over {{\rm d}t}}NT_{C} M_{\setnum{1}} \lpar t\rpar \equals \lpar 1 \minus q\rpar \delta _{\setnum{4}} Chr\lpar t\rpar \minus \lpar \phiv _{\setnum{5}} \plus \epsiv _{\setnum{4}} \plus \alpha _{\setnum{9}} \plus \mu \rpar NT_{C} M_{\setnum{1}} \lpar t\rpar
{d \over {{\rm d}t}}NT_{C} M_{\setnum{2}} \lpar t\rpar \equals \epsiv _{\setnum{4}} NT_{C} M_{\setnum{1}} \lpar t\rpar \minus \lpar \phiv _{\setnum{6}} \plus \epsiv _{\setnum{5}} \plus \alpha _{\setnum{10}} \plus \mu \rpar NT_{C} M_{\setnum{2}} \lpar t\rpar
{d \over {{\rm d}t}}NT_{C} M_{\setnum{3}} \lpar t\rpar \equals \epsiv _{\setnum{5}} NT_{C} M_{\setnum{2}} \lpar t\rpar \minus \lpar \phiv _{\setnum{7}} \plus \epsiv _{\setnum{6}} \plus \alpha _{\setnum{11}} \plus \mu \rpar NT_{C} M_{\setnum{3}} \lpar t\rpar
{d \over {{\rm d}t}}NT_{C} M_{\setnum{4}} \lpar t\rpar \equals \epsiv _{\setnum{6}} NT_{C} M_{\setnum{3}} \lpar t\rpar \minus \lpar \phiv _{\setnum{8}} \plus \alpha _{\setnum{12}} \plus \mu \rpar NT_{C} M_{\setnum{4}} \lpar t\rpar
{d \over {{\rm d}t}}HCC\lpar t\rpar \equals \theta Chr\lpar t\rpar \minus \lpar \phiv _{\setnum{9}} \plus \alpha _{\setnum{4}} \plus \mu \rpar HCC\lpar t\rpar
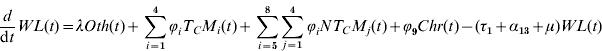
\eqalign{ {d \over {{\rm d}t}}WL\lpar t\rpar \equals \tab \lambda Oth\lpar t\rpar \plus \sum\limits_{i \equals \setnum{1}}^{\setnum{4}} {\phiv _{i} T_{C} M_{i} \lpar t\rpar \plus \sum\limits_{i \equals \setnum{5}}^{\setnum{8}} {\sum\limits_{j \equals \setnum{1}}^{\setnum{4}} {\phiv _{i} NT_{C} M_{j} \lpar t\rpar } } } \plus \phiv _{\setnum{9}} Chr\lpar t\rpar \minus \lpar \tau _{\setnum{1}} \plus \alpha _{\setnum{13}} \plus \mu \rpar WL\lpar t\rpar \cr}
{d \over {{\rm d}t}}Tx_{\setnum{1}} \lpar t\rpar \equals \tau _{\setnum{1}} WL\lpar t\rpar \minus \lpar \phiv _{\setnum{10}} \plus \alpha _{\setnum{14}} \plus \mu \rpar Tx_{\setnum{1}} \lpar t\rpar
{d \over {{\rm d}t}}WLTx\lpar t\rpar \equals \phiv _{\setnum{10}} Tx_{\setnum{1}} \lpar t\rpar \minus \lpar \tau _{\setnum{2}} \plus \alpha _{\setnum{15}} \plus \mu \rpar WLTx\lpar t\rpar
{d \over {{\rm d}t}}Tx_{\setnum{2}} \lpar t\rpar \equals \tau _{\setnum{2}} WLTx\lpar t\rpar \minus \lpar \alpha _{\setnum{16}} \plus \mu \rpar Tx_{\setnum{2}} \lpar t\rpar
(1)
{d \over {{\rm d}t}}Oth\lpar t\rpar \equals \omega \lpar S\lpar t\rpar \plus Vac\lpar t\rpar \rpar \minus \lpar \lambda \plus \alpha _{\setnum{17}} \plus \mu \rpar Oth\lpar t\rpar .

The biological meaning, the values of the parameters and their sources can be seen in Table 1.

Table 1. Parameters used in the simulations

MELD, Model for End-stage Liver Disease.

The basic reproduction number

To calculate the system's basic reproductive number we used the method described in Lopez et al. [Reference Lopez15]. The method consists of linearizing system (1) around the trivial solution, i.e. in the absence of infection, and analyses the real part of the linearized system matrix's eigenvalues.

It is sufficient to consider only the compartments that effectively contribute to the spread of the infection, namely the asymptomatic seropositives, HCV +, the individuals with acute hepatitis, A, individuals with acute hepatitis but under treatment, T A, and individuals with chronic hepatitis, Chr.

The linearized system (1) has the following form:

(2)
\openup3\matrix{ {{\displaystyle{d \over {{\rm d}t}}}HCV^{ \plus } \lpar t\rpar } \hfill \tab \equals \hfill \tab {\left( \beta _{\setnum{1}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right) \minus \gamma _{\setnum{1}} \minus \sigma _{\setnum{1}} \minus \sigma _{\setnum{2}} \minus \mu \right) HCV^{ \plus } \lpar t\rpar \plus \beta _{\setnum{2}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)Ac\lpar t\rpar } \hfill \cr {} \hfill \tab {} \hfill \tab \plus{\beta _{\setnum{3}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)T_{A} \lpar t\rpar \plus \beta _{\setnum{4}} \left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)Chr\lpar t\rpar } \hfill \cr {{\displaystyle{d \over {{\rm d}t}}}Ac\lpar t\rpar } \hfill \tab \equals \hfill \tab {\sigma _{\setnum{1}} HCV^{ \plus } \lpar t\rpar \minus \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \mu \plus \alpha _{\setnum{1}} \rpar Ac\lpar t\rpar } \hfill \cr {{\displaystyle{d \over {{\rm d}t}}}T_{A} \lpar t\rpar } \hfill \tab \equals \hfill \tab {p\delta _{\setnum{1}} Ac\lpar t\rpar \minus \lpar \gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \mu \plus \alpha _{\setnum{2}} \rpar T_{A} \lpar t\rpar } \hfill \cr {{\displaystyle{d \over {{\rm d}t}}}Chr\lpar t\rpar } \hfill \tab \equals \hfill \tab {\sigma _{\setnum{2}} HCV^{ \plus } \lpar t\rpar \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} Ac\lpar t\rpar \plus \sigma _{\setnum{3}} T_{A} \lpar t\rpar \minus } \hfill {\lpar q\lpar \delta _{\setnum{3}} \plus \delta _{\setnum{5}} \rpar \plus \lpar 1 \minus q\rpar \delta _{\setnum{4}} \plus \theta \plus \mu \plus \alpha _{\setnum{3}} \plus \gamma _{\setnum{8}} \rpar Chr\lpar t\rpar } .\hfill \cr}

The basic reproductive number, calculated according to the method described previously [Reference Lopez15] results in:

(3)
\openup3\eqalign { R_{\setnum{0}} \equals\hskip1\tab {{{\beta _{\setnum{1}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)} \over {\lpar \gamma _{\setnum{1}} \plus \sigma _{\setnum{1}} \plus \sigma _{\setnum{2}} \plus \mu \rpar }}} \plus {{{\beta _{\setnum{2}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)\sigma _{\setnum{1}} } \over {\lpar \gamma _{\setnum{1}} \plus \sigma _{\setnum{1}} \plus \sigma _{\setnum{2}} \plus \mu \rpar \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \mu \plus \alpha _{\setnum{1}} \rpar }}} \cr \tab \plus {{{\beta _{\setnum{3}}\displaystyle \left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)p\delta _{\setnum{1}} \sigma _{\setnum{2}} } \over {\lpar \gamma _{\setnum{1}} \plus \sigma _{\setnum{1}} \plus \sigma _{\setnum{2}} \plus \mu \rpar \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \mu \plus \alpha _{\setnum{1}} \rpar \lpar \gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \alpha _{\setnum{2}} \plus \mu \rpar }}} \cr \tab \plus {{{\beta _{\setnum{4}} \displaystyle\left( {{{uS_{\setnum{1}} \lpar 0\rpar \plus S_{\setnum{2}} \lpar 0\rpar } \over N}} \right)[\phantom{N\over\N}\hskip-8 {\left( {\gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \alpha _{\setnum{2}} \plus \mu } \right)\,\delta _{\setnum{2}} \sigma _{\setnum{1}} \lpar 1 \minus p\rpar \plus p\sigma _{\setnum{1}} \sigma _{\setnum{3}} \delta _{\setnum{1}} \plus \lpar \gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \alpha _{\setnum{2}} \plus \mu \rpar \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \mu \plus \alpha _{\setnum{1}} \rpar \sigma _{\setnum{2}} } ]} \over {\lpar \gamma _{\setnum{1}} \plus \sigma _{\setnum{1}} \plus \sigma _{\setnum{2}} \plus \mu \rpar \lpar p\delta _{\setnum{1}} \plus \lpar 1 \minus p\rpar \delta _{\setnum{2}} \plus \gamma _{\setnum{2}} \plus \mu \plus \alpha _{\setnum{1}} \rpar \lpar \gamma _{\setnum{3}} \plus \sigma _{\setnum{3}} \plus \alpha _{\setnum{2}} \plus \mu \rpar \lpar q\lpar \delta _{\setnum{3}} \plus \delta _{\setnum{5}} \rpar \plus \lpar 1 \minus q\rpar \delta _{\setnum{4}} \plus \theta \plus \mu \plus \alpha _{\setnum{3}} \plus \gamma _{\setnum{8}} \rpar }}\vskip-1 .} \cr}

Simulating the model

Using the Latin Hypercube Sampling (LHCS) procedure [Reference Luz16], which is an extremely efficient sampling design proposed by McKay et al. [Reference McKay, Beckman and Conover17], values for the parameters were generated. The parameters used in the simulation can be seen in Table 1, and their values were chosen with the LHCS technique in order to reproduce the real endemic situation in the state of São Paulo, Brazil with reasonable accuracy, e.g. HCV prevalence of 3% [3, Reference Chaib and Massad14], the number of transplantations, the size of the waiting list and the number of people that die while on the waiting list (described in [Reference Chaib and Massad14]). Therefore, comparing the model's outcome with Table 1 from [Reference Chaib and Massad14] we see that, for 2004 the number of liver transplantations predicted by the model was 265, against the observed 295; the incidence of new patients on the waiting list was predicted as 1544 against the observed 1500; and the number of deaths on the waiting list predicted by the model was 673 against the observed 671. The combination of the parameters described in Table 1, applied to equation (3) resulted in a basic reproduction number of 1·20 (95% CI 1·18–1·23). With such a low basic reproduction number, we expect that removing susceptibles by vaccination will be very efficient in controlling the disease. As described below, we examined two vaccination strategies, indiscriminate and selective. In addition, we simulate four types of vaccine, namely a vaccine with 100% efficacy and lifelong protection, a vaccine with 100% efficacy and 10 years of protection, a vaccine with 80% efficacy and lifelong protection, and a vaccine with 80% efficacy and 10 years of protection.

The model predicts that without intervention the disease will evolve to a steady state, reaching a HCV infection prevalence of 3%. Starting from this system in steady state we simulated the result of an anti-HCV therapy applied to all HCV-infected individuals and analysed the maximum reduction in the disease prevalence after 20 years of simulation. This was set as a standard to be compared with the vaccination rates used. We therefore analysed the vaccination rates that would reduce the disease prevalence by the same amount in 20 years of therapy. The two vaccination strategies are ‘indiscriminate’ vaccination that would cover both the non-risk and risk groups, S 1(t) and S 2(t), and one called ‘selective’ vaccination that would cover only the risk group, S 2(t). Next, we computed the results of 20 years of intervention: the final prevalence; the number of individuals treated or vaccinated; the costs involved in each control strategy; the number of averted disease; the cost per averted disease; the number of averted deaths; and the cost per averted death. Individual cost per vaccination was set at US$300 (assumed similar to the initial anti-HBV vaccine costs). Based on clinical trial data, 48 weeks of pegylated-interferon/ribavirin combination therapy should cost about US$8000, which includes the cost of the drugs, management of adverse events, and estimates of health-care resource utilization including office visits, laboratory tests, and contraception [Reference Wong18]. Cost analysis is presented in US$ due to this currency's role as an international reference currency. The results are summarized in Table 2.

Table 2. Results of the simulations (values in parentheses are 95% confidence intervals)

Vacine strategy 1: Lifelong immunity, 100% efficacy, indiscriminate vaccination.

Vacine strategy 2: Lifelong immunity, 100% efficacy, selective vaccination.

Vacine strategy 3: 10 year-long immunity, 100% efficacy, indiscriminate vaccination.

Vacine strategy 4: 10 year-long immunity, 100% efficacy, selective vaccination.

Vacine strategy 5: Lifelong immunity, 80% efficacy, indiscriminate vaccination.

Vacine strategy 6: Lifelong immunity, 80% efficacy, selective vaccination.

Vacine strategy 7: 10 year-long immunity, 80% efficacy, indiscriminate vaccination.

Vacine strategy 8: 10 year-long immunity, 80% efficacy, selective vaccination.

From Table 2 it can be seen that the total costs of the different vaccination strategies considered that resulted in the same reduction in hepatitis C prevalence varies from about half to five times that of antiviral therapy. The number of individuals treated or vaccinated, varied from around 330 000 to 34 000 000, again depending on the vaccination strategy considered. The number of averted disease with vaccination is always greater (from 2–4 times) than that of antiviral therapy, being maximized by strategy 2 (100% efficacy vaccine, with lifelong protection and selective indication). As for the number of averted deaths, antiviral therapy is the strategy that maximizes it in the period of 20 years of intervention. Finally, strategy 2 is the one that minimizes both the costs of averted disease and averted deaths (see Figs 1 and 2).

Fig. 1. Cost per averted disease in US$ for the antiviral treatment compared with the eight vaccination strategies simulated. The meaning of each vaccination strategy is the same as in Table 2. T, Treatment.

Fig. 2. Cost per averted death in US$ for the antiviral treatment compared with the eight vaccination strategies simulated. The meaning of each vaccination strategy is the same as in Table 2. T, Treatment.

From Table 2 and Figures 1 and 2 it can also be noted that selective vaccination is always more effective than indiscriminate vaccination. In addition, when analysing the costs per averted disease we can see that all selective vaccination strategies along with strategies 1 and 5 (indiscriminate vaccination with lifelong protection, 100% or 80% efficient) are better than the competing antiviral therapy strategy. However, when considering the cost per averted deaths, only the selective vaccination strategies with lifelong immunity (strategies 2 and 6) are better than antiviral therapy.

CONCLUSIONS

In this work we present an original model for HCV transmission and applied it in the state of São Paulo, Brazil, to analyse the impact of a hypothetical vaccine against HCV on the proportion of averted disease and deaths, and on the cost-effectiveness ratio compared to antiviral treatment. We did this motivated by the importance of HCV in public health, since it afflicts almost 200 million people worldwide, costing millions of dollars and a huge number of human lives [3–Reference Poynard5], and also by the probable development of an effective vaccine [Reference Houghton and Abignoni11]. It is not yet clear whether a vaccine will be more or less efficient in reducing disease and deaths due to hepatitis C and if it will be more or less cost-effective than the antiviral anti-HCV therapy. The proposed model was designed to shed some light on these questions. In spite of its limitations related to the uncertainty in the parameter values, the model demonstrated a number of interesting features and reproduced the available epidemiological data of a given community. Although designed to fit the endemic situation of the state of São Paulo, Brazil, we believe that our model can be applied to other communities, provided that the necessary parameters are estimated with reasonable accuracy. It should also be noted that the found prevalence of hepatitis C of around 3% coincides with the accepted value for a global average. In addition, the basic reproduction number for the state of São Paulo is of the same order of magnitude of other studies, as mentioned below.

The estimated value of the basic reproduction number of 1·2 seems to be low for a disease with such large numbers of infected people. However, it is comparable to published values. For example, Pybus et al. [Reference Pybus19] found a value that ranged from 1·21 to 1·68. Schinaia [Reference Schinaia20] evaluated two scenarios: a high infectivity scenario where the basic reproduction number was estimated to be equal to 5·7, and a low infectivity scenario where this figure fell to around 1. Finally, Lloyd et al. [Reference Lloyd21] found the basic reproduction number to be 1·74.

We found that in the medium run (20 years) selective vaccination with 100% efficacy and lifelong immunity was the most cost-effective strategy. This conclusion is dependent on the estimated individual cost per vaccination and per anti-HCV therapy (US$300 and US$8000, respectively). Note, however, that US$300 is probably an overestimation of the expected vaccination cost, and therefore, our conclusion is the worst scenario for vaccination. Although selective vaccination poses enormous logistic difficulties (e.g. identifying who is actually at higher risk of acquisition of the infection), even some indiscriminate vaccination strategies were found to be more cost-effective than anti-HCV therapy.

DECLARATION OF INTEREST

None.

References

REFERENCES

1.Crofts, N, Thompson, S, Kaldor, J. Epidemiology of the hepatitis C virus. Technical Report Series No. 3, Communicable Diseases Network Australia and New Zealand, 1999.Google Scholar
2.Hoofnagle, JH. Course and outcome of hepatitis C. Hepatology 2002; 36: 521–559.Google Scholar
3.WHO. Hepatitis C global prevalence (updated). Weekly Epidemiological Record 2000; 75: 18–19.Google Scholar
4.Alter, HJ, Seeff, LB. Recovery, persistence and sequelae in hepatitis C virus infection: a perspective on long-term outcome. Seminars in Liver Diseases 2000; 20: 17–35.Google Scholar
5.Poynard, T, et al. Natural history of HCV infection. Bailliere's Clinical Gastroenterology 2000; 14: 211–228.Google Scholar
6.Strazza, L, et al. Behavior associated with HIV and HCV infection in female prison inmates in Sa~o Paulo, Brazil. Cadernos de Saude Publica 2007; 23: 197–205.Google Scholar
7.Burattini, MN, et al. Correlation between HIV and HCV in Brazilian prisoners: evidence for parenteral transmission inside prison. Revista de Saude Publica 2000; 34: 431–436.Google Scholar
8.Chisari, FV. Unscrambling hepatitis C virus-host interactions. Nature 2005: 436: 930–932.Google Scholar
9.National Institutes of Health. Consensus statement on management of hepatitis C. NIH Consensus Statement Records 2000; 75: 18–19.Google Scholar
10.Basset, SE, et al. Protective immune response to hepatitis C virus in chimpanzees rechallenged following clearance of primary infection. Hepatology 2001; 33: 1479–1487.Google Scholar
11.Houghton, M, Abignoni, S. Prospects for a vaccination against hepatitis C virus. Nature 2005; 436: 961–966.Google Scholar
12.Brown, RS Jr.. Hepatitis C and liver transplantation. Nature 2005; 436: 973–978.Google Scholar
13.Merion, RM, et al. The survival benefit of liver transplantation. American Journal of Transplantation 2005; 5: 307–313.Google Scholar
14.Chaib, E, Massad, E. Liver transplantation: waiting list dynamics in the State of São Paulo, Brazil. Transplantation Proceedings 2005; 37: 4329–4330.Google Scholar
15.Lopez, LF, et al. Threshold conditions for infection persistence in complex host-vectors interactions. Comptes Rendus Biologies 2002; 325: 1073–1084.Google Scholar
16.Luz, PM, et al. Uncertainties regarding dengue modeling in Rio de Janeiro, Brazil. Memórias do Instituto Oswaldo Cruz 2003; 98: 871–878.Google Scholar
17.McKay, MD, Beckman, RJ, Conover, WJ. A Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979; 21: 239–245.Google Scholar
18.Wong, JB. Hepatitis C: achieving maximum results putting combination therapy for HCV into practice. Digestive Disease Week. 1999 Annual Meeting (http://www.hepnet.com/hepc/DDW99/HCVSGP/wong.html). Accessed 5 October 2007.Google Scholar
19.Pybus, OG, et al. The epidemic behavior of the hapatitis C virus. Science 2001; 292: 2323–2325.Google Scholar
20.Schinaia, G. Empirical data and mathematical structures in the epidemic modeling of parenteral hepatitis in Italy. Advances in Complex Systems 2005; 8: 33–58.Google Scholar
21.Lloyd, AL. The dependence of viral parameter estimates on the assumed viral life cycle: limitations of studies of viral load data. Proceedings of the Royal Society of London, Series B 2001; 268: 847–854.Google Scholar
22.Saltelli, A, Chan, K, Scott, EM. Sensitivity Analysis: Gauging the Worth of Scientific Models. Chichester: John Wiley & Sons, 2000.Google Scholar
23.Silva, LC, Pinho, JRR. Hepatitis C. In: Gayotto, LCC, Alves, VAFeds. Liver and Biliary Tract Diseases. São Paulo: Atheneu, 2001, pp. 470–487.Google Scholar
24.Instituto Brasileiro de Geografia e Estatística (http://www.ibge.gov.br/home/estatistica/populacao/default_censo_2000.shtm). Accessed 31 March 2008.Google Scholar
25.Gayotto, LCC, Alves, VAF. Doenças do Fígado e Vias Biliares. São Paulo: Atheneu, 2001.Google Scholar
26.Chaib, E, Ribeiro, MAF Jr., Saad, WA. Hepatocellular Carcinoma. São Paulo: Atheneu, 2004.Google Scholar
27.Brown, R Jr.. Hepatitis C and liver transplantation. Nature 2005; 436: 973–978.CrossRefGoogle ScholarPubMed
Figure 0

Table 1. Parameters used in the simulations

Figure 1

Table 2. Results of the simulations (values in parentheses are 95% confidence intervals)

Figure 2

Fig. 1. Cost per averted disease in US$ for the antiviral treatment compared with the eight vaccination strategies simulated. The meaning of each vaccination strategy is the same as in Table 2. T, Treatment.

Figure 3

Fig. 2. Cost per averted death in US$ for the antiviral treatment compared with the eight vaccination strategies simulated. The meaning of each vaccination strategy is the same as in Table 2. T, Treatment.