A hierarchical model for real-time monitoring of variation in risk of non-specific gastrointestinal infections

Summary

The AEGISS (Ascertainment and Enhancement of Disease Surveillance and Statistics) project uses spatio-temporal statistical methods to identify anomalies in the incidence of gastrointestinal infections in the UK. The focus of this paper is the modelling of temporal variation in incidence using data from the Southampton area in southern England. We identified and fitted a hierarchical stochastic model for the time series of daily incident cases to enable probabilistic prediction of temporal variation in risk, and demonstrated the resulting gains in predictive accuracy by comparison with a conventional analysis based on an over-dispersed Poisson log-linear regression model. We used Bayesian methods of inference in order to incorporate parameter uncertainty in our predictive inference of risk. Incorporation of our model in the overall spatio-temporal model, will contribute to the accurate and timely prediction of unusually high food-poisoning incidence, and thus to the identification and prevention of future outbreaks.

INTRODUCTION

Food poisoning is defined as ‘any disease of an infectious or toxic nature caused by the consumption of food or drink’ (Digestive Disorders Foundation, 2004). It is a common disease, with an estimated two million people infected each year in the UK. Reported cases usually present mild symptoms, typically including nausea, vomiting, abdominal cramps, headache and diarrhoea. Symptoms may extend to fever and chills, bloody stools, dehydration and nervous system damage. The severity of the infection is mostly determined by the species of the infectious agent; the most common bacteria responsible for food poisoning in the UK are Campylobacter and Salmonella. Although the illness is usually short-lived, it can be serious or even life-threatening, especially in vulnerable groups such as young children and the elderly.

Recording and investigating cases of suspected food poisoning can help the public health authorities to identify sources in order to prevent and control emerging outbreaks. However, current monitoring tools suffer from very incomplete reporting and delays in confirmation of reported cases. The AEGISS (Ascertainment and Enhancement of Disease Surveillance and Statistics) project was designed to address these deficiencies, with the aim of reducing the time of detection of a problem to 3 days (HPA press release, 12 February 2001). This would enable timely intervention in order to prevent further cases in the community. (For published work regarding the AEGISS project see [1–3].)

In this paper we present an extension of the work in Diggle et al. [2] which gave predictions of poor quality. This suggested that periodic review of the parameters of the fitted log-Gaussian Cox spatio-temporal process model [4] is required. Furthermore, it gave cause to doubt the adequacy of a static regression model for the continually changing temporal trend, thereby encouraging examination of stochastic models. We thus focus on modelling the underlying temporal variation of food-poisoning cases. Correct modelling of the time trend is essential for a correct interpretation of the spatio-temporal patterns in the data. If the mean number of daily incidences is overestimated or underestimated, the identification of spatially and temporally localized occurrences of unusually high incidence of food poisoning will be obscured. Time-series regression models for count data are the candidate stochastic models for the evolving temporal trend in incidence of food-poisoning cases. At a later stage, our model, incorporated in the overall spatio-temporal model presented in [2], will help in making valid predictions of food-poisoning cases towards the identification and prevention of future outbreaks.

METHODS

Data

Southampton was the test area and NHS Direct the source of the data used. NHS Direct is a 24-hour phone-in nurse advice and health information service, aimed at helping people in the UK to make the right choice and meeting their needs concerning medical issues. Information on NHS Direct is available at the service's website (www.nhsdirect.nhs.uk). The data gathered by NHS Direct are less likely to be incompatible and temporally restricted in reporting rates over time than the data provided by general practitioners (GPs). Moreover, they are more suitable for the predictive intentions of the AEGISS project, since the chance of reporting delays is eliminated, as no appointments are necessary.

The available data are the number of cases reported each day from August 2000 to December 2003. We discarded data prior to January 2001 because the service was new and not well established before that date. The service was out of use from 13 to 30 September 2001 inclusive, hence that part of the data was also removed. The proportion of zeros in the data for the 3 years 2001–2003 was 3%, i.e. on 32 out of the 1077 days there were no calls to NHS Direct. If the service was not in use on a particular day, for technical or other reasons, the number of cases was recorded as zero instead of as missing. We were therefore unable to distinguish between a fault in the NHS service resulting in no data, and no actual cases on those days.

In addition, food-poisoning incidence was different in 2001 compared to the corresponding daily incidence in the two subsequent years, with a lower mean and median and a larger proportion of zeros. Our aim was not to describe the mechanisms that lead to different behaviour at one point in time compared to another, but rather to find a suitable model with which to make valid predictions. Allowing the model to depend on unrepresentative data would result in inaccurate forecasts. Hence, we only considered data for 2002 and 2003, which are sufficiently well described by a Poisson distribution, the natural choice for distribution for count data. The 2001 data will be used later to assess the validity of our model.

Initial model fitting

We first fitted generalized linear models (GLMs [5]) to our data as an exploratory tool. There are standard and well established statistical tests to assess parameter significance and model fit for GLMs. Thus, using GLMs adjusted for over-dispersion [5], we examined the relationships between the daily number of food-poisoning cases with day-of-week effects and a linear time trend. Fourier terms up to the second harmonic were included in the model to account for seasonality in food-poisoning incidence. An assumed full model that adjusts for the effects of all the explanatory variables is

(1)

where δ_d(t) is the effect of the day-of-week and ω=2π/365 is the annual periodicity in incidence rates.

Hierarchical time-series models

The data exhibited temporal correlation and were hence not independently distributed as assumed for parametric (GLM) regression analysis. Our statistical model needed to account for the dependence between the observations. An inappropriate static model can be disastrous as it does not have the flexibility to adjust to model departures. A stochastic model would be expected to provide a better fit to our data and supply an improved forecasting tool.

The models we fitted to our data have the same justification as in [6] and were applied in a similar context, defining models for hierarchical analysis as in [7]. The hierarchy of the models was formulated in two levels:

1. (1) We assumed that conditionally on the means μ_t;t=1,…,T the observations y _t are independently distributed as Poisson random variables.

2. (2) The conditional means are related to the regression effects and the time-series random effects through the log-linear relationship

   (2)

   
   where X _t is the matrix of explanatory variables, β their regression coefficients (hence X _tβ=δ_d(t)+α₁ cos(ωt)+β₁ sin(ωt)+α₂ cos(2ωt)+β₂ sin(2ωt)+γt, as before), and W _t is an appropriately chosen stochastic process. W _t can be an autoregressive process of order suitably selected given the autocorrelations present in the data, a random noise process to account for extra variability in the data, or the sum of the two.

Bayesian Markov Chain Monte Carlo (MCMC) methods were used for inference. Their flexibility was exploited to fit a number of different models. MCMC methods provided posterior distributions for both regression and time-series parameters in our models and predictions were able to account for the uncertainty present in the parameter estimates.

Model comparisons

For each of the models fitted we calculated the deviance information criterion (DIC) and the mean square error prediction (MSEP) in order to identify the best-fitting model. DIC [8] is an asymptotic criterion that reflects both goodness of fit (i.e. residual variance) and degree of parameterization. It is defined as a classical estimate of fit, the deviance, plus twice the effective number of parameters, the complexity (the expected deviance minus deviance at the posterior expectation of the parameters), both calculated from MCMC output. Smaller DIC suggests a better model.

Our objective was to make future predictions based on the current data. Hence, the quality of predictions from each model should be assessed, and our choice of best-fitting model should reflect this. The MSEP criterion is usually the best measure of the quality of predictions and corresponds to predicting within the population from which the fitted data are drawn, as it represents the difference between the actual observations and the response predicted by the model.

Predictions

The AEGISS data are updated daily, and hence we were interested in short-term predictions because of the infectious nature of the disease. We calculated predictions for December 2003, the last month in the dataset used. These data were available, thus comparisons between predictions and the actual number of food-poisoning cases recorded were possible.

We first predicted the future values of the process W _t in our model, to discover how accurately we can predict the intensity of food-poisoning cases. Of the different kinds of predictions we were able to make using the {W _t} process, the most interesting were:

1. (1) Using data up to time t, make predictions for time point t+k. The same procedure was followed for different consecutive time points, t ₁, …, t _n. This is the so-called k-step-ahead predictor, which can be updated daily. For short-term predictions k is kept small. We used k=1 for one-step-ahead predictions.

2. (2) Using data up to the present time to predict the current intensity. This can be considered as the zero-step-ahead prediction in the previous category. This kind of prediction enables prediction of today's intensity and its evaluation as high or low compared with previous values. This predicted intensity can also be used to examine the spatial variation. Performing the same step on consecutive days would indicate whether the intensity remains at an elevated level, signalling outbreak, or returns to normal.

Finally, the question of whether our model can be used to make valid predictions of food-poisoning cases also arises. Making future forecasts involves simulation from the conditional distribution of daily incidence, conditional on the daily incidence up to time t (for details of all prediction types see the Supplementary Appendix, available online).

Software

We used WinBUGS, a recently developed software package [9] that implements the Gibbs sampler to fit time-series regression models using the Bayesian approach to our data. WinBUGS assumes a Bayesian model in which all parameters are treated as random variables. The posterior distribution of the parameters is obtained by conditioning on the data. The use of WinBUGS is justified by its flexibility and ease of use.

For validation of the Bayesian models fitted to the data, the results were processed in R, and the CODA package (convergence diagnosis and output analysis software for Gibbs sampling output) was used for analysing the output obtained from WinBUGS. R is an integrated suite of software facilities for data manipulation, calculation and graphical display (see http://www.r-project.org for details). CODA produces a number of plots: trace plots (to assess mixing of the chains), autocorrelation plots (high autocorrelations within chains indicate slow mixing and slow convergence), cross-correlation plots between the monitored variables for each chain (high correlations among parameters may result in slow convergence) and convergence diagnostics based on Cowles & Carlin [10].

RESULTS

Exploratory analysis

The data consisted of 6735 food-poisoning cases over the 2-year period 2002–2003, which yielded a daily mean number of 9·2 cases, and a variance of 18·8, suggesting the presence of over-dispersion [5].

It was expected that the daily incidence would be greater at weekends when the traditional sources of medical advice, such as GPs and nurse units, are unavailable [2]. The summary statistics of cases by day-of-week confirm this, since on Sundays the number of cases recorded is the highest and the number of cases recorded on Saturdays is relatively large compared to the corresponding number recorded on weekdays (Monday–Friday). We also include an ‘eighth weekday’ for public holidays (1, 2 January, 24, 25, 26 December and Good Friday). The average number of cases on a public holiday is larger than on normal weekends probably because GPs are often inaccessible on those days.

In Figure 1 the time-series plot over the years 2002–2003 suggests a seasonal pattern that peaks during the spring months. Additional smaller peaks appear during the autumns of 2002 and 2003. The sharpest increase in the number of cases was recorded during the period 21 December 2002 to 3 January 2003, indicating a possible outbreak during that period, which also includes 4 days classified as holidays. Figure 1 does not reveal any monotone (rising or decreasing) overall time trend.

Fig. 1. Time-series plot of gastrointestinal incidence in Southampton between 2002 and 2003.

Static model

The day-of-week effects were found to be strong and statistically significant, whereas the coefficients of the sinusoidal terms that account for and model the seasonal patterns in the data are only marginally significant. Under the incorrect assumption of independence between the observations made for a GLM model, the data can be interpreted as providing strong evidence of decreasing food-poisoning incidence.

The dependence between the observations can be assessed by the plots of the autocorrelation and partial autocorrelation functions. Using the raw data, the presence of serial correlation is obvious. The corresponding plots of the residuals of the GLM in Figure 2 are more instructive; any departure from white noise is identified by autocorrelation coefficients at any lag other than 1 lying outside these limits [11]. Serial dependence is no longer present. The 14th and 28th autocorrelation coefficients are now significant, which suggests that there might be correlation between the number of cases 2 or 4 weeks apart, implying a possible weekly effect. Biologically this cannot be justified, unless some variable that changes every 14 or 28 days and affects food-poisoning incidence, e.g. temperature, is not taken into account.

Fig. 2. Autocorrelation (left) and partial autocorrelation (right) functions of the Pearson residuals of the fitted generalized linear model. Dashed lines correspond to the 95% confidence intervals.

Time-series modelling

AR(1) model

The most commonly used time-series model is the autoregressive model of order 1 [7, 12, 13].

Here we assume that the observations are independently distributed as Poisson random variables. The conditional means are associated with the regression effects and the time-series random effects through

(3)

where A _t is an autoregressive process of order 1. Details on the analytical representation of the process and our choice for prior distributions are given in the Supplementary Appendix.

The posterior mean for the autoregressive parameter of the process (φ₁) is equal to 0·35, and the variance of the A _t values is ~0·08, which results in a rather rough autoregressive process. The autocorrelation plot of the residual process , where denotes the one-step-ahead forecast for y _t+1 made at time t, suggests that the process is consistent with the white-noise assumption and indicates a good model fit.

AR(2) model

We next replaced the autoregressive process of order 1 in the linear predictor of model (3) with an autoregressive process of order 2. This is identified as the trial over-fitting procedure [11], which states that, in general, in order to assess if the provisional time-series model is adequate, it should be compared with models that include an additional autoregressive parameter. The model with the higher-order process is preferred only if it provides improved model fit. Following the same fitting process as for the AR(1) model (see Supplementary Appendix), both the first- and second-order autoregressive parameters were found to be significant.

AR(7) model

The autocorrelation plots of the Pearson residuals of the GLM (Fig. 2) showed that at lags 14 and 28 the correlation coefficients are significant, possibly owing to an unaccounted temporal variable or a reporting effect. We thus defined an autoregressive process of order 7 (see Supplementary Appendix). The autoregressive parameters of the model were again found to be significant, but the residuals' process was not consistent with the white-noise assumption. This suggests that the added complexity induced by increasing the order of the autoregressive process is unnecessary.

Inclusion of extra random noise in the stochastic process

The considerable variability in our data induces a large variance in the time-series models presented. We thus added a random process {B _t}, to the linear predictors of each of the models AR(1), AR(2) and AR(7). This was intended to capture the variability of the data and reduce the roughness of the autoregressive process, leading to a smoother function of daily incidence over time, as desired. The second level of model (2) becomes

where B _t are independently and identically distributed Normal (0,τ²) variables.

The inclusion of the random-noise process resulted in a reduction in the variance of the autoregressive processes in the models by a factor of 20–25, suggesting that the random variation is absorbed in the random-noise process in all cases. In addition, the autoregressive parameters in the models are now larger; the biggest change being the change in the autoregressive parameter φ₁ from 0·35 in the AR(1) model to 0·91 when random noise is added. The increase in the autoregressive coefficients is an indication that by allowing for over-dispersion, the autoregressive processes becomes smoother and the strong dependence between observations is uncovered.

Model comparisons: final model

The values of DIC and MSEP for the stochastic models fitted are given in Table 1. Both criteria suggest that the best-fitting model is the one that includes an autoregressive process of order 1 {A _t}, and also incorporates extra random noise {B _t} in the stochastic process: y _t|μ_t ~ Poisson(μ_t)

(4)

Table 1. DIC and MSEP calculated for models 0–6

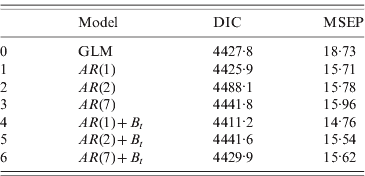
DIC, Deviance information criterion; MSEP, mean square error prediction; GLM, generalized linear model.

Models 1–3 correspond to autoregressive processes for orders 1, 2 and 7, respectively.

Models 4–6: same as models 1–3, plus random noise.

Table 2 summarizes the results for model (4). All parameters have much smaller variances than the those assigned to them a priori, suggesting that the prior distributions we chose were not influential and the outcomes reflect the patterns and associations present in the data. The strong and significant day-of-week effects dominate and the annual and 6-monthly cycles are not highly statistically significant (P<0·07). The autoregressive parameter (φ₁) is estimated as 0·91 with a small standard error, and the variance of the autoregressive process A _t is smaller than the variance of the random-noise process B _t, suggesting that the residual over-dispersion and the large variability in the data are captured by the random-noise process. Figure 3 shows the time-series plot of the number of cases. On the same plot, the random-noise process {B _t} (yellow line) as well as the smooth autoregressive {A _t} process (red line) are superimposed; both have been added to the mean daily incidence and exponentiated to be on the scale of the number of cases. The sinusoidal terms of the model were added to the A _t process, multiplied by their regression coefficients given in Table 2.

Fig. 3. Smooth function of daily incidence over time: raw data (- – -), posterior mean of (yellow line) and posterior mean of (red line).

Table 2. Final model

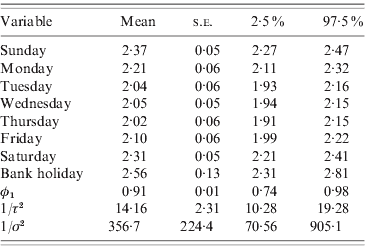
Mean, standard error (s.e.) and 95% credibility interval for all model parameters.

Predictions

Zero-step-ahead predictions of the {A_t} process

The zero-step ahead prediction is effectively the posterior mean of {A _t}, given data up to time t. We thus fit model (4) iteratively to datasets that have data for one additional day in each iteration. Figure 4 displays the posterior mean of the A _t values, t=700, …, 714, corresponding to 1–15 December 2003, given data up to time t (zero-step-ahead forecasts for A _t), their 95% credibility intervals, and the posterior means of the A _t values given the whole dataset (i.e. given data y ₁, …, y ₇₃₀). Since the autoregressive process is an unobserved latent process, we did not have the actual values of A _t to compare, so comparisons can only be made with the posterior means conditional on the whole dataset. We can infer that the two posterior means are quite close.

Fig. 4. Zero-step-ahead predictions for A _t, 1–15 December 2003: E(A _t|y ₁, …, y _t) (*), their 95% credibility intervals (+) and E(A _t|y ₁, …, y _t) (○).

One-step-ahead predictions of the {A_t} process

Figure 5 shows the posterior mean of A _t+1, t=700, …, 714 (1–15 December 2003), given data up to time t (one-step-ahead forecasts for A _t), their 95% credibility intervals and the posterior means of the A _t+1 values given the whole dataset (i.e. given data y ₁, …, y ₇₃₀). Comparing the two posterior means uncovers more randomness than in the procedure of calculating the zero-step-ahead predictions which leads to additional noise of the one-step-ahead predictions. However the predictions are still close to what we consider as the truth.

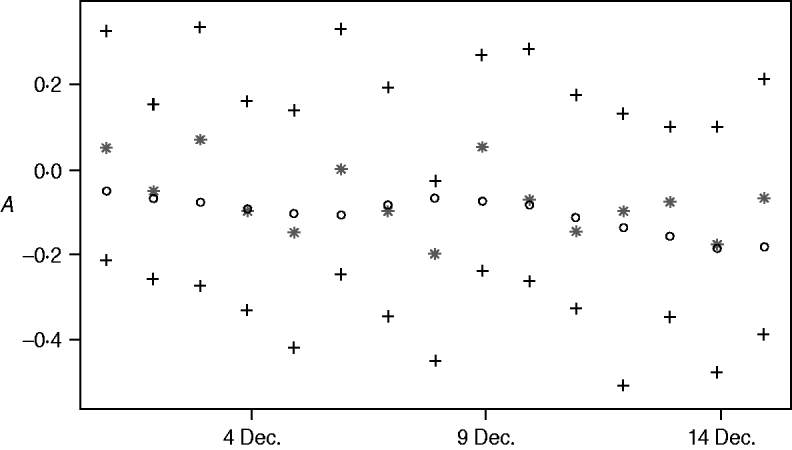
Fig. 5. One-step-ahead predictions for A _t, 1–15 December 2003: E(A _t+1|y ₁, …, y _t) (*), their 95% credibility intervals (+) and E(A _t+1|y ₁,…y _t) (○).

Future forecasts of daily number of food poisoning cases

Figure 6 presents the predictions and their 95% credibility interval superimposed on the actual number of food-poisoning cases in December 2003 (thus l=1, …, 31, t=699). The predictions appear to follow the pattern of the actual cases. The weekly cycles imposed by the model are roughly in accordance with the weekly cycles of the data. Only two observations fall out of the credibility intervals, which is to be expected for 31 observations and a 95% credibility interval.

Fig. 6. Predictions (•) and 95% credibility intervals (+) of food-poisoning cases in December 2003.

DISCUSSION

We have identified a model suitable for describing the food-poisoning dataset, that can be incorporated in the overall spatio-temporal model in [2]. The model allows for day-of-week effects and a seasonal pattern with high peaks in food-poisoning incidence in spring and lower peaks in autumn. It also allows for dependence between observations through a latent stochastic process which is adequately described by an autoregressive process of order 1, with small variance and high autoregressive parameter, showing evidence of a highly correlated underlying intensity. Empirical autocorrelations of the Poisson log-linear model, calculated before including the autoregressive process in our model, appeared to be small but still significant. Yet, those small autocorrelations are influential, as we may infer by the significance of the autoregressive parameter in our process. Their magnitude is masked by the residual over-dispersion in the model.

This over-dispersion is induced in the model by an unobserved spatio-temporal stochastic process [2], which is captured by the the random-noise process {B _t} in our model. Estimation of the underlying latent process is possible when taking into account the variation induced by the residual over-dispersion.

Our final model is robust since it is flexible and adapts quickly and effectively to changes in incidence. Furthermore, different types of predictions can be made using this model, each answering to a number of questions that may be of interest. The advantages of the proposed stochastic model over the temporal static model, that has been previously used to model the time-trend relationship of food-poisoning incidence, are its flexibility and its capability of giving adequate forecasts.

Overestimation or underestimation of the temporal variation in the incidence rate, which is the mean number of incident cases per day, would lead to overestimation or underestimation of the intensity of cases, which in turn would result in instances of high incidence being either masked or wrongly detected. A poor model for the temporal trend in the data would therefore result in poor information about food-poisoning cases being used by health professionals. On the other hand, a model that provides good fit to the data assists in meeting the AEGISS project's goals of quick and correct identification of outbreaks, which can be exploited to prevent their spread.

In summary, our suggested model can contribute to early detection of outbreaks of food poisoning when incorporated into the general spatio-temporal model for the AEGISS data. With public health authorities being notified, attempts to stop emerging outbreaks can be made, thus meeting the original goals set by the AEGISS project. The model is useful in its own right as a time-series model in similar situations where the time series of events are available.