A meta-analysis of the effect of dose and age at exposure on shedding of Mycobacterium avium subspecies paratuberculosis (MAP) in experimentally infected calves and cows

Summary

A meta-analysis was performed using all published and one unpublished long-term infection-challenge experiments to quantify the age- and dose-dependence of early and late shedding of Mycobacterium avium subsp. paratuberculosis (MAP) in cattle. There were 194 animals from 17 studies that fulfilled the inclusion criteria, of which 173 received a known dose of MAP and 21 were exposed naturally. Results from parametric time-to-event models indicated that challenging older calves or using multiple-exposure experimental systems resulted in a smaller proportion and shorter duration of early shedding as well as slower transition to late shedding from latent compartments. Calves exposed naturally showed variable infection progression rates, not dissimilar to other infection routes. The log-normal distribution was most appropriate for modelling infection-progression events. The infection pattern revealed by the modelling allowed better understanding of low-grade endemicity of MAP in cattle, and the parameter estimates are the basis for future transmission dynamics modelling.

INTRODUCTION

Mycobacterium avium subsp. paratuberculosis (MAP) is a bacterial pathogen of the ruminant gastrointestinal tract that can cause persistent diarrhoea and eventual death due to malnutrition [1, 2]. The potential link between MAP and human Crohn's disease makes the high prevalence of MAP in meat- and milk-producing animals of concern to human health [3]. Sensitivity of bacterial-culture-based screening tests is limited in early infection stages due to low or intermittent shedding of bacteria. Immune response-based serum tests are also limited due to the substantial delay between infection and consistently positive serology [4, 5]. Because the contribution of these early shedding animals to infection transmission is potentially important, understanding shedding patterns of recently infected animals is essential for designing and predicting the impact of control strategies.

Age at exposure and dose received could influence pathogenesis of MAP infection in cattle [6, 7]. Calves artificially challenged with high doses of bacteria have been reported to become infectious more rapidly relative to calves challenged with low doses of bacteria [4, 7]. However, the relationship between challenge dose and progression to infectiousness has not been fully quantified. Dose-dependent or age-dependent response to infection is common for many pathogens, including MAP [8–10]. Previous work with other pathogens illustrates the potential impact of changes to pathogenesis due to age at exposure subsequently resulting in a change in infection transmission dynamics in a population [11].

Transmission of MAP is assumed to be primarily from infectious adults to susceptible young animals, and control of MAP within farms currently involves a twofold approach of testing and removing infected adult animals and increasing hygiene on the farm to limit contact between calves and faecal material of adult animals [12]. It is generally assumed that poor diagnostic-test sensitivity [13] leading to incomplete culling where some infectious animals remain in the herd and environmental persistence of MAP bacteria [14, 15] contribute to the sustained prevalence of MAP in herds despite intervention attempts. However, our previous series of mathematical models indicated that, with current assumptions of shedding patterns, infectious contributions of adult shedders alone were insufficient to explain infection persistence and the observed pattern of infection prevalence [16]. The models indicated that an additional contribution from infectious calves could be important and in some situations dominate within-herd transmission in low-prevalence herds.

In ordinary differential equation (ODE)-based mathematical models of infection dynamics within herds, as in our previous work [16], modellers assume a constant rate of exit from each infection compartment. This simplifying assumption limits model complexity and results in exponential decay of the population within each infection stage over time. Changing the assumption of constant rate of exit can have a dramatic effect on the stability of infections within simulated populations. A variable rate of exit has been shown to more accurately predict the basic reproduction ratio, R ₀, and risk of stochastic fadeout [17]. The nature and heterogeneity of infection progression are highly influential on infection dynamics [17]. This heterogeneity may change the efficacy of intervention strategies being evaluated.

To evaluate current assumptions of constant rate of exit and to estimate age- and dose-dependent shedding patterns, we performed a meta-analysis of all available experimental infection trials of MAP in cattle. We determined the rate of entry and exit from shedding and non-shedding compartments following a challenge infection of calves and cows with known quantities of MAP. We assessed the effect of age at infection, challenge strategy and dose on time to shedding and duration of MAP shedding. We also analysed the fit of exponential time-to-event models and compared these to other distributions to ascertain whether the assumption of constant exit rates from compartments was valid. Finally, we discussed the application of the current research to adapt the mathematical model of MAP transmission on commercial US dairy farms [16] to age- and dose-dependent durations of shedding categories.

METHODS

Data sources

Literature search on PubMed (www.pubmed.org) identified 16 studies that fulfilled inclusion criteria outlined below. All literature searches and evaluations to identify, appraise and select primary studies were performed by a single author. Papers were identified in PubMed using the following combinations: ‘paratuberculosis’ or ‘Johne's’ or ‘johnei’ and ‘experimental’ and ‘cow’ or ‘cattle’ or ‘calf’. Abstracts identified by these searches were used to screen for papers in which authors performed experimental infections in cattle. Papers with evidence of experimental infection of cattle in the abstract (even if the faecal shedding was not the focus of the study) were screened in detail to evaluate whether inclusion criteria were met. If insufficient details were present in the abstract to determine whether papers tracked faecal shedding over time, the entire text and figures were evaluated. If multiple papers were identified using the same group of experimentally infected cattle, these animals were only represented once. Review papers were not eligible for inclusion, but papers referenced in a review paper were eligible to be included even if they did not appear in the original search criteria. Studies published in languages other than English were eligible for inclusion if found in the original PubMed search or from citations in review articles. Those papers which were not identified in the PubMed search but were cited in reviews were requested from the Cornell University Library network and screened with the same criteria. Additionally, a cited-reference search was carried out in Web of Knowledge (http://www.isiwebofknowledge.com/) to identify other eligible papers which cited early experimental infection studies. We contacted MAP experts (including primary study authors) to identify other studies with available data. Personal communication and the Proceedings of the International Colloquium on Paratuberculosis provided data from one additional study (see Table 1).

Table 1. Challenge and animal characteristics in the studies used for the analyses

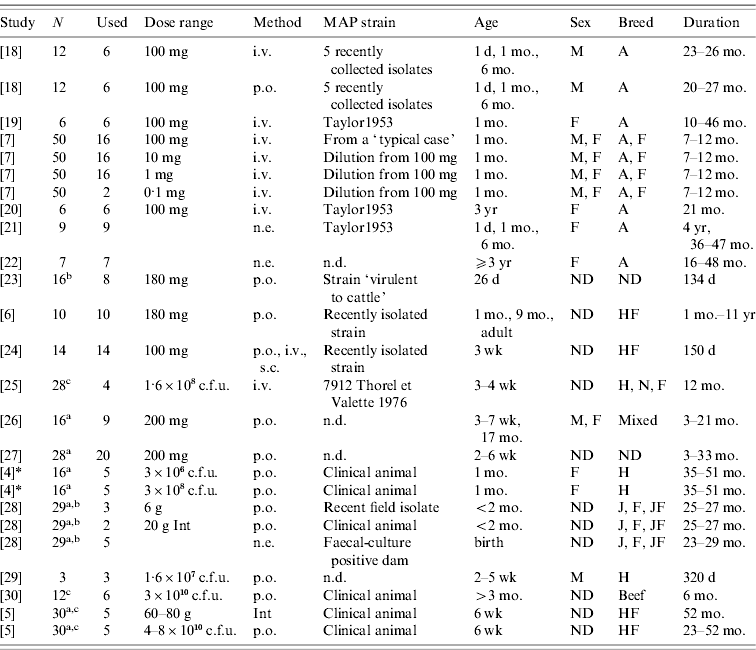
N, Number of animals in the study.

Used: Number of animals used in this analysis

(^a additional animals were uninfected controls; ^b additional animals were vaccinates; ^c strains from different species used on the remaining calves).

Dose range: Either grams wet weight or colony-forming units (c.f.u.) depending on individual study. Animals dosed with ground intestine (Int) from clinical animals were considered distinct from animals dosed with cultured bacteria.

Method: Method of dose delivery. Intravenous (i.v.), subcutaneous (s.c.), natural exposure-contact with clinical animals (n.e.), oral (p.o.).

Strain: MAP strain was often unspecified or noted as a recently isolated strain only. Taylor1953 is a strain used for the Rankin studies isolated previously (n.d., no data published).

Age: Age at initial infection.

Sex: Male (M), Female (F) or not designated (ND).

Breed: Ayrshire (A), Friesian (F), Holstein (H), Holstein-Freisian (HF), Jersey (J), Normandy (N), Jersey-Friesian crossbred (JF), Mixed, not designated (ND), beef calves (non-specified).

Duration: Amount of time animals were enrolled in the study.

* Collins, MT. Lifetime faecal culture data on all animals from [2]. Personal communication to R. M. Mitchell on 1 June 2006.

Inclusion/exclusion criteria

Because of limited correlation between quantitative value of serological tests and infectiousness as assessed by colony-forming units per gram of faecal material in recently infected animals [4, 5], studies were included only if faecal culture data was presented. Minimum study duration for inclusion in our analysis was 5 months. Data had to be presented in the paper for intervals ⩽1 month's duration, or data had to be presented for the month at first positive sample for animals sampled at intervals ⩽1 month's duration. If data was collected monthly at initiation of the study and subsequently the culture intervals were increased, the dataset was truncated to only include the monthly data points. Contaminated culture data was treated as no value rather than as positive or negative. If there was a transition between categories which included contaminated cultures, the midpoint of the time period between two available cultures was assumed to be the time of transition. In studies which included multiple different challenge strains, only those animals identified as infected with bovine-specific MAP strains were included. Animals from farms with known MAP-positive animals or animals born from infected dams were excluded from the dataset with two exceptions: Taylor et al. [18] and McDonald et al. [28]. In the McDonald et al. study, dams of calves enrolled in the study were test-negative at the time of study initiation but calves were not specifically from a MAP-free herd. Calves from dams that were subsequently test-positive were removed from the known-dose analysis. In the Taylor et al. study, animals were cited as from a herd with very low incidence of clinical disease [18]. Animals receiving vaccinations against MAP were excluded.

To evaluate on-farm infections compared to experimental infections, studies in which animals were exposed to clinical or shedding animals (defined as ‘natural exposure’) were included for a secondary analysis provided they met all other inclusion criteria. The calves in the McDonald et al. study [28] born to culture-positive dams were included in the natural-exposure portion of the study.

Standardization of experimental data across studies

If faecal cultures were recorded at intervals more frequent than monthly, all samples within a month were included in the determination of binary shedding/non-shedding status for that interval. For the Collins & Zhao study which sampled animals every 28 days [4], time intervals were converted to months. Faecal-culture technique depended on author and year of study. The sensitivity of culture was expected to be influenced by culture method and laboratory; however, quantitative information on culture sensitivity by laboratory/specific method is lacking and changes in culture sensitivity were therefore not accounted for in the analysis. If animals were given two or more infectious doses of MAP in a short period of time and faecal cultures were reported in months post-exposure, we assumed that values of time since infection were reported as time since first dose [4, 5, 26–30].

Model of MAP infection compartments

Infection compartments (Fig. 1) were defined by culture status of animals based on Mitchell et al. [16] with the addition of a slow-progressing latent compartment. This slow-progressing latent compartment accounted for animals which never entered the early shedding stage. A very similar model structure has been used to analyse bovine tuberculosis experimental-infection data and in human tuberculosis [31–33]. Presence of two distinct risk periods for shedding MAP in experimentally infected calves, one shortly after inoculation which is not associated with clinical disease [4, 5] and one period later in life which often is associated with clinical disease [2], provides the basis for our assumption of early and late-shedding stages. The possibility that animals do not experience early (detectable) shedding but enter a slow-progressing latent period before late shedding is considered based upon findings that some infected animals remain tissue culture-positive following an extensive period of time without detectable MAP shedding [20, 28].

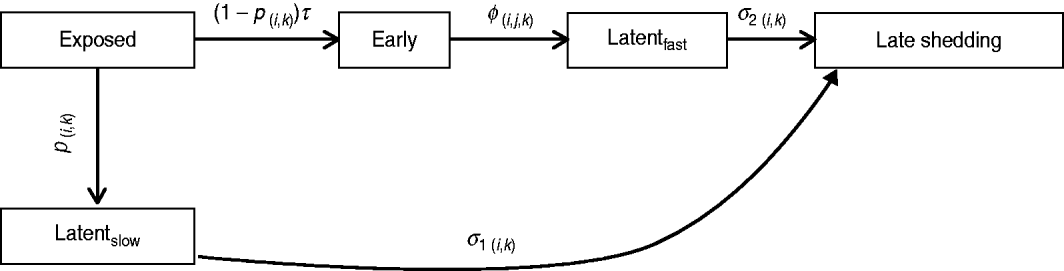
Fig. 1. Graphical representation of MAP infection compartments. Exit from exposed compartment is divided into a portion becoming early shedders (1 – p) at rate τ and a portion becoming slow-progressing latents (p). Exit from exposed is dependent on age at infection (i) and dose method/strategy (k). Exit from early shedding (φ) is dependent on age (i), dose (j) and method (k), while exit from both latent categories, fast-progressing latent (σ₂) and slow-progressing latent (σ₁), is only dependent on age (i) and dose method (k).

For this analysis, shedding must have occurred within 12 months following challenge infection to be termed early. Exit from early shedding (φ) into the fast-progressing latent stage was defined as a 2-month period with negative culture data. Any shedding following entry into the fast-progressing latent compartment was interpreted as entering the late-shedding compartment (σ₂), even if it began within the first 12 months following exposure. Entry into late shedding was the last event considered for this analysis.

Classification of animals across multiple studies

There were a total of 194 eligible animals from 17 studies, of which 173 were infected with a known dose of bacteria and 21 were exposed via cohabitation with infectious animals (natural exposure) (Table 1). Number of animals differs by compartment based both on individual study duration and infectious progression. Studies used multiple classification schemes to quantify challenge exposure: milligrams wet weight of bacteria, colony-forming units (c.f.u.), grams of intestine from clinically ill animals. Similarly, delivery methods of infectious doses of bacteria depended on the individual study and included intravenous (i.v.), subcutaneous (s.c.) and oral (p.o.). Although animals that were challenged with ground intestine from clinical animals as infectious material were dosed orally, this dosing method was treated as distinct from other forms of oral dosing due to inability to precisely quantify c.f.u.s delivered. Dose was analysed initially both as a continuous and a categorical variable. We categorized challenge doses into low (⩽10⁷ c.f.u., n=23), medium (>10⁷ to <10⁹ c.f.u., n=28) and high (⩾10⁹ c.f.u., n=122) by converting milligrams wet weight of bacteria into c.f.u. via the conversion method published by Whittington et al. [15]. The categories were assigned based on data distribution, with most animals receiving between 100 and 300 mg wet weight bacteria as an infectious dose. Dosing method was included as a categorical variable in the regression models with intravenous dosing as the baseline. Sixty-three animals were given multiple (3–5) doses of MAP over 1- to 7-day intervals (3–28 days total time between first and last dose received). Multiple exposure was included in all initial regression models (see below) as a categorical variable with single exposure as the baseline. Age was evaluated as both a continuous and a categorical variable with categories based on age at first exposure. The selection of categories was based on previous assumptions that as animals age they become more resistant to infection. Age category 1 was animals <3 months old (n=145), age category 2 was animals ⩾3 months but <3 years (n=18), and age category 3 was all animals ⩾3 years (n=10). In the models with age as a continuous variable, animals identified as adult [22] without specific age definition were assigned an age of 36 months. Calves identified as weaned beef calves [30] were assumed to be aged between 5 and 12 months and were assigned an age of 6 months (category 2).

Time-to-event statistical models

Data was described using non-parametric Kaplan–Meier curves in Intercooled Stata 10 (StataCorp, USA). Univariate tests of equality were performed by age category, dose category and multiple exposure (yes/no) for each infection compartment. Animals were treated as independent without regard to within-study clustering. Wilcoxon–Breslow–Gehan tests of equality were used to identify differences at a univariate level.

Parametric time-to-event regression models were used to determine the most likely distribution of transition rates between compartments (Stata command: streg). The youngest age, highest dose, single-exposure infections with intravenous bacteria were baseline categories for all preliminary models. To evaluate the population that never experienced early shedding, exit from exposed was modelled in a split-population time-to-event regression model (Stata command: lncure). This divided the population into animals at risk of becoming early shedders while in the exposed (1 – p) compartment with the remaining animals entering directly into the slow-progressing latent compartment by default (p).

Most of the published studies used in our analysis did not provide quantitative information on infectiousness of animals; typically only presence/absence of cultured MAP bacteria was reported. Therefore we determined shedding as a binary event without including additional information on quantity of shedding during infectious periods.

Study was perfectly correlated with age and dose in most instances, thus including study as a fixed effect in the analysis to account for differences in culture techniques and challenge-dose quantification would not meaningfully correct for experimental techniques used. Rather, intra-study correlation was addressed by including robust standard errors in all models. Robust variance was estimated through the Huber–White sandwich estimate of variance [34]. Using this method, individual observations were assumed to be correlated within clusters, but clusters themselves were assumed to be independent of one another (i.e. no between-study correlation) [35]. Using the robust clustering method, a single study with aberrant findings had less leverage than if individuals from that study were included without adjustment for intra-study correlations.

Time to event for individual i (T _i), depended on explanatory variables (β_kX _ik) including the intercept (i.e. constant, β₀) and the expected distribution of residuals for a baseline individual for each distribution tested (σε_i). In a log-normal model, ε_i has a normal distribution with constant mean and variance and ε_i are independent [36]. For the exponential model, σ is fixed at 1·0 and ε_i are also independent but in this particular model, ε_i had an extreme-value distribution. Clustering was accounted for by evaluating correlation matrices within studies, so that σε_i was a complex error that represented the correlation matrix multiplied by a residual term [37]. Time-to-event models evaluated were accelerated failure-time models (AFT) with the generic formula for expected value shown in equation (1):

(1)

For the mixed-population model to model exit from the exposed category, two distributions were added: one for a population with no risk of becoming early shedders (p), and one for a population at risk (1 – p) of becoming early shedders. Animals in the population that transitioned into the early shedding compartment (1 – p) exited exposed at a rate dependent on the log-normal distribution and their covariates. All those remaining in the exposed category at 12 months (p) moved into the slow-progressing latent category. Therefore expected time to event for an individual (T _i) was either 12 months with a probability (p) or with probability (1−p) as in equation (2).

(2)

Evaluating model distributions

For the split-population model for exit from exposed compartment, only the log-normal distribution could be evaluated due to software limitations. For all other models, the hazard function was estimated using maximum-likelihood estimators to select the best representation of duration of stay in a compartment. Five statistical distributions were evaluated: exponential, Weibull, log-logistic, log-normal and generalized gamma. Age, dose and method of infection were included in all initial models and non-significant parameters were removed in a stepwise backwards fashion. If any age or dose category was significant, then all three age or dose categories were maintained in the final model. When models were nested, model fit was hierarchically tested by likelihood ratio statistics. Akaike's Information Criteria (AIC) and plots of cumulative hazard vs. Cox–Snell residuals were used to select the most appropriate overall model distribution.

Single- or multiple-dose infection strategies relative to natural-exposure studies

One of the applications of our regression model is the evaluation of experimental doses relative to an unknown dose provided through chronic exposure which occurs in natural-exposure studies. Three natural-exposure studies were used for estimation of challenge dose [21, 22, 28]. In two of these studies susceptible animals were housed with multiple clinical and high-shedding animals [21, 22]. In the most recent study, calves were born to and/or nursed by shedding dams [28]. Progression through infection compartments was graphically compared between experimental infection strategies (single- and multiple-exposure) and the unknown challenge of natural exposure. Kaplan–Meier curves were constructed to evaluate the rate of transition between infection compartments. Separate curves were plotted for known experimental doses and unknown doses via natural exposure.

RESULTS

Description of the study population

Median follow-up in the exposure category was 3 months (range 1–12 months), and 74% of animals (n=128/173) entered early shedding within this time. Median follow-up in the early shedding compartment was 2 months (range 1–38 months), and 44% (56/128) of animals entered the fast-progressing latent state within this time. Median follow up in the fast-progressing latent compartment was 4 months (range 2–48 months), and 41% (23/56) of the fast-latent animals entered late shedding. Median follow-up in the slow-progressing latent compartment was 10 months (range 2–42 months), and 36% (9/25) of these animals entered late shedding. The proportion of animals shedding at each sampling time ranged from zero to nearly half of animals depending on time post-exposure, with peaks at 3 and 36 months post-exposure (Fig. 2).

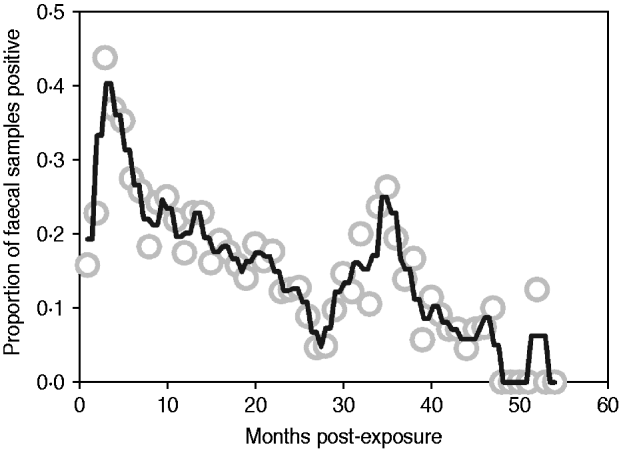
Fig. 2. Proportion of animals with a positive faecal sample each month following exposure across all studies. Grey circles indicate monthly proportion of shedding animals. Black line represents the smoothed running average (nearest neighbours). Contaminated samples are excluded from the denominator.

Time-to-event models

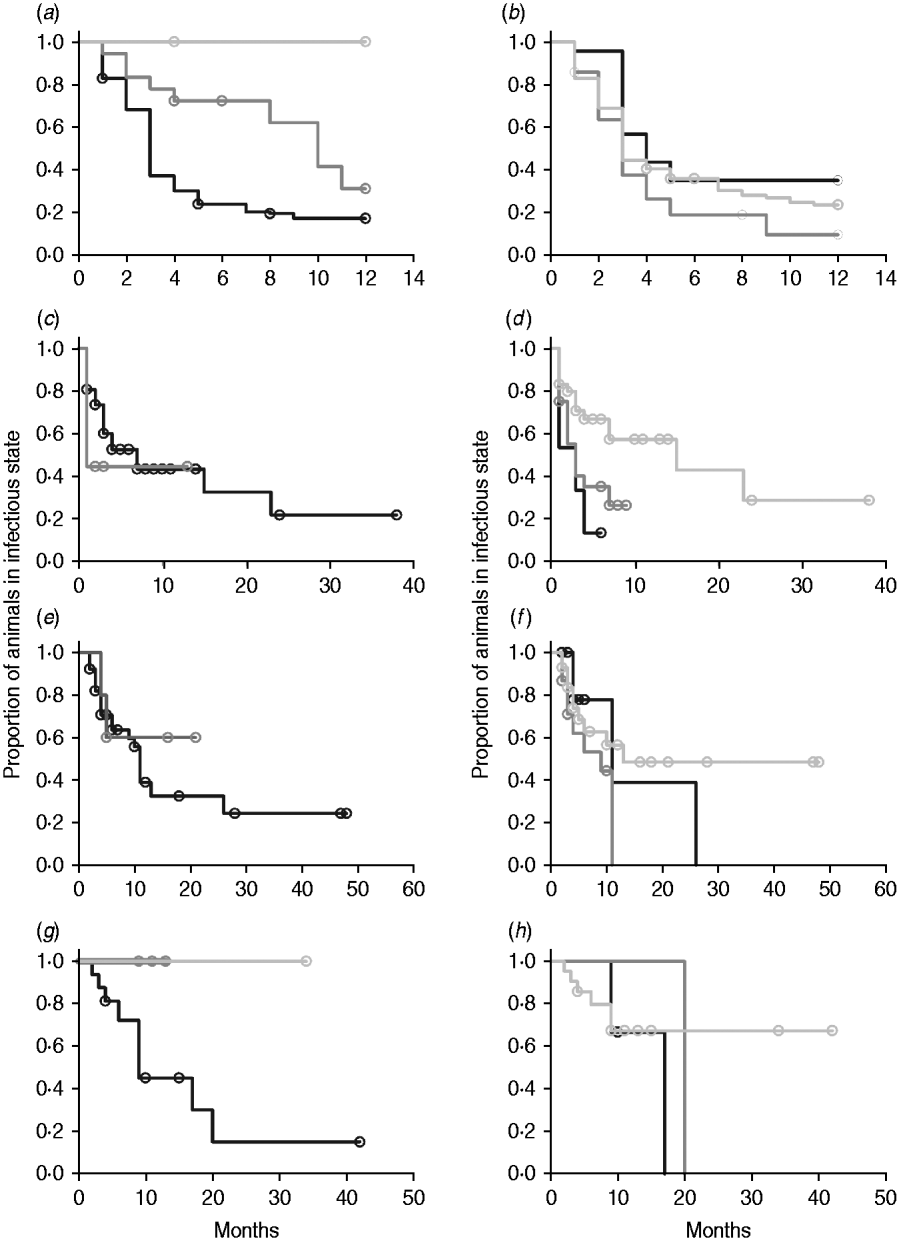
In non-parametric analysis of duration in infection categories using Kaplan–Meier curves (Fig. 3) as well as univariate Wilcoxon–Gehan–Breslow statistics (Table 2), age at infection played a role in rate of exit from all categories except exit from fast-progressing latent. Challenge dose was only important in early shedding duration. Multiple exposure increased rate of exit from both the exposed and slow-progressing latent compartments (Fig. 3). The majority of young and intermediate-aged animals shed MAP within 12 months of exposure (Fig. 3 a).

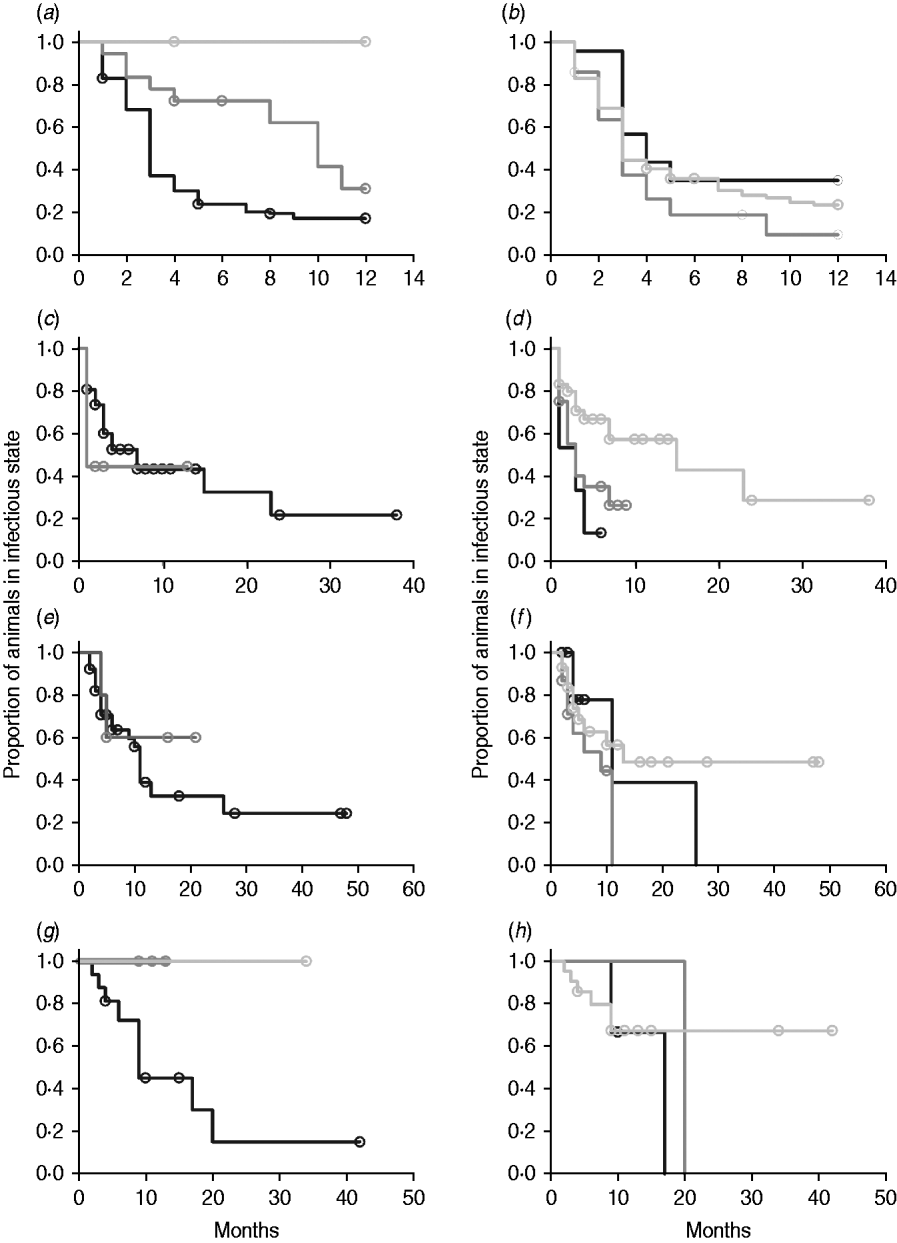
Fig. 3. (a–h) Kaplan–Meier plots of duration within infection categories: (a, b) exposed; (c, d) early shedding; (e, f) fast-progressing latent; and (g, h) slow-progressing latent. Left panels (a, c, e, g) are stratified by age at challenge (category 1, <3 months; category 2, 3 months-1 year; category 3, >1 year). Right panels (b, d, f, h) are stratified by challenge dose (category 1, ⩽10⁷ c.f.u.; category 2, >10⁷–10⁹ c.f.u.; category 3, ⩾10⁹ c.f.u.). Black line, category 1; dark grey line, category 2; light grey line, category 3.

Table 2. Description of data and univariate analysis

N is the number of animals that enter the category. The number which exit due to a shedding event (begin or stop shedding, depending on the compartment) is indicated for each shedding compartment. P value is for a univariate Wilcoxon–Breslow–Gehan test of equality for each category of interest (age, dose or multiple exposure).

In parametric time-to-event models, animals exposed at a young age (category 1, black line) exited rapidly from exposed (with rate τ) and from slow-progressing latent (with rate σ₁) compartments (Fig. 3 a, g) and spent longer in the early shedding category (Fig. 3 c) than animals exposed at older ages. Challenge dose only increased time in the early shedding category (Table 3 b). Multiple dosing decreased the time spent in the early shedding category and increased time spent in all non-shedding categories. Oral dosing caused more rapid entry into early shedding, and, in addition, greatly increased the duration of the non-shedding, slow-progressing latent compartment. Subcutaneous dosing increased rate of exit from early shedding and decreased rate of exit from the fast-progressing latent category. Overall these changes served to decrease the total portion of time that a recently exposed animal would be shedding.

Table 3. Regression coefficients, robust standard error and statistical significance for all log-normal time-to-event models*

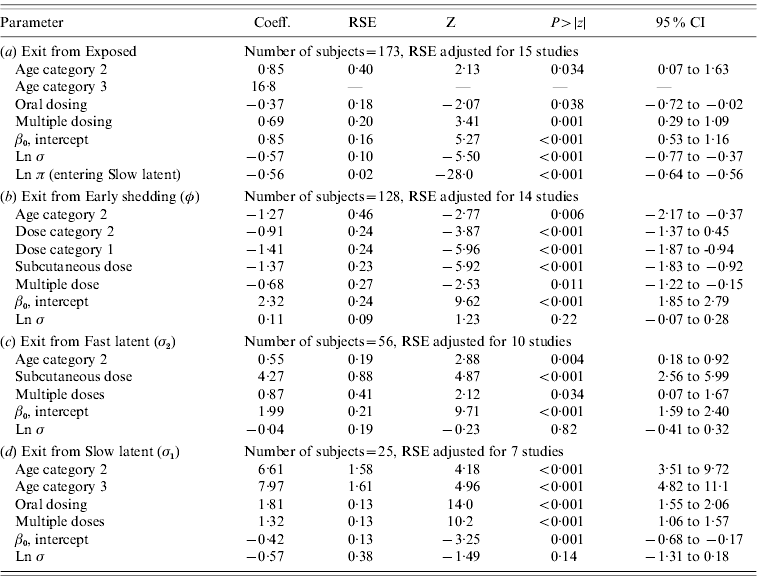
RSE, Robust standard error; CI, Confidence interval.

Observations and clusters taken into account for RSE estimation are noted.

σ is the model error multiplier.

Ln π is the log of the probability of entering incubation in the split-population model.

* Baselines are age category 1 and dose category 1.

The split-population model estimated that 55% of animals did not develop detectable early shedding (p) or shed only for a short time period, and the remainder of animals (1 – p) from the exposed category entered early shedding in an age-dependent manner (Table 3 a). The highest risk of entry into early shedding was among the youngest animals and there was a zero risk of early shedding in adults.

Models using dose and age as continuous variables rather than categorical variables produced estimates that were broadly similar with respect to age and challenge dose except in the case of exit from fast-progressing latent category (data not shown) for which age and dose were significant only in the continuous models. Values of predictors were not linear with age or dose for any categorical model and therefore results presented are for categorical models.

Goodness-of-fit and comparison of statistical distributions

Goodness-of-fit statistics for the best-fitting distributions for each state transition are presented in Table 4. Gamma distributions did not converge for all models except exit from slow-progressing latent category, whereas log-logistic and Weibull typically showed a poor fit to the data. Log-normal models had lower AIC than exponential models for all categories, indicating a superior fit despite the extra degree of freedom in log-normal models relative to exponential models. Transition from slow-progressing latent category (σ₁) was best modelled with a log-logistic distribution.

Table 4. Goodness-of-fit of modelled distributions in time-to-exit models for each of the four infection categories

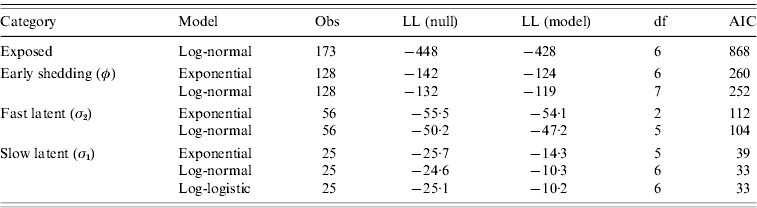
Values presented are consistent with the categorical models from Table 3.

Evaluation of log-likelihood (LL) in both the null and full models, number of observations (Obs), degrees of freedom (df), and Akaike's Information Criteria (AIC) from all final models.

Plots of cumulative hazard vs. Cox–Snell residuals of the exponential and log-normal models were compared by visual inspection (Fig. 4). Because most of the residuals were small, the distributions of residuals were heavily skewed towards the origin. There was little difference between the residual plots from exponential and log-normal hazards (Fig. 4 a–c). The only substantial difference observed in model fit was for exit from slow-progressing latent category, where the exponential model produced high estimates for duration of slow-progressing latent well beyond the lifespan of a cow. Note that when comparing log-normal and exponential models with the same mean, the median is higher in the log-normal model.

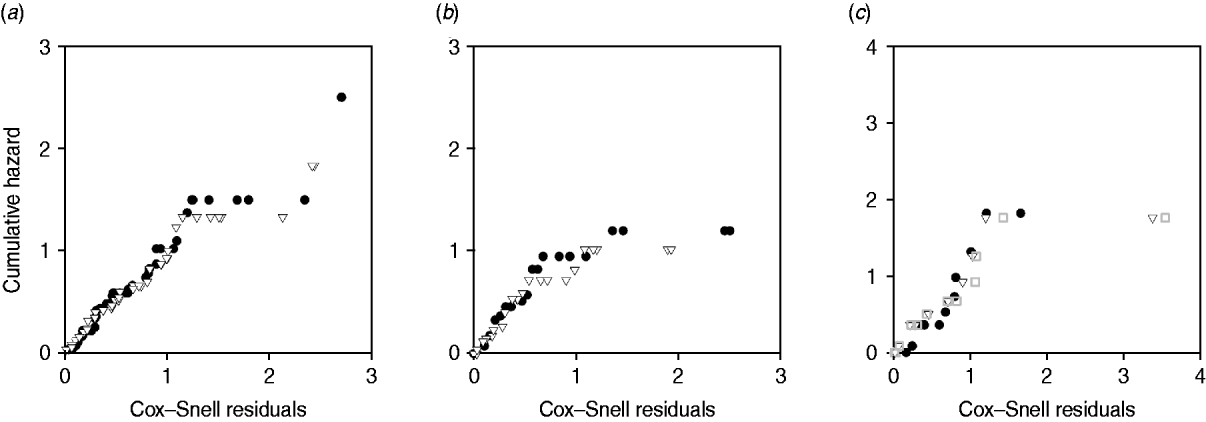
Fig. 4. Plot of Cox–Snell residuals vs. cumulative hazard for (a) exit from early shedding, (b) exit from fast-progressing latent and (c) exit from slow-progressing latent. Closed circles represent residuals from best-fitting exponential models and open triangles represent residuals from best-fitting log-normal models. The open grey squares represent the best-fitting gamma distribution in exit from slow-progressing latent (c). A model which fit the data well had data points on a 45° slope without strong deviations [38].

Natural-exposure infections

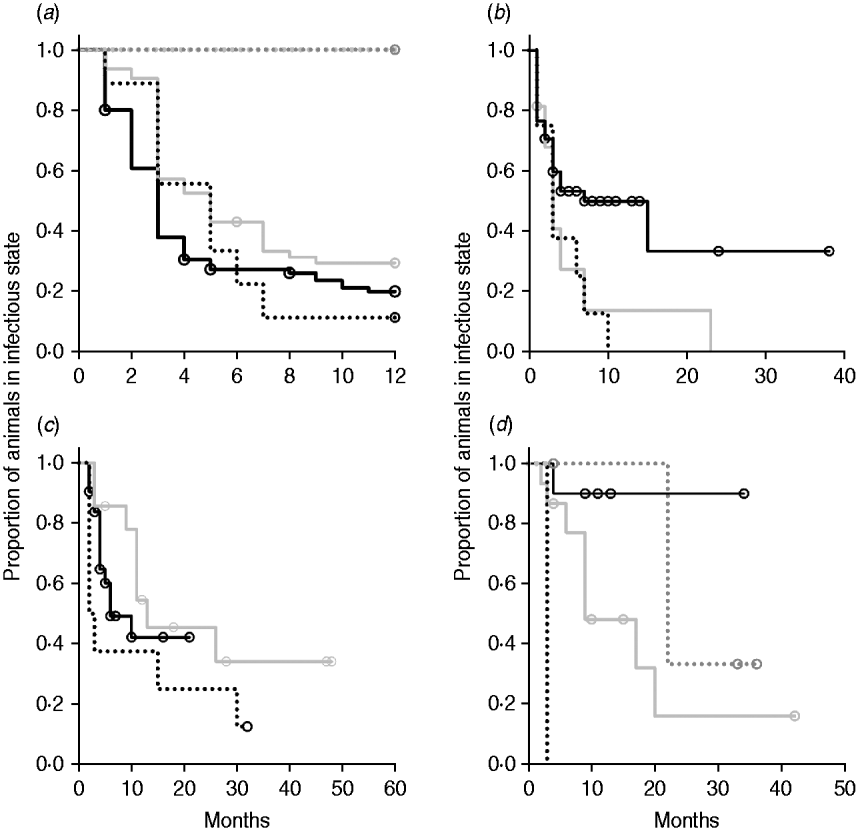
Kaplan–Meier plots of exit from exposed category in natural-exposure infections of young animals were similar to those for experimentally exposed animals (Fig. 5 a). Exit from early shedding category in natural-exposure infections of young animals described by Rankin [21] was similar to plots of animals exposed multiple times (Fig. 5 b). Exit from fast-progressing latent category in these data was more rapid within the first 10 months than for both classes of experimentally exposed animals (Fig. 5 c). There were insufficient natural-exposure animals in the slow-progressing latent compartment to assess whether the fit of exit is closer to multiple-exposure or single-exposure experimental animals. The natural exposure of calves appears lower in the study by McDonald et al. [28] (Fig. 5) compared to the study by Rankin [21]. Adults with natural exposure [22] only shed late following infection, which is consistent with the behaviour of adults in experimental dosing regimens.

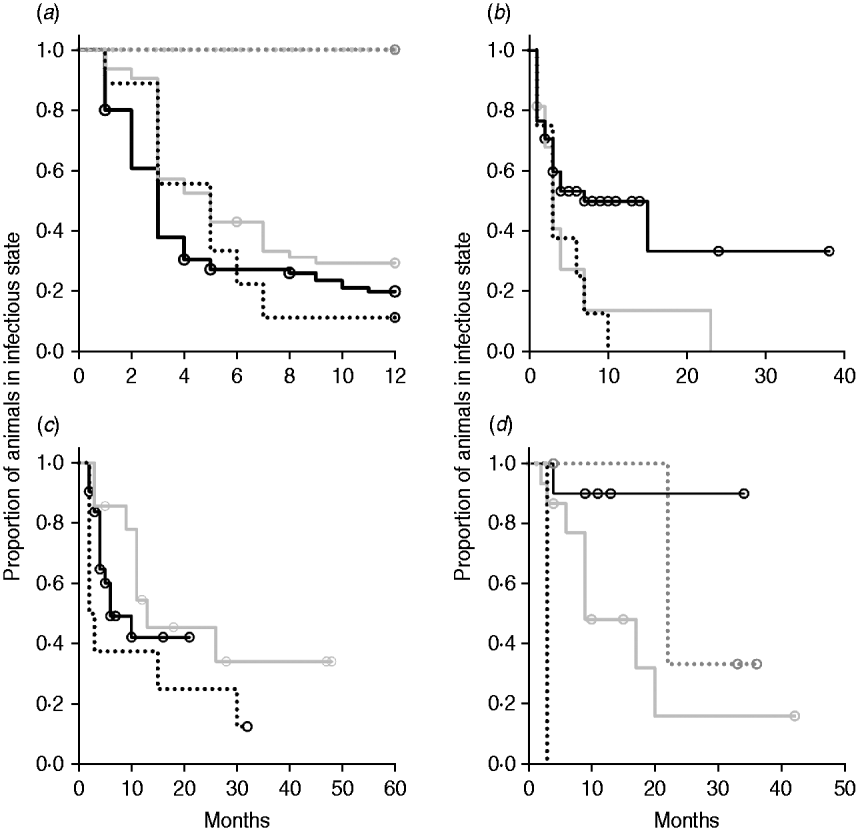
Fig. 5. Kaplan–Meier survival plots for (a) exit from exposed and (b) exit from early shedding, (c) fast-progressing latent and (d) slow-progressing latent by exposure strategy (single or multiple dose). Solid lines indicate different exposure categories; black lines indicate single-exposure infections and light grey lines indicate multiple-dose exposures. Dotted lines indicate studies of natural-exposure infections (absolute dose unknown) from three specific studies: black dots [21], dark grey dots [22], light grey dots [28].

DISCUSSION

Experimental infections with known doses

This paper provides a more robust estimate of duration of stay in infection compartments than was previously available for long-term experimental infection studies of MAP in cattle. Our analysis included all long-term infection studies in cattle from the recent literature reviews by Begg & Whittington [39] that fit the study criteria identified in the Materials and methods section. Many, but not all, of the studies that we used were published in peer-reviewed journals. The studies used in this analysis provided a wider range in age of animals at time of challenge and a wider range of challenge dosages than any single study could address.

Early shedding followed by a long duration of non-shedding is common in experimental infections (Fig. 2) but early shedding is not usually addressed in models of MAP dynamics. Recent epidemiological studies also indicate that the assumption that young animals are not shedding needs to be challenged [40]. Not only do young animals shed MAP following exposure, but they are also capable of transmitting MAP to other calves [41]. The alternative to considering the independent early shedding period is to consider all the shedding animals in one population. This means that an animal which sheds in the first 12 months will be considered a shedder throughout its entire life, which is not an adequate reflection of either the experimental or the observational data available. This paper serves to quantify the early shedding phase.

Median time to first shedding in animals that shed shortly after infection is 3 months. Reducing the time period for which animals were eligible to become early shedders to 6 months would have captured the majority of early shedding animals (Fig. 3 a), but left a population which shed briefly early in life in the late-shedding category despite subsequent cessation of shedding. Only a small percentage of infected animals are shedding when they enter the lactating herd, while in the dataset used in this meta-analysis more than half of calves exposed in the youngest age category have an early shedding phase. This population should not be contributing the same amount to infection transmission as animals which are culture positive and often clinical in the late-shedding stage [2].

Including studies with a range of dosing methods but allowing for dose method as a parameter in the analysis increased sample size while controlling for artefacts. Infection progression was influenced by dose method, with oral dosing increasing rate of exit from exposed category, but increasing duration of stay in the slow-progressing latent population. If oral dosing presents a risk of transient shedding due to intestinal burden of the infectious dose [42], these would both be expected findings. Animals would be more likely to shed early after exposure, and the population of animals which did not shed early (which one could hypothesize received a lower infectious dose than those that did shed early after exposure) would remain non-shedding for longer. The clear difference in infection progression between subcutaneous dosing and baseline intravenous dosing could be interpreted as decreased efficiency of initial infection due to the regional deposition in an area which is not a reservoir for MAP in infected animals. Despite the extremely large doses of ground intestine given, the c.f.u.s delivered could be lower than assumed in this analysis, which placed all ground intestine dose mechanisms in the high-dose infection category due to sheer volume of infectious material delivered.

Multiple-dose models have a prolonged time of exposure relative to single-dose infections. They may present a model of chronic exposure rather than be equivalent to a single large dose. Duration of the multiple-dose infections in these studies ranged from 3 to 28 days, which is still a fairly narrow window of exposure relative to the lifetime exposure in a commercial dairy herd. The overall effect of multiple dosing was to decrease the time spent in potentially infectious categories. In Kaplan–Meier plots of exit from slow-progressing latent (Fig. 5 d), it appears that multiple-dose exposure causes a slower exit. However, this population includes multiple animals in the oldest age category which is taken into account in the multivariate analysis (Table 3). Because all animals infected with ground intestine were in the multiple-dose category, part of the effect of multiple dosing was that of the ground intestine dosing system. When analyses were re-run excluding the animals dosed with ground intestine (n=7), multiple dosing remained significant in all models (data not shown). Decreased time of shedding in animals which received multiple doses is similar to the pattern of shedding in animals given lower doses of MAP. This could mean that initial dose is the most important factor in infection progression. Because the longest multiple exposure period in experimental animals was 28 days, we cannot assess true chronic exposure. However, calves which were naturally exposed to MAP in the Rankin study were in with highly infectious clinical animals for multiple months and had shedding patterns similar to a moderate or highly exposed animal [21]. If chronic exposure were to result in rapid infection progression, we would expect these animals to have moved through the infection categories faster than highly exposed single-exposure individuals.

Data numbers were not balanced with respect to age of animals at time of infection. Because it is a common belief that the majority of infections happen in young animals, there have been few studies performed historically looking at experimental infection of adult cattle [20, 22]. These studies are both expensive and offer little value when working under the assumption that adults are resistant to infection. The pattern of shedding is distinct between young animals and adults, with no adult animals experiencing an early shedding period in experimental infections, and rarely entering the late-shedding period prior to 4 years post-infection. We argue that following data from the ten experimentally infected adults in the published literature provides substantial information on the trend in this population and that valid conclusions concerning the inverse relationship between age at exposure and likelihood of early shedding can still be drawn from these limited data.

Due to data availability, this analysis is restricted to observation of duration of stay in infection compartments without quantification of bacterial load. We were not able to determine if there was a change in volume of bacteria contributed to the environment while in a shedding phase. Animals that become shedders earlier in adulthood are more likely to become high shedding or clinical during their expected life in the herd [43]. It is possible that this population represents a cohort of animals which experience early shedding and moved more rapidly to late shedding than those which entered the slow-progressing latent period initially.

Our exclusion criteria eliminated animals from farms with known MAP-infected animals and animals with non-bovine-specific MAP infections. In addition, the requirement that culture data were published monthly also decreased sample size. However, in our opinion, this was a necessary step to ensure validity of results. Animals from infected dams or farms with known MAP-positive animals could have been infected any time prior to the initiation of the experimental period. Shedding patterns are influenced by host dependence of MAP strains [5, 25, 30]. Because we are interested in dynamics on farms, we chose to eliminate infections with strains which are not reflective of bovine-specific MAP infection patterns.

We could not distinguish between false negatives shedding low levels of bacteria and true negatives. It is possible that most animals shed early following infection, but that some animals are below the threshold of detection. In this case, we would have overestimated the rate of exit from early shedding, as well as overestimated time spent in the fast-progressing latent state, both serving to artificially decrease the impact of early shedding on transmission dynamics. Serial testing as performed in these experimental studies increases the sensitivity of the testing system for detecting truly infected individuals. Because animals are tested at least monthly, the sensitivity of these systems to detect any early shedding is much higher than annual testing schedules employed on commercial farms. However, duration of the early shedding period may be artificially truncated.

Because sensitivity of faecal culture increases with bacterial shedding, low shedders that are less likely to test positive are also less important for transmission. If there is truncation of the early shedding period due to test sensitivity, it represents reduction in epidemiological importance. If degree of bacterial shedding is related to infectiousness then this supports our conjecture in terms of the importance of high early shedding to herd persistence. Regardless of whether the animals in the slow-progressing latent compartment truly do not experience early shedding or are simply below the threshold of detection, our data would indicate that animals in this slow-progressing latent compartment represent a distinct population which progresses through infection stages more slowly than animals which shed early. The association between decreased risk of early shedding and prolonged time to late shedding would be important to infection dynamics.

Exponential time-to-event models are compared with the best-fitting log-normal models. Exponential models with constant risk of exit are standard assumptions for mathematical models of disease transmission, but the log-normal distribution is a better alternative to this standard. The distinction between log-normal and exponential exit rates lies in the shape of the duration of the infection states. In exponential models of exit, the rate is constant and infectious individuals have the same risk of exit immediately after entry into the infection category as they do after substantial time in the infection category. In log-normal models, individual risk of exit increases with time in category to a peak value and then decreases. This latter scenario is more realistic than constant rate of exit and was previously described for Salmonella Cerro infections [44]. Future MAP models with exponential exit rates might fail to sustain infection in small populations. Mathematical models are sensitive to both the distribution of time in category and mean time in category, with increased probability of elimination in models with a more constant time in each infection category [17]. Estimates from the exponential models give a frame of reference for future work on disease transmission where we make a choice to either use standard exponential exit assumptions or the log-normal assumptions which better match the disease process.

Natural exposure experiments

The two natural-exposure studies on young animals probably had different levels of exposure, with most exposed young animals from the Rankin study [21] shedding early, but no animals from the McDonald et al. study [28] shedding early after exposure. This variation is biologically plausible, as level of infection is determined by rate of contact and infectiousness in each situation. The McDonald et al. study focuses on a more pastoral environment [28] where rate of contact would probably be lower than in a zero-grazing facility. The enclosed animals were group-housed with outdoor access in the Rankin study as well [21]. It is possible that this housing situation more closely mimics a modern conventional dairy farm. More studies of this type would be instrumental in determining what level of transmission actually occurs on commercial dairy farms. Adult animals exposed to cows with a clinical MAP infection [22] presented themselves very similarly to adults that were experimentally infected, with no early shedding period and a long period without late shedding. Because we identified only three long-term studies with naturally exposed animals that were sampled monthly, we do not expect that they represent the full range of infection transmission patterns. Our summary data do, however, illustrate the principle that natural infections may have a much shorter time to shedding than generally assumed.

Application of findings

Age-at-exposure-dependent risk of early shedding might play an important role in transmission dynamics. In contrast to low-shedding adult animals which have only intermittent contact with young animals, young shedders are intensively mixing with susceptible young animals on most commercial dairies or in heifer-growing facilities [45]. If they are shedding at levels equivalent to low-shedding adults as found in experimentally exposed young animals [41], young calves can potentially contribute more to transmission dynamics than low-shedding adults. In addition to the high rate of contact with other young susceptible calves, our results show an inverse relationship between age at exposure and both duration and likelihood of early shedding. The effect of early shedding is not the only consequence of infection at a younger age. Those animals which enter early shedding progress to late shedding more rapidly than those which do not enter early shedding. Contributions from young high-shedding animals which become late shedders at a young age due to early exposure can perpetuate early infections through direct transmission (e.g. dam–daughter at birth, via colostrum or in utero) or indirectly through a grossly contaminated environment [46].

The combination of increased early infectiousness, higher rate of contact among young cattle and a more rapid progression to late shedding could create a forward feedback loop within a herd. Theoretically, the prevalence of infection within the population would then determine what infectious states are reached [47]. As animals are exposed at a younger age, there is increased risk of calf-to-calf transmission as well as a higher percentage of animals which are transitioning into a late-shedding phase during their time in the herd. Both the increased calf-to-calf transmission and increased number of late shedders will further increase herd prevalence. The high proportion of shedding animals could be self-propagating, so that as a herd reaches a certain prevalence of infectious animals, eradication of infected animals becomes increasingly more difficult. These exposure processes might contribute to the heterogeneity in farm-level prevalence that is a feature of MAP epidemiology [45]. These different exposure experiences may also have an important effect on the success of interventions to control disease, and might explain the persistence of MAP infection on farms undergoing control strategies. If young animals are contributing to the exposure of other young animals, we may need intervention strategies that focus on isolation of young animals at risk for shedding from the population of susceptibles in addition to removing shedding adult animals. It should be noted, however, that a recent study failed to detect faecal shedding in naturally exposed calves [48].

Impact on transmission dynamics

We have seen in previous transmission models that infectious calves can theoretically sustain infection in populations that would otherwise move towards elimination [16]. Models of transmission dynamics which lack the early shedding category defined in this analysis do not capture a potentially important transmission cycle within herds [43, 49]. Our previous models which did not distinguish infection progression patterns between animals aged <1 year also missed a component of infection dynamics [16]. Future work will incorporate both early shedding and age-dependence of shedding in animals aged <1 year. The positive feedback relationships that we have shown between age at challenge, dose received and duration in infection categories might lead to the development of scenarios in which the reproductive number of MAP is bistable depending on the initial prevalence of infection, creating the possibility of multiple endemic states.