Modelling outbreak control for pneumonic plague

Summary

Although pneumonic plague is listed by the Centers of Disease Control in the leading ‘critical biological agents’, very few studies exist on this subject. In this study, a mathematical compartment model was used to describe the geographical and temporal spread of an epidemic of pneumonic plague following its use as a biological weapon. Univariate and multivariate analyses were performed in order to assess the key parameters for the control of an outbreak in France. If interventions were taken 10 days after an attack, a reference scenario of 1000 index cases in Paris would lead to 2500 deaths. The results of the study indicate that the rapidity of onset of interventions has the largest effect on the final size of the epidemic, followed by wearing masks, treating contacts preventively and quarantine. Limiting inter-regional mixing does little to reduce casualties, although it does confine them to a single region.

INTRODUCTION

Plague is a bacterial disease caused by Yersinia pestis, that appears through three main forms: bubonic, septicaemia and pneumonic plague. The last form is considered the most dangerous for three reasons: (1) no vaccine exists, (2) rapid diagnostic tests are only available at some health departments and military laboratories, and (3) it is the only form that spreads directly between humans, at a mortality rate that increases by 100% if left untreated [1, 2]. Pneumonic plague, if used as a weapon, could cause disease and death in sufficient numbers to cripple a city or even a country [3, 4]. As it is transmitted by the respiratory route, the most likely form of attack is the release of aerosols, a mechanism that has been shown to produce disease in non-human primates [1]. A mathematical stochastic model describing the potential extent of an outbreak of pneumonic plague with a description of the natural history of the disease has recently been published [5]. The authors estimated the average duration of latent and infectious periods in order to simulate the spread of an epidemic of pneumonic plague as long as few deaths occur. However, they did not model the impact of different control measures or the geographical spread of pneumonic plague.

Interventions that were examined in our study included: use of masks, quarantine, prophylactic treatments and reduction of the spread via human travel, the last intervention possibly being of importance if the considered area is large. To evaluate the impact of interventions we built a deterministic compartmental model to study the geographical and temporal spread of pneumonic plague after an aerosol release. This model was applied to metropolitan France to predict the impact of an attack in Paris. A Latin Hypercube Sampling method was then performed on the different parameters of the model. This sampling method was used to assess the role that each simulated intervention would play in the size of the epidemic (i.e. cumulative number of deaths) [6, 7].

METHODS

The pneumonic plague spread model: a compartment model with a geographical dimension

We based our model upon the description of the natural history of pneumonic plague from Gani & Leach [5]. In the simulated population, an infectious individual meets every day c susceptible individuals, who are referred to as ‘contacts’. These contacts have a probability β, of being infected by pneumonic plague. The contamination is followed by a mean latent period of α⁻¹ days, then by a mean infectious period of γ⁻¹ days. Quantities given below are related to the basic reproduction number for pneumonic plague denoted R ₀ through the following relationship: R ₀=β.c.γ⁻¹. Death results if the individual is not treated.

Four types of interventions were modelled: wearing masks, prophylaxis of contacts, quarantine and treatment of infectious individuals, and limitation of inter-regional mixing. All were modelled as Heaviside functions; they were constant before and after the onset of interventions.

Once knowledge of the outbreak is brought to the public's attention, a percentage of the population would wear masks, leading to a reduction of the daily potential infectious contacts, quantified by the number c. Tracing contacts would lead to the identification of a proportion ρ of them, which would be assumed to be preventively treated with tetracyclins during a mean period of δ₁⁻¹ days, at a dose of 1·4 mg per individual (the data used to determine this quantity were based on the recommendations of the WHO for the daily quantities of tetracyclins to be administered to people) [2]. There is no evidence of immunity induced by the disease, and treated individuals would become susceptible again after the end of the treatment. The treatment was assumed to be 100% effective. The rate at which infectious individuals attended a hospital was assumed to be θ. There, they would be isolated and treated with streptomycin at a dose of 1·7 g per individual (again, this quantity was calculated on the recommendations of the WHO for the daily quantities of streptomycin to be administered to people) [2]. This treatment was considered effective if administered within 24 h after the onset of symptoms. The mean duration of antibiotherapy was assumed to be δ₂⁻¹ days. If the patient began treatment after 24 h, death may occur at the hospital at the rate δ₃ [2].

The population was divided into seven compartments, which correspond to the states given above: susceptible individuals (denoted S), contacts who are identified (denoted T), latent contacts who are not identified (denoted E), non-identified infectious individuals (denoted I), identified infectious individuals for whom the treatment was effective (denoted Q₁), identified infectious individuals for whom the treatment was not effective (denoted Q₂), and removed individuals due to death (denoted R).

The classical SEIRS model is considered valid as long as the hypothesis of homogeneity of the population holds. If the considered area is vast, this assumption is probably false. We can introduce a degree of heterogeneity in the model dividing the considered geographical area into smaller areas that are linked through mixing between areas. Flows to a target region for a given group are supposed to be proportional to the proportion of this group among the population of the original region. ‘Travel’ is defined as the movement of a given individual (e.g. a tourist) from one region to another. As such, once the individual has reached the target region, he/she might return to the original region after a delay of unknown duration or never return. On average, the mean duration of stay of a latent individual in a given region was long enough for him/her to become infectious there. This model is probably less valid if we take into account individuals who commute daily.

We considered in our model 21 French administrative regions (with the exception of Corsica and overseas) as sub-areas of metropolitan France. The population in each region was considered homogeneous and the model explained below was applied to describe the spread of the epidemic in each area. The inter-regional mixing from one region to another was supposed to be constituted of travels and involved individuals who were healthy enough to travel. Therefore, isolated, infectious and dead individuals did not travel. We simulated interventions consisting in reducing these flows by a fraction of λ.

All parameters of the model are listed in Table 1. The resulting system of ordinary differential equations is detailed in Table 2.

Table 1. Parameters and definitions

Table 2. Equations for the spread of the epidemic in the region j

i(t) is the proportion of infected individuals who are discovered and placed into quarantine within 24 h following the first symptoms. This can be expressed as follows:

Parameter values

For the reference scenario, we set R ₀ (the number of secondary cases infected by one single case in an entirely susceptible population), the only value we found in the literature was R ₀=1·3 [5]. The upper bound for sensitivity analysis was chosen to be 10, since we had no knowledge of an epidemic with a R ₀ greater than the bound.

The reference scenario was based on the hypothesis that an attack in Grand Paris by aerosol release would lead to 1000 index cases. This large number of cases might correspond to an attack in the subway at the rush hours. We considered that interventions would be set T ₀=10 days after this exposure. Indeed, the difficulty of identifying a disease that has not occurred recently in France might cause a delay in diagnosis and in the onset of interventions.

The initial chosen value for c was c ₀=10, corresponding to the fact that an individual has about 10 daily potential infectious contacts [6]. ρ, θ and λ which describe the interventions ‘prophylaxis of contacts’, ‘treatments’ and ‘limitation of inter-regional mixing’ were set to 0 before T ₀. After this date, the parameters took the constant values presented in Table 1.

With data obtained from the National Company for Railway Transportation (SNCF) and the French Ministry of Equipment, we used annual data for train, car and aeroplane transportation in 2001 for modelling daily flows between regions [6]. The inter-regional mixing rates were estimated under the assumption that they were symmetric. We used daily average of fluxes of passengers to run our simulations, which do not take into account seasonal or monthly variations of transport between regions. These hypotheses were made in order to conserve regional population sizes and because accuracy of the data was not good enough for better modelling.

Sensitivity analysis

We performed a multivariate sensitivity analysis with the Latin Hypercube Sampling method to assess the role that model parameters may play in outbreak control [7]. Considered parameters were the basic reproduction number R ₀, the time of interventions T ₀, c, ρ, θ and λ. 200 sets of parameters were simulated with a uniform distribution for all parameters. The bounds of distributions for each parameter are detailed in Table 1. We then estimated partial rank correlation coefficients (PRCCs) between each parameter and the total number of deaths at the end of the outbreak which gives a weight of this parameter in outbreak control.

A univariate sensitivity analysis was then performed for different values of the most significant parameter (T ₀) from the reference scenario to assess more precisely its role on the size of the epidemic and on the quantity of required antibiotics.

RESULTS AND DISCUSSION

The reference scenario would lead to an epidemic of 2500 deaths, with a duration of 27 days (see Fig. 1). The model allowed for geographical spread of the disease, which would, however, remain concentrated around Paris, where more than 70% of the deaths would be found, according to the simulations. Death rates in each region are shown in Figure 1. The model forecasts the use of antibiotics providing estimates in quantity (5000 injections of streptomycin) (see Fig. 2).

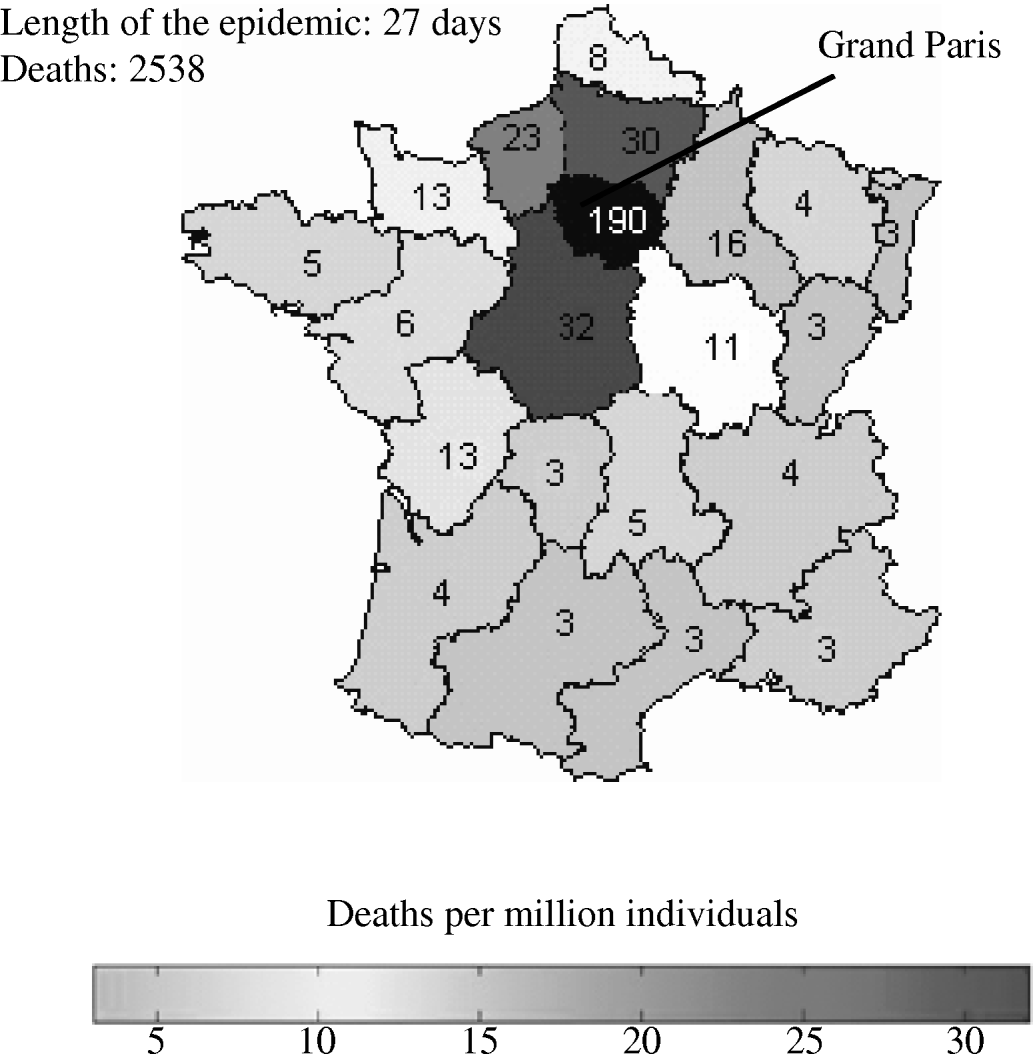
Fig. 1. Size of pneumonic plague epidemic in France for the reference scenario. The region where the attack took place (Grand Paris) is shown in black. (See Table 1 for the values of parameters employed in the reference scenario.)

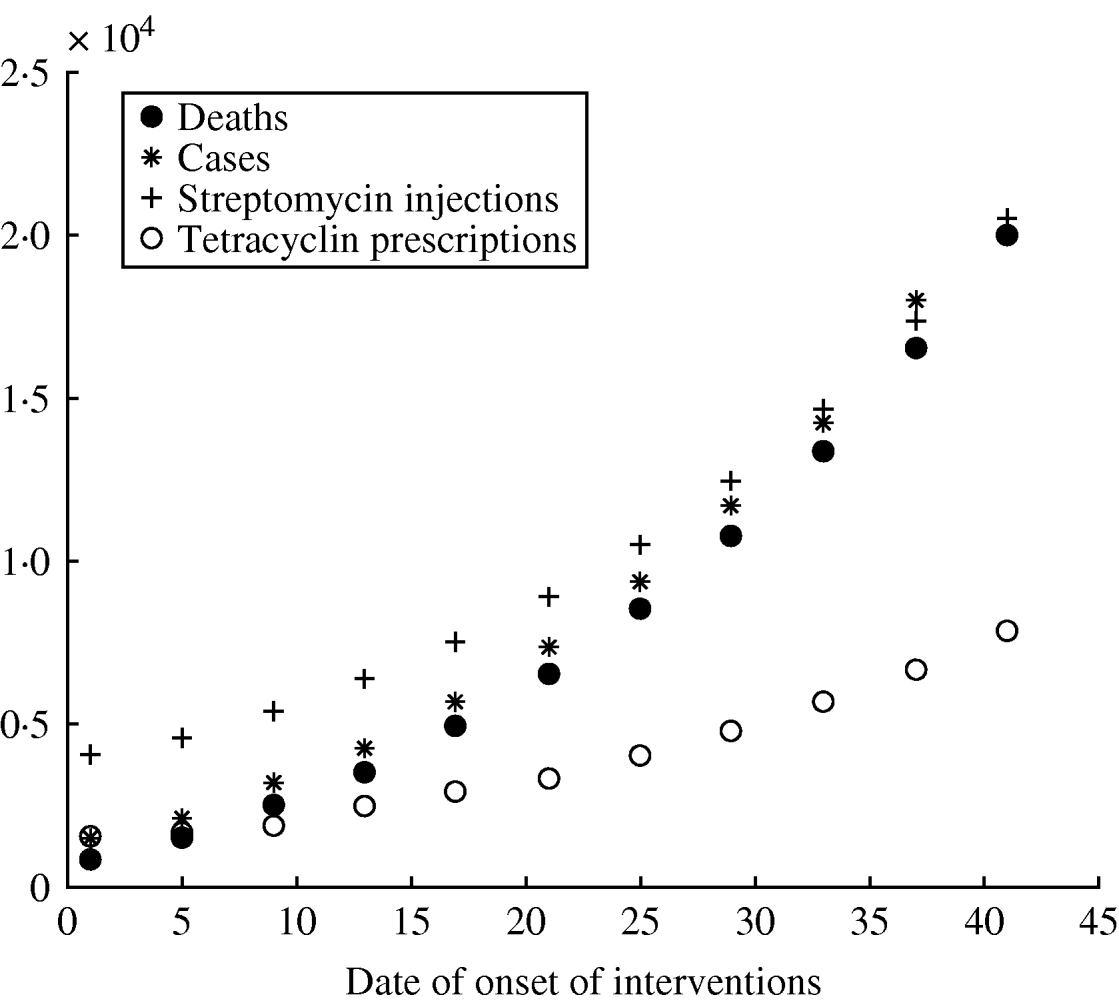
Fig. 2. Role of the date of onset of interventions on different variables for the epidemic in France. (See Table 1 for other parameter values.)

PRCCs (see Table 3) put in evidence that the value of R ₀ affects the size of the epidemic. This shows that a better estimation of its value would be necessary to estimate a precise size of an epidemic (R ₀ has the second highest value of PRCCs). Surprisingly, limiting inter-regional mixing would not have a significant effect on the final size of the epidemic. The most efficient parameter in controlling the outbreak was the time to onset of interventions. Wearing masks and a policy of tracing contacts and preventive treatment would have a significant impact on outbreak control (they have similar PRCCs), the first intervention probably being the easiest to realize.

Table 3. Partial rank correlation coefficients (PRCCs) obtained after 200 simulations

The PRCCs are computed between input values of the parameters (See Table 1 for the definition of parameters involved) and final size of the epidemic.

* Results significant at P<0·05 level.

Univariate sensitivity analysis for different values of T ₀ shows that the number of deaths increases rapidly with time to intervention, underlining the need for a quick reaction from the authorities (see Fig. 2).

We provided a deterministic model describing the spread of a pneumonic plague attack after interventions are taken. This model shows that limiting the inter-regional mixing would not have a significant impact on the size of epidemic. This intervention may, however, prove useful, since it concentrates the epidemic in the initial region, which could facilitate the work of public health services (see Fig. 3). Concerning the other interventions, our results are in line with observations made on most other pneumonic plague outbreaks before the use of antibiotics: with an efficient policy associating mask wearing and isolation of traced contacts, most epidemics were stopped quickly [8–10]. Time to intervention was the most significant parameter.

Fig. 3. Size of pneumonic plague epidemic (a) when no reductions of transports are applied and (b) when transports are completely stopped 10 days after the epidemic start.

The value of T ₀ we chose in the reference scenario was based on the fact that pneumonic plague has not occurred recently in France. This might introduce a delay in diagnosing the disease by physicians. The first deaths would probably occur 4–6 days after the attack, the important number of them in the following days leading to the identification of plague. The quantity of streptomycin required in the reference scenario might cause problems in supplying enough competent hospital staff, since streptomycin must be injected intramuscularly twice a day [2, 11]. We considered antibiotherapy with streptomycin, since this is the most effective antibiotic against plague and the drug of choice for the treatment of plague, particularly the pneumonic form [2]. However, we did not advocate the use of other alternative antibiotics recognized by the World Health Organization (WHO), e.g. fluoroquinolones. These have been shown to have good effect against Y. pestis in both in vitro and animal studies, but no studies have been published on its use in treating human plague victims [2]. Chosen values of c, and θ for the reference scenario are plausible in a country that has a good experience of pneumonic plague such as Madagascar, where most contacts are traced a few days after the beginning of the epidemic, where almost all infections are treated and where people tend to protect themselves by wearing masks [8–10, 12]. However, this might overestimate the efficacy of the interventions in France, where pneumonic plague has never occurred, especially with an epidemic with a large number of index cases. The results obtained for the number of deaths in the reference scenario might, therefore, be underestimated.

The classical modelling we chose for travels between regions is frequently used in the literature [13, 14]. It tends to overestimate the size of the epidemic in all regions where the attack did not take place (e.g. people living in Paris who travel to stay in another region for sufficient time to become infectious there and then spread the epidemic in that region). In order to take into account the daily commuting of people working in a region different from where they live, we built a modified version of this model (results not shown), where all transports between regions were considered to be daily pendular commutes: every individual lives in a given region and goes daily to work in another region. This model produced similar results about the final size of the epidemic. Deaths were, however, more concentrated in Paris than in the model we present here. This corresponds to the fact that the majority of index cases become infectious in the seed region (Paris), and therefore do not really spread the epidemic in other regions.

Even if none of those models actually describes the nature of transports in France, a better approximation of the nature of transports between regions might be seen as a combination of travels and commutes: this combination would take into account the movements of working people returning home in the evening as well as the movements of tourists who stay longer in a region that they do not live. This model would reinforce the result that reducing transports between regions would help to concentrate the epidemic in the index area.

For the sake of simplicity, we assumed in our work that the whole population was homogeneous in a given regional area, a hypothesis which is probably unrealistic, since the confinement of patients to bed would probably concentrate the contacts in closed areas such as home and hospitals. The hypothesis of contact homogeneity was, however, made in most of the models which have been validated on bubonic or pneumonic plague [5, 15–17].

Furthermore, the value for R ₀ in our reference scenario was the only one we found in the literature [5]. It corresponds to frequent assumptions on the low contagiousness of pneumonic plague under normal situations [18–21]. High humidity of air can, however, be responsible for greater outbreaks with larger R ₀ values [9]. The method used by Gani & Leach to estimate this value took into account the number of secondary cases an infective produces, when the population was no longer fully susceptible [5]. The obtained value might rather be seen as an estimation of the parameter R, at the inception of the epidemic. Employing this method probably results in an underestimation of the true value of R ₀. As R ₀ belongs to the parameters which have a large influence on the predicted final size of the epidemic, results of the models realized on pneumonic plague should be interpreted with caution.