INTRODUCTION
The global prevalence of dengue has grown dramatically in recent decades. Currently it is estimated that some 2·5 billion people – two-fifths of the world's population – are at risk from dengue [1]. The disease is now endemic in more than 100 countries in Africa, the Americas, the Eastern Mediterranean, Southeast Asia and the Western Pacific regions. Southeast Asian and Western Pacific countries are among the most seriously affected.
Dengue outbreaks occur when there is a large fraction of susceptibles in a population living in an area where the dengue virus is circulating, and usually is preceded by a gradual localized build-up of Aedes mosquito density [Reference Gubler and Kuno2].
Some reasons have been proposed for the dramatic global emergence of dengue as a major public health problem: major global demographic changes have occurred, the most important of which have been uncontrolled urbanization and concurrent population growth; public health infrastructure of many of the affected countries has deteriorated; an increase in international travel provides an efficient mechanism for human transport of dengue viruses between urban centres, resulting in a frequent exchange of dengue viruses; and finally, effective mosquito control is virtually non-existent in many dengue-endemic countries [1].
Epidemiology of dengue in Singapore
In Singapore, dengue is endemic with year-round transmission [3]. The disease was first recognized as a public health problem in the 1960s when a nationwide Aedes control programme was implemented [Reference Goh4]. The programme basically integrated larval source reduction with measures inspired by public health education that consisted of instructing people on how to prevent breeding of Aedes mosquitoes within and outside residential premises. The programme was backed by law enforcement with heavy fines imposed on people whose premises were repeatedly found to have bred Aedes mosquitoes [3]. This programme resulted in a marked decline in dengue incidence, which coincided with a drop on the overall Aedes house index from over 25% to the present 1–2%. Despite the low Aedes house index (percentage of premises positive for Aedes breeding) outbreaks recurred from 1989 onwards with a discernible seasonal increase in the second half of each year [3].
Seroepidemiological surveys conducted in 1982–1984, 1990–1991, 1993 and 1998 indicated that dengue prevalence declined from 46% in 1982–1984 to 29·4% in 1998 [Reference Wilder-Smith5]. In spite of the great effort in Aedes control implemented in Singapore during the last decades, outbreaks had occurred with greater frequency and intensity with the largest outbreak reported in 2004–2005. The incidence of dengue increased from a baseline of 9·3 cases/100 000 inhabitants in 1988 to 312·2/100 000 in 2005. All four dengue serotypes have been detected, with DEN-3 predominating in 1992, DEN-2 in 1998 and DEN-1 in 2004–2005.
The 2004–2005 epidemic
A total of 13 817 dengue cases were reported in 2005 [6], peaking at 697 cases in the last week of September. The year 2005 exceeded all previous records of annual dengue incidence.
In terms of circulating virus strain, DEN-1 predominates even though DEN-3 has become more prevalent in the last months. Among cases, the male-to-female ratio was 1·4:1 with adults aged 15–44 years representing 65% of all reported cases. Unlike the epidemic of 1973 when children aged 5–14 years were the highest risk group, the highest age-specific incidence was in the 15–24 years age group while the lowest was in those aged <5 years. This suggests a predominance of extra-domiciliary infections [3].
Moreover, there has been an expansion in the geographical distribution of dengue outbreaks recently, from traditional landed areas in the eastern and south-eastern sectors of the island to new areas in the western and northern sectors where public housing estates are located (Fig. 1) [7]. Residents of those public housing estates represented 75% of reported dengue cases in 2004 and 2005 [3].

Fig. 1. Map of Singapore showing the 2005 dengue outbreak. ■, Aedes albopictus-infested area; ![]() , Aedes aegypti-infested area;
, Aedes aegypti-infested area; ![]() , dengue cases (from reference [7]).
, dengue cases (from reference [7]).
The model
Since the seminal attempts of Sir Ronald Ross in applying mathematics to understanding the transmission of malaria, several models to vector-borne infections have been proposed. In what follows we present a dynamical model for dengue transmission based on biological assumptions and on the available data of human cases [Reference Lopez8, Reference Coutinho9].
The model's dynamics are a modified version of the model from refs [Reference Coutinho9] and [Reference Coutinho10]. The structure, i.e. the number of compartments, transition rates, etc., is the same as the models presented in refs [Reference Coutinho9] and [Reference Coutinho10]. However, there is a very important difference. In the present paper, the average population of mosquitoes is allowed to increase slowly with time. This includes a new variable, which makes the present system non-autonomous in addition to the non-autonomous terms, simulating seasonality presented in the models in refs [Reference Coutinho9] and [Reference Coutinho10]. This is discussed in more details in equation (9) below.
Our model aims to compare the impact of several possible alternative control strategies, which in turn are based on the reproduction number of dengue fever, a threshold condition that will be described in the next section. It also aims to contribute to the understanding of the causes of dengue resurgence to Singapore in the last decade.
The popoulations involved in the transmission are human hosts, mosquitoes, and their eggs (the latter includes the intermediate stages, like larvae and pupae). The population densities, therefore, are divided in following compartments: susceptible humans, denoted S H; infected humans, I H; recovered (and immune) humans, R H; total humans, N H; susceptible mosquitoes, S M; infected and latent mosquitoes, L M; infected and infectious mosquitoes, I M; non-infected eggs, S E; and infected eggs, I E.
The model's equations are:

where c s(t)=(d 1−d 2 sin (2πft+φ)) is a climatic factor mimicking seasonal influences in the mosquito population (see below and references [Reference Coutinho9, Reference Coutinho10]). Those and the remaining parameters are explained in the Table.
Table. The parameters notation, biological meaning and values applied in the simulations

Let us briefly describe some features of the model.
Susceptible humans grow at the rate {r HN H[1−(N H/κH)]−μHS H}, where r H is the birth rate, μH is the natural mortality rate and κH is related to the human carrying capacity as explained below.
Humans are subject to a density-dependent birth rate and a linear mortality rate. The population dynamics in the absence of disease is
where r H is the birth rate of humans, N H is the total human population, k H is a constant and the human carrying capacity is [(r H−μH)/r H]κH.
Note that we are assuming that close to the carrying capacity the human population growth is checked by a reduction in the birth rate. Alternatively the control of the population could be done by a term including density dependence in the mortality rate and equation (2) could be written as
which can be interpreted as density dependence in the mortality rate. However, the net result would be qualitatively the same.
Those susceptible humans who acquire the infection do so at the rate [abI M(S H/N H)], where a is the average daily biting rates of mosquitoes and b H is the fraction of actually infective bites inflicted by infected mosquitoes, I M.
The second equation of model (1) describes infected humans, I H, who may either recover, with rate γ, or die from the disease, with rate (μH+αH).
The third equation of model (1) describes recovered humans, who remain recovered for the rest of their lives.
The fourth, fifth and the sixth equations of model (1) represent the susceptible, latent and infected mosquito population densities, respectively. Susceptible mosquitoes vary in size with a time-dependent rate
The term μM is the natural mortality rate of mosquitoes. The term p SS E is the number of eggs hatching per unit time, and which surviv the development through the intermediate stages (larvae and pupae). The term c S(t) simulates the seasonal variation in mosquito production from eggs (see below).
Those susceptible mosquitoes who acquire the infection do so at the rate [acS M(I H/N H)], where a is the average daily biting rates of mosquitoes and c is the fraction of bites inflicted by susceptible mosquitoes in infected humans that result in infected mosquitoes. Infected mosquitoes acquire the infection after biting infected humans with a rate [acS M(I H/N H)], spending some time in a latent period, called the extrinsic incubation period. The fraction of those latent mosquitoes that survive the extrinsic incubation period, with a given probability [exp (−μMτI)] become infective. Therefore, the rate of mosquitoes becoming infective per unit time is [exp (−μMτI)acS M(t−τI)(I H(t−τI)/N H(t−τI))].
The term p II E is the number of infected eggs hatching per unit time, and which survive the development through the intermediate stages (larvae and pupae).
The seventh and the eighth equations of model (1) represent the dynamics of susceptible and infected eggs, respectively.
In the seventh equation, the term
represent the oviposition rate of susceptible eggs born from both susceptible mosquitoes with rate
and from a fraction (1−g) of infected mosquitoes, with rate
The parameter g, therefore, represents the proportion of infected eggs laid by infected female mosquitoes.
The term r MS M represents the maximum oviposition rate of female mosquitoes with the number of viable eggs being checked by the availability of breeding places by the term {1−[(S E+I E)/κE]}. As in the case of humans, the egg carrying capacity is [(r E−μE)/r E]κE, where κE varies with time, as discussed and described below in equation (9). Once again we choose a density dependence on birth rather than on death. Again, the control of the population could be performed by a term including density dependence in the mortality rate, but the net result would be qualitatively the same.
Finally, in the last equation the term
represents the net rate by which infected eggs are produced by infected adult females, i.e. vertical transmission of dengue virus.
In the Appendix we present a derivation of a threshold condition and a sensitivity analysis.
The model's simulations
In the last 15 years the temperature in Singapore increased linearly [7]. This increase in temperature, in turn, is significantly correlated with the increase in the number of dengue cases (see Fig. 2).

Fig. 2. Correlation between the ambient temperature and dengue cases in the last 17 years (data from reference [7]).
We, therefore, assumed that this increase in the local temperature was responsible for an increase in the breeding conditions of Aedes mosquitoes, which can be simulated by a linear increase in the carrying capacity, κE such that:
To simulate seasonal variations in a schematic way we assumed:
where θ is the Heaviside function [Reference Lopez8]. The meaning of this substitution is that we assumed that the hatching rate of the eggs varies along the year being low in the ‘winter’ (low transmission season) and high in the ‘summer’ (high transmission season). To understand this, note that when d 1 is less than d 2, the θ function makes this rate vanish for a period during the ‘winter’. If d 2 is less than d 1 then the ‘winter’ is mild. When d 2=0 there is no seasonality. The term f is the frequency with which high and low transmission seasons alternate. Finally, the parameter φ is used to synchronize the population of mosquitoes so that it reaches a minimum when the hatching rate is also at minimum.
The result of the model's simulation for the 2004–2005 epidemic can be observed in Figure 3. We can see that the model tallies with the actual data with reasonable accuracy. Actually, we did not intend to fit the model to the data but rather reproduce qualitatively the trend in the number of cases observed in the last years. The parameter notation, biological meaning and values applied in the simulations are shown in the Table.

Fig. 3. Fitting accuracy of model (1) to real data for years 2003, 2004 and 2005 (data from http://www.moh.gov.sg/cmaweb/attachments/publication).
Simulating control
In October, 2005 the government implemented countrywide adulticidal and larvicidal control measures, which they called ‘carpet combing’. As a result of this intensive campaign, the number of cases dropped dramatically in the first weeks after the introduction of the control measures. Figure 4 shows the result of the campaign compared with the model projections if the control measures were not introduced.

Fig. 4. Simulation of the projected number of cases if the control programme was not introduced in October 2005, compared with real data (from http://www.moh.gov.sg/cmaweb/attachments/publication).
Note that, according to the model, after a seasonal fall in the number of cases the epidemic would bounce back to even higher levels.
Below we present a set of simulations aiming to analyse the impact of different control strategies. We simulate the reduction in the adult mosquito population by on-off fogging in different regimes, decreasing the adult mosquitoes lifespan by continued adulticide treatment, ‘search and destroy’ operations (larvicide treatment), which increase the eggs/immature stage mortality, the use of repellent by infective individuals, which we term ‘chemical quarantine’, and public education and law enforcement to achieve mosquitoes breeding source reduction, simulated by a reduction in egg-carrying capacity. We divide our simulations in two settings, continuous control and discontinuous control.
Continuous control
To simulate the adulticide control strategy, i.e. the use of insecticide by fogging machines thus killing adult mosquitoes, we increased the mosquitoes' mortality rate, μM. Analogously, larvicide strategy, that is removal and destruction of breeding habitats and killing immature forms of the mosquitoes by spreading chemical larvicide products in breeding places, was simulated by increasing the death mortality rates of immature stages, μE. Finally, the quarantine strategy, i.e. the use of substances that reduce the contact between infected humans and susceptible mosquitoes, such as repellents, was simulated by reducing the probability, c, of infective contact between infected humans and susceptible mosquitoes. The change in any of the above parameters means that the underlying control mechanisms were applied continuously in time. In the next section we shall consider a more realistic case where the control mechanisms are applied discontinuously, that is periodically interrupted such that the affected parameters return to their natural values.
Figure 5 shows the results for pure strategies at the level of 10%, i.e. increasing μM by 10% (adulticide), increasing μE by 10% (larvicide), and decreasing c by 10% (quarantine).

Fig. 5. Simulation of the impact of continuous pure strategies at the level of 10%, i.e. increasing mosquito mortality rate by 10% (adulticide; · · · · · · ·), increasing immature-stage mortality rate by 10% (larvicide; - - - -), and decreasing the probability of effective contagiousness between infected humans and mosquitoes by 10% (quarantine; ––––). Note that adulticide is the most effective strategy.
According to the sensitivity analysis (see Appendix), the most effective strategy is the sudden reduction in adult mosquitoes. The impact of killing adult mosquitoes is easily understood intuitively: the life expectancy of the mosquito is comparable with the extrinsic incubation period, so that increasing the mortality of adult mosquitoes sharply decreases the number of mosquitoes in the infective condition. This can be seen by examining the term [exp (−μMτI)] in model (1).
We also simulated mixed strategies, i.e. the combination of two or more of the above-mentioned pure strategies. Figure 6 illustrates the result of a mixed strategy that combines a 5% increase in mosquito mortality rate and a 10% increase in immature-stage mortality rate compared with the effect of each of the pure strategies described above.

Fig. 6. Simulation of the impact of a mixed strategy (––––) consisting of the combination of a 5% increase in mosquito mortality rate (· · · · · · · · ·) and a 10% increase in immature-stages mortality rate (- - - -) compared with pure strategies. Note that the combination is more effective than each pure strategy.
Note that the simulated mixed strategy reproduces, at least qualitatively, the dramatic reduction in dengue cases observed in the last 10 weeks. Again, we did not intend to fit the real data. Further, we are aware that there are infinite combinations of the possible strategies that could result in the same profile.
Discrete control
The simulations shown in the above session considered uninterrupted control, for example, the simulated increase in mosquito mortality was assumed as a continuous process that reduced mosquito survival by some fraction and that this process operated continuously in time. Obviously, such a strategy, although interesting from the theoretical point of view, is not feasible from the practical point of view. Therefore, it is more realistic to simulate a situation in which the control was applied discretely, that is, pulses of limited duration (1 day) every 5 weeks. In this process, the increase in mosquito mortality rate is represented by a square pulse function that acts for a short period of time and that can eventually be repeated several times at any given future moment. We simulated three pure strategies, namely, killing mosquitoes (reducing the mosquito population by 50%), killing immature stages (reducing egg population by 50%) and destroying breeding places (reducing the mosquitoes and immature stages carrying capacities by 50%), and a mixed strategy, which combines the three by performing them simultaneously.
The results of the pure-strategy simulations can be seen in Figure 7 in which the real data of the number of new cases is compared with each of the pure strategies. Note that none of the strategies if applied in isolation explain the real data.

Fig. 7. Simulation of six pulses of discrete control for three pure strategies, namely, reducing 50% of the mosquito population (· · · · · · · · ·), reducing 50% of immature stages (eggs, - - - -), and destroying breeding places by reducing the immature stages' carrying capacity by 50% (K S, –––), compared with no control (![]() ). Note that none of the strategies if applied in isolation explain the real data (◆).
). Note that none of the strategies if applied in isolation explain the real data (◆).
In Figure 8 we show the simulation of the mixed strategy, which combined the three pure strategies simultaneously, described above. It can be seen that the mixed strategy reproduces the descendent trend of actual data.

Fig. 8. Simulation of a mixed strategy combining the three strategies described in Figure 7. Note that this combination reproduces the actual descendent trend of the data.
Simulating the actual strategy implemented in Singapore
In 2005, the National Environmental Agency of Singapore, the agency responsible for vector control, adopted surveillance and ‘search and destroy’ breeding places as the main efforts in reducing the Aedes mosquito population. In addition, they have decided to reduce fogging. Fogging would be carried out only if field visits showed that there was an abundance of mosquitoes.
In October 2005, Singapore launched a nationwide campaign against dengue consisting of two key approaches, described below, called ‘Carpet Combing’ for outdoors and ‘10-Minute Mozzie Wipe-out’ for indoors. The ‘Carpet Combing’ exercise was conducted over a period of 6 weekends. More than 6000 volunteers from various government agencies and social organizations participated in ‘search and destroy’ operations. Some 1000 mosquito-breeding habitats were found and destroyed, and another 8400 potential breeding sites were removed.
The ‘10-Minute Mozzie Wipe-out’ initiative was a massive community outreach exercise to educate the public to check and remove stagnant water in homes. Some 10 000 volunteers spent their weekends distributing the ‘10-minute Mozzie Wipe-out’ pamphlet to about 880 000 homes to encourage residents to carry out a 10-minute mosquito prevention effort in their homes. The target groups included households, construction sites, shipyards, factories and foreign domestic workers.
In addition, an inter-agency dengue task force was formed in September 2005 to enhance the communication and coordination on dengue control efforts among various government agencies and private organizations. Since then, the mosquito control strategies of the various government agencies and private organizations have been strengthened. The agencies and private organizations undertook a thorough sweep of all their infrastructure, properties and development sites for which they were responsible. Permanent solutions to eliminate potential sources of stagnant water, e.g. repairs to infrastructure, sealing up of cracks, backfilling of land and removal of roof gutters were carried out.
We simulated the above strategy and the results can be seen in Figure 9. Note that this simulation reproduces the real data with good accuracy, including the recrudescence of dengue in the last weeks.

Fig. 9. Simulation of the actual control strategy applied in Singapore from October, 2005, compared to the real data (see text for a description of the strategy).
DISCUSSION
Mathematical models have proved to be useful tools in the understanding of dengue transmission and in helping the planning of control strategies [Reference Marques, Forattini and Massad11–Reference Ooi, Goh and Gubler14]. The current epidemic of dengue in Singapore is unprecedented and coincides with the increase in incidence of the disease observed in Southeast Asia [3].
A combination of several factors may have contributed to the resurgence of dengue in Singapore in the last years. Among the attributable variables for dengue resurgence are low level of herd immunity of the human population, re-emergence of one of the four circulating dengue serotypes, environmental factors, such as increase in temperature and precipitation; and demographic factors such as new cohorts of susceptibles and migratory movements in the country. However, it should be noted that the dengue control programme in Singapore is considered to be one of the best in the world and has resulted in sustained suppression of the Aedes aegypti vector for several years and it most unlikely that local public health authorities have relaxed such a programme.
Transmission persists in Singapore because the principal vector, A. aegypti, exists in the presence of a high human population density [3]. The role of other factors such as the importation of exotic strains has not been substantiated through genetic sequencing of the dengue viruses isolated.
There are some indications that environmental changes, as elsewhere in the world, were one of the key factors in determining the resurgence of dengue in Singapore. This, in addition to the increasing cohort of susceptibles seen in recent years should be enough to explain the observed number of new cases.
In this paper we choose to model the impact of environmental changes on dengue incidence by making the mosquito carrying capacity a state variable. This was based on the assumption that the increase in both the local average temperature observed in the last 15 years, and the number of new construction sites providing breeding places for mosquitoes, were monotonically increasing functions of time. We could have chosen to simulate the impact of environmental temperature on dengue transmission by acting on several parameters, e.g. the extrinsic incubation period (shortens with an increase in temperature), the biting rate, the hatching rate of eggs or the laying rate of eggs. However, by directly increasing the mosquitoes' carrying capacity we are simulating an increase in the total number of mosquitoes due to a higher number of breeding places favouring better egg-laying conditions.
A previous paper by Newton & Reiter [Reference Newton and Reiter15] showed that simulating ULV fogging (e.g. from an aeroplane) by a sudden reduction in the mosquito population without changing the mosquito mortality rate causes the population to fall and bounce back to pre-control levels in a few days. We simulated our model with Newton & Reiter's assumptions and reached the same result (see Fig. 10), although a single, very short and strong pulse of added mortality would produce indistinguishable results, as far as the mosquito population is concerned. The simulated impact on disease is consequently small (or negligible).

Fig. 10. Simulation of the model by Newton & Reiter [Reference Newton and Reiter15] showing that the impact on the number of mosquitoes by a single pulse of fogging is ephemeral.
However, public health authorities do not commonly consider a single pulse intervention. Therefore, we simulated continued intermittent fogging, e.g. at weekly frequency, which effectively reduces the mosquitoes' average lifespan for as long as the fogging continues and has, as we have seen, an appreciable impact on disease incidence.
From Newton & Reiter's model formulation, as mentioned above, the sudden reduction in mosquito population has little effect on dengue. This can be intuitively understood. As the turnover of mosquitoes is very high the mosquito population is restored within a few days, and would be quickly re-infected by the abundance of human cases, so that dengue transmission continues. A consistent reduction in mosquito lifespan, obtained by repeated fogging, is much more effective, at least from the theoretical point of view. The effect is nonlinear because the adult mosquito lifespan affects both the duration of infectiousness as well as the chances of survival to the infectious stage after completing the extrinsic incubation period; Newton & Reiter actually also show this effect in their table 4, where small changes in adult mosquito lifespan has an enormous impact on the peak human prevalence.
Newton & Reiter also show that, with constant fogging (four applications at 1-week intervals in their fig. 4), a similar result occurs to that predicted by our model – that is, there is a decrease in incidence, but there is a rebound once the fogging stops. In practical terms, it is worthwhile to point out that the abrupt reduction in adults from one-off fogging has far less (and almost negligible) effect compared to continued fogging. Newton & Reiter are in agreement with us that the intervention can impact the outbreak and thus buy time for other measures.
However, in our model we introduced seasonality on dengue transmission and as we demonstrated this has a major influence on outbreaks. We simulated our model with constant fogging (four applications at 1-week intervals) and demonstrate that, although the epidemic bounces back after interrupting control, this happens more than 1 year after interruption and to a significantly lower level (Fig. 11).

Fig. 11. Simulation of model (1) with the same condition as used by Newton & Reiter [Reference Newton and Reiter15] (four weekly fogging applications). Note that in our model the impact of this strategy is more durable.
This is a consequence of seasonality and of the fact that fogging would be most probably applied at the peak of human cases, which occurs in a moment when the mosquito population has already started to decline.
We are well aware of the logistic difficulties and the limited effectiveness of the application of adulticide methods under field conditions. However, our model shows that, at least from the theoretical point of view, killing mosquitoes is the most effective strategy in reducing dengue incidence at the peak of an outbreak. How to implement this may be a more difficult task than it seems at first sight but efforts should be made in order to circumvent the logistical aspects that currently limit the application of adulticide methods under field conditions.
APPENDIX
The threshold for transmission
A time-dependent threshold condition for transmission can be deduced from the model's equations [Reference Coutinho9, Reference Coutinho10] and results in the following equation:
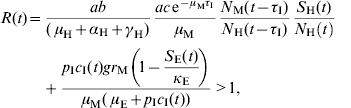
The first term of the equation, evaluated at t=0, is the Macdonald equation [Reference Macdonald16]. The second term comes from the model's terms related to immature stages as an important contributor for the epidemic.
In this work we simulated the impact on dengue outbreaks of four different control strategies, namely, killing adult mosquitoes (adulticide), killing immature stages (larvicide), preventing contact between infected humans and vectors (quarantine) and combinations of the first two (mixed).
The first strategy is implemented in the model by increasing the parameter μM, the mosquito mortality rate; the second strategy was simulated by increasing the parameter μE, the immature-stage mortality rate; the third strategy was simulated by reducing the product ac, i.e. by simulating a reduction in the contact between infected humans and susceptible vectors. Finally, the mixed strategies were simulated by a combination of the first two, i.e. by reducing μM and μE in different proportions.
Sensitivity analysis
In order to estimate the impact of alternative strategies we carried out a sensitivity analysis of the reproduction number to the following parameters: biting rate, the product of the parameters a and c, egg-carrying capacity, mosquito mortality rate, and immature-stage mortality rate. The choice of these parameters was related to the theoretical possibility of control. Therefore, the biting rate could be reduced by methods that avoid contact between humans and mosquitoes, e.g. bed nets, use of repellents, etc. The egg-carrying capacity can be reduced by the set of methods called ‘source reduction’, consisting of destroying breeding places. The mosquito mortality rate can be increased by the use of adulticide methods. Finally, the immature-stage mortality rate can be reduced by the application of larvicide methods.
The results are:
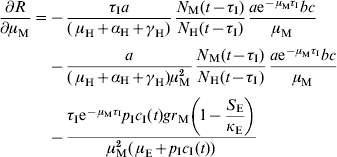
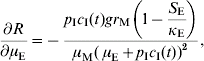
The parameter to which the model seems to be most sensitive is the daily mortality rate of adult mosquitoes. This was numerically confirmed.
ACKNOWLEDGEMENTS
This work was supported by LIM01/HCFMUSP, FAPESP, CNPq and the Courage Fund.
DECLARATION OF INTEREST
None.













