Simulation of the probable vector density that caused the Nagasaki dengue outbreak vectored by Aedes albopictus in 1942

Summary

Japan experienced dengue outbreaks vectored by Aedes albopictus during the Second World War. The probable vector density that caused the largest dengue outbreak in Nagasaki in 1942 was estimated using a mathematical simulation model. The estimated vector density was 15·0–558·0 per person when various assumptions of uncertain parameters were applied, such as proportion of symptomatic cases, vector mortality, and human biting rate of A. albopictus. When the most favourable disease spread conditions, such as a combination of the exclusive human biting rate and the longest vector survival were assumed, the vector density was 15–25 mosquitoes per person. Unusually high vector density due to wartime practices, and the traditional Japanese lifestyle were presumably responsible for the earlier dengue outbreak. If an outbreak occurs in present-day Japan, it is unlikely to spread as much as the previous one, as environmental conditions and human behaviour have changed in a protective manner.

INTRODUCTION

Dengue is one of the most serious mosquito-borne viral diseases, and major outbreaks have repeatedly occurred in the tropics and subtropics. Japan experienced dengue outbreaks during the Second World War; these outbreaks were recorded in southwestern Japan in the Kagoshima, Kumamoto, Nagasaki, Fukuoka, Hiroshima, Hyogo, Osaka and Mie prefectures [1, 2]. Of these, the largest outbreak was recorded in Nagasaki in 1942, in which 10% of the total population was reported to be symptomatic [3]. Although dengue is not a public health concern in Japan at present, annual mean temperature has gradually been increasing [4] and Aedes albopictus, the vector, has expanded its infestation range northwards [5] in recent decades. Millions of people now travel to Japan and other countries where dengue fever is endemic. Moreover, the number of imported dengue cases is on the rise [6], increasing the possibility of its re-emergence in Japan.

In mosquito-borne diseases, including dengue, the presence of the vector is necessary, but not sufficient, to cause epidemics. Outbreaks occur when vector density exceeds a certain transmission threshold, which is determined by factors such as ambient temperature and herd immunity level [7]. The Japanese population was considered naive to dengue prior to the outbreaks in the 1940s; the probable vector density that caused the outbreaks can be quantified based on the reported number of cases by simulating both the seasonal change in vector population and the effect of temperature on vector competence. Density is usually defined as quantity per unit measure, but we used the term differently; in this study, vector density indicates the number of female mosquitoes per person (MPP). MPP is an important indicator of the epidemic potential of dengue because the basic reproductive number (R ₀) is directly proportional to MPP in mosquito-borne diseases in cases where the biting rate of the vector is steady. R ₀ is defined as the expected number of secondary cases produced by the index case in a naive population during the entire period of infectiousness. When R ₀ ⩾ 1, transmission is maintained and spreads in the population; conversely R ₀ < 1 indicates that transmission declines and ceases.

It must be noted that A. albopictus was the principal vector in the 1940s outbreaks in Japan [3], whereas, Aedes aegypti is commonly the principal dengue vector in the tropics and subtropics. A. aegypti is highly domesticated and exhibits strong anthropophilia [8, 9]; the human biting rate (HBR; number of bites given to humans per cycle/expected number of bites per gonotrophic cycle) of this species is approximately 100%. Unlike A. aegypti, A. albopictus is relatively exophilic, feeding on various kinds of hosts [10]; finding and feeding on human hosts at every gonotrophic cycle is not easy for A. albopictus. It is likely that the HBR of A. albopictus is lower than that of A. aegypti, although the exact numbers are unknown.

Vector mortality is another important entomological parameter that influences the efficiency of viral transmission in mosquito-borne diseases [11]. However, the mortality rate of A. albopictus is not well understood. In previous studies, the reported average lifespan of A. albopictus varied widely from 2·7 to 20 days [10, 12].

The 1942 outbreak is considered the first dengue outbreak in Nagasaki; thus, all cases would be primary infections. Unfortunately, there is no serological data for the prevalence of anti-dengue antibodies in the population in Nagasaki. It is still unclear what proportion of infected individuals displayed clinical symptoms of dengue. Studies performed in areas where dengue is endemic and vectored principally by A. aegypti show that only a small proportion of primary infections are symptomatic; however, this can vary between 0 % and 70% [13, 14].

The importance of A. albopictus as a dengue vector is increasing because this species is currently the most invasive mosquito worldwide [15]. The presence of A. albopictus was first reported in 2004 in France and Croatia [16, 17], and just 6 years later, autochthonous dengue infections vectored by A. albopictus were reported in both countries [16, 18]. Thus, we believe that it is important to assess the vector competence of A. albopictus and estimate the number of female A. albopictus per person that caused a large dengue outbreak in the past. This may provide some perspectives towards reducing the dengue epidemic potential not only in Japan but also in those other temperate regions where A. albopictus can be the main source of dengue transmission.

In the present study, we aimed to estimate the probable vector density per person that caused the Nagasaki dengue outbreak in 1942 by using a mathematical model for dengue transmission dynamics based on the reported number of symptomatic cases. For uncertain parameters such as proportion of symptomatic cases, vector mortality rate, and HBR of A. albopictus, we applied various assumptions for the simulations.

METHODS

The model

We created a susceptible-exposed-infectious-recovered (SEIR) model of dengue virus transmission in a closed population; the equations are presented in Table 1. All parameters and their values are summarized in Table 2.

Table 1. Equations for the changes in each class of human and vector populations

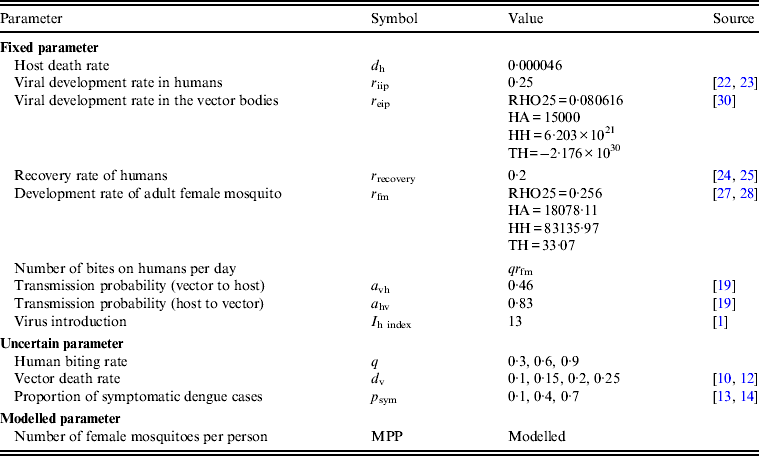
Table 2. Parameters and parameter values

RHO25, Development rate at 25°C; HA, enthalpy of activation of the reaction catalysed by the critical enzyme; HH, enthalpy change with high-temperature inactivation of the enzyme; TH, temperature at which 50% of the enzyme is inactivated.

Dengue virus

As our aim was to simulate the primary outbreak in a naive population, we employed only one dengue virus in our model. The virus was introduced into the population by the index case (I _{h_index}); I _{h_index} was assumed to be infectious on the day of arrival, and was not included in the resident population.

Transmission probabilities

Recent meta-analysis by Lambrechts et al. indicates that A. albopictus of ⩽5 generations in a laboratory colony possess a slightly higher oral receptivity of dengue virus (transmission probability from hosts to vectors: a _hv) [rate difference (RD) = 0·08] and a lower infectivity (transmission probability from vectors to hosts: a _vh) (RD=−0·29) than A. aegypti [19]. Applying these RD values on the generally accepted parameters for A. aegypti (0·75 for both a _hv and a _vh [20]), we derived 0·83 and 0·46 for a _hv and a _vh, respectively, for A. albopictus.

Host population

The population of Nagasaki (N _h) was 252 630 in 1940 [21]. We did not consider the distributions of age and sex. The host population was divided into S _h (susceptible), E _h (exposed), I _h (infectious), and R _h (recovered). We assumed that the entire population of Nagasaki was completely naive to dengue virus prior to its introduction; the initial values of S _h, E _h, I _h, and R _h were N _h, 0, 0, and 0, respectively.

Mortality rate of humans

Human life expectancy was arbitrarily set at 60 years. The daily mortality rate of humans (d _h) was 0·000046.

Viral development in the hosts

The intrinsic incubation period (IIP) was classically considered between 3–14 days (mean 5 days) [22]. Eighty percent of biting experiments from host to vector successfully transmitted the virus even a day before becoming symptomatic [23]. Hence, we adopted a constant value of 4 days for the IIP. The viral development rate in humans (r _iip) was set to a constant value of 0·25.

Recovery rate of the hosts

The infectious period in the host was considered between 2 and 10 days [22]. We assumed this value for 5 days in this model [24, 25]. The recovery rate of humans (r _recovery) was set to a constant value of 0·2.

Vector population

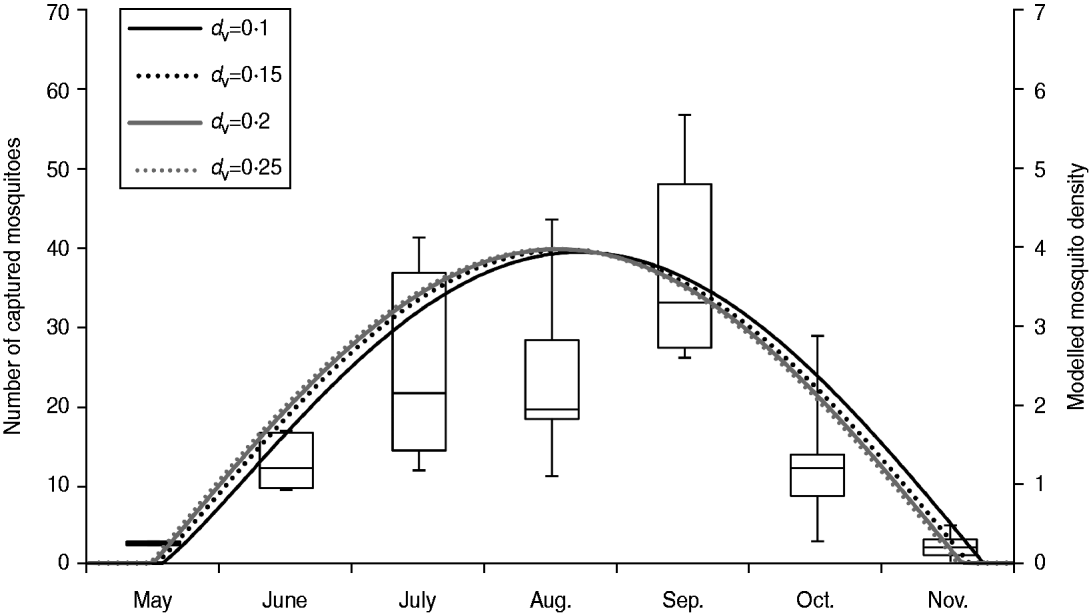
As male mosquitoes do not contribute to viral transmission, all the mosquitoes in our model were female mosquitoes. In Japan, the population of A. albopictus fluctuates seasonally and adult A. albopictus are usually found from May to November in Nagasaki [26]. Therefore, we assumed that mosquitoes were present only between 1 May (day 121) and 30 November (day 334) in our model. The peak mosquito population in a given year was determined by the product of the number of mosquitoes per person (MPP) and the human population (N _h). Seasonal mosquito population (N _v) on day t was mathematically modelled by a sinusoidal function as below, based on the field observation by Mori & Wada [26] (Fig. 1):

(1)$$\eqalign{\displaystyle{{dN_{\rm v}} \over {dt}}\tab = {\rm MPP}N_{\rm h} \sin \left[ {0.016882\left( {t + 240} \right)} \right]d_{\rm v} - N_{\rm v} d_{\rm v}\cr\tab \quad \quad \left( {121 \les t \les 334} \right),$$

where d _v is the vector mortality rate (see below).

Fig. 1. Seasonal changes in mosquito population. Left axis: box plot of monthly numbers of captured female A. albopictus during 1974–1976 in Nagasaki [26]. Right axis: seasonal changes in mosquito density [the number of female mosquitoes per person (MPP)] when the peak MPP = 4. d _v is the vector mortality rate. Note that the original data from Mori & Wada [26] consisted of the number of female mosquitoes captured during 30 and 15 min in 1974 and 1975–1976, respectively. The data from 1974 was therefore divided by two for representation in this figure.

The vector population was divided into S _v (susceptible), E _v (exposed), and I _v (infectious). Once infected, the vectors were assumed to possess lifelong infectivity. The initial value of S _v, E _v, and I _v was 0.

Developmental rate of the gonotrophic cycle of adult female mosquitoes

The length of the gonotrophic cycle was calculated based on the temperature-dependent enzyme kinetic model described in a previous study [27]. The developmental rate of adult female mosquitoes (r _fm) at temperature T (°C) was calculated by using the following equation:

(2)$$ r = \displaystyle{{{\rm RHO}25\left( {T\! +\! 273} \right)/298\rm exp [({\rm HA}/R) \cr \left\{ {(1/298) - 1/(T\! +\! 273)} \right\}]} \over {1 + \exp [({\rm HH}/R)\left\{ {1/({\rm TH} + 273) - 1/(T\! +\! 273)} \right\}]}}}$$

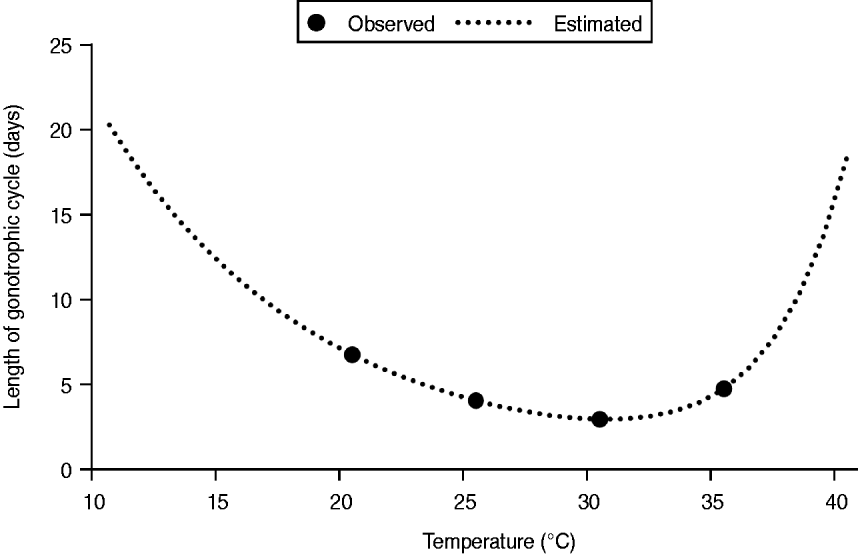
where, RHO25 is the development rate at 25°C without any temperature inactivation of the enzyme; HA (cal/mol) is the enthalpy of activation of the reaction that is catalysed by the critical enzyme; HH (cal/mol) is the enthalpy change with high-temperature inactivation of the enzyme; TH (°C) is the temperature at which 50% of the enzyme is inactivated at high temperature; R is the universal gas constant (1·987 cal/mol per degree). The values for RHO25, HA, HH, and TH for r _fm in A. albopictus were not provided in previous studies. On the basis of the observed length of the gonotrophic cycle of A. albopictus [28], we estimated the parameters for r _fm by using a curve-fitting method [29] (Fig. 2). The parameterized values of RHO25, HA, HH, and TH for r _fm are 0·256, 18078·11, 83135·97, and 33·07, respectively.

Fig. 2. Estimated length of the gonotrophic cycle using the curve-fitting method.

Viral development in the vectors

The extrinsic incubation period (EIP) is known to change seasonally as a function of temperature [30, 31]. We also applied equation (2) to calculate the temperature-dependent developmental rate of dengue virus in the vectors (r _eip). The EIP in A. albopictus is considered to be equivalent to that of A. aegypti based on recent meta-analysis [19]. Thus, parameters for r _eip were substituted with previously reported values for A. aegypti: RHO25 = 0·080616, HA = 15000, HH = 6·203 × 10²¹, TH=−2·176 × 10³⁰ [30].

Uncertain parameters

HBR

The HBR (q) is defined as the quotient of the number of successful blood meals on humans and the expected number of bites per gonotrophic cycle. A. albopictus usually consumes a single blood meal per cycle [32], hence, the expected number of bites should be 1. We set q at various levels for exclusive (0·9), moderate (0·6), and limited (0·3) biting, respectively. The daily number of bites given to humans per mosquito was determined by the length of gonotrophic cycle and the HBR, and calculated by qr _fm.

Mortality rate of adult mosquitoes

The mortality rate (d _v) of A. albopictus was set at various levels between 0·1 and 0·25 with increments of 0·05. The mortality of this species is relatively steady while ambient temperature is optimal for its survival [28], and it increases significantly at temperatures of <10°C or >35°C [33]. Thus, we assumed that d _v was constant at a range of 10–35°C, and that all mosquitoes will die within a day (d _v = 1) when the temperature is <10°C or >35°C.

Proportion of symptomatic dengue cases

The proportion of symptomatic cases (p _sym) was set at 0·1, 0·4, and 0·7. The daily incidence of symptomatic cases was calculated by the equation: p _symE _hr _iip.

Simulation

We obtained the recorded monthly temperatures of the city for 1942 [4] and converted them into daily values by interpolation. Precipitation, humidity, and diurnal length were assumed to be optimal to allow the survival and emergence of mosquitoes.

Estimation of the probable MPP

The time-course of the 1942 Nagasaki outbreak is well-documented [1]. It is reported that at least 13 dengue cases arrived at Nagasaki on 4 July. Subsequently, the first two domestic cases were recorded in a week, which rose to nine after a month. The reported cases increased to 2259 by the end of August, and further increased to 13323 by early October. In total, 23338 cases were recorded by the end of the year.

As reported, we conducted our simulation by introducing 13 infectious individuals (I _{h_index}) into the city on 4 July 1942. Simulations were initiated with MPP = 1·0. We changed MPP at increments of 0·1, and calculated the cumulative number of domestic symptomatic cases with various assumptions of q, d _v and p _sym until 31 December 1942. The likelihood of our estimates reflecting the reported cases was evaluated at 5 points by using the least squares method. The MPP that resulted in the best fit was defined as the probable MPP. We fitted the cumulative number of symptomatic cases for the simulation because of the limitation of data availability. As the Nagasaki outbreak occurred over 70 years ago during the war, daily, weekly, or monthly incidence was unavailable.

We also calculated R ₀ using the estimated MPP by the following R ₀ equation for dengue [34, 35]. As R ₀ is a point estimate, we representatively calculated R ₀ on the virus introduction day (4 July 1942) while ambient temperature was 24·3°C.

(3)$$R_0 = \displaystyle{{{\rm MPP}a_{{\rm vh}} a_{{\rm hv}} q^2 r_{{\rm fm}} ^2 r_{{\rm eip}} r_{{\rm iip}}} \over {\left( {r_{{\rm eip}} + d_{\rm v}} \right)d_{\rm v} \left( {r_{{\rm iip}} + d_{\rm h}} \right)\left( {r_{{\rm recovery}} + d_{\rm h}} \right)}},$$

Sensitivity analysis

To evaluate the impact of the parameters on our findings, we performed univariate, and multivariate sensitivity analyses by modifying the value of each parameter [36]. In univariate sensitivity analysis, the values of a _hv, a _vh, q, d _v, d _h, r _eip, r _iip, r _recovery, p _sym, and I _{h_index} were modified to increase by 1%, and the change in total number of cases was then calculated. In multivariate sensitivity analysis, these parameters were randomly sampled 1000 times at 25% above and below their baseline values. We obtained 1000 estimates of the cases followed by a multivariate linear regression analysis to investigate the parameters that most strongly affected the model. Significance was set at 0·01.

RESULTS

The probable MPP in the Nagasaki dengue outbreak in 1942 with various assumptions of q, d _v and p _sym are presented in Table 3.

Table 3. Probable number of Aedes albopictus per person during the Nagasaki dengue outbreak in 1942

When the exclusive HBR (q = 0·9) was assumed, the probable MPP was estimated as between 15·0 and 62·4. When the HBR was assumed to be moderate (q = 0·6), the higher probable MPP was estimated between 33·8 and 140·0. When the limited HBR (q = 0·3) was assumed, the estimated MPP was much higher, between 135·1 and 558·0.

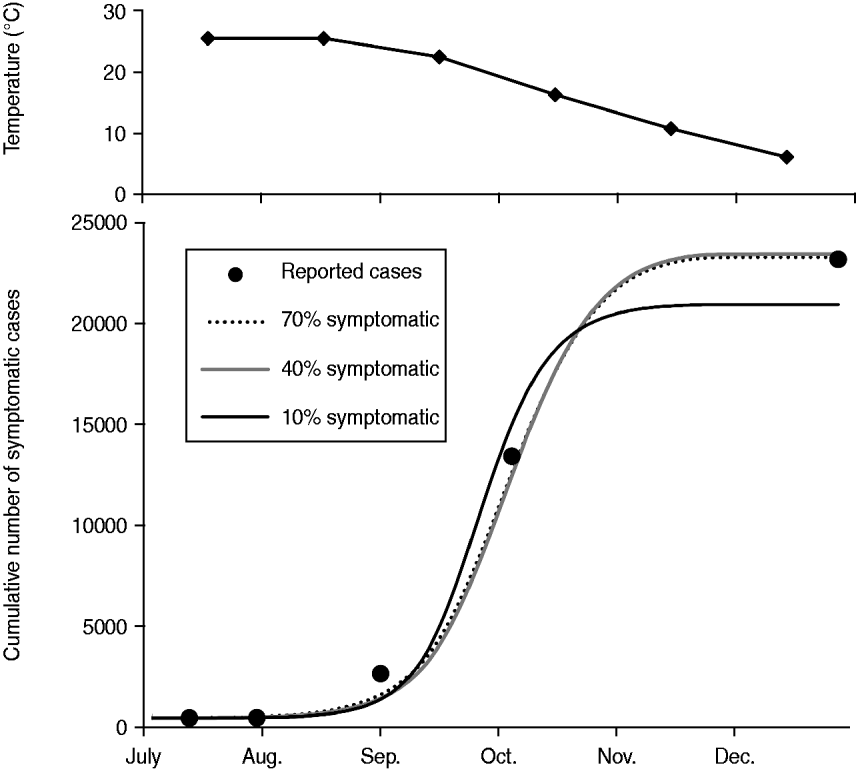
When the most favourable conditions for disease spread were assumed, such as a combination of the exclusive HBR (q = 0·9) and the longest vector survival (d _v = 0·1), MPPs of 15·0, 16·9, and 25·1 were required to cause the Nagasaki outbreak if 70%, 40%, and 10% of infected people were symptomatic, respectively (Fig. 3). When the most unfavourable conditions for disease spread were assumed, such as a combination of limited HBR (q = 0·3) and highest vector mortality (d _v = 0·25), the probable MPP appeared to be extremely high, i.e. 367·1, 405·2, and 558·0 at p _sym = 0·7, 0·4, and 0·1, respectively.

Fig. 3. Simulation results showing monthly mean temperature in Nagasaki in 1942 and the best fit simulations when the longest vector survival (d _v = 0·1), and the exclusive human biting rate (q = 0·9) are assumed. By using the least square method, the number of mosquitoes per person (MPP) was estimated to be 15·0, 16·9, and 25·1, while the proportion of symptomatic cases was assumed to be 0·7, 0·4, and 0·1, respectively.

Overall, the probable MPP increased with an increase in d _v, and it decreased with an increase in q and p _sym.

The estimated R ₀ values on 4 July are given in Table 4.

Table 4. Estimated R₀ during the Nagasaki dengue outbreak in 1942

Sensitivity analysis

The reference value for the total number of cases is 23445, which was estimated at q = 0·9, d _v = 0·1, and p _sym = 0·7, with MPP = 15·0. In the univariate sensitivity analysis, the parameter that most strongly affected the number of cases was q; there was a 10·1% increase with a 1% increase in q. The parameters with the subsequent strongest effects were a _vh and a _hv. The total number of cases increased by 4·9% with a 1% increase in a _vh and a _hv. This was followed by d _v, where the total number of cases decreased by 4·2% with a 1% increase in d _v. In the multivariate sensitivity analysis, the parameters that significantly affected total number of cases were q, a _hv, a _vh, d _v, r _eip, r _iip, and r _recovery.

DISCUSSION

In the present study, we attempted to estimate the probable number of A. albopictus per person that triggered the largest dengue outbreak in Japan, using a mathematical model that incorporated temperature-dependent developmental rate of the vector mosquito and dengue virus. We applied various assumptions for uncertain parameters such as the proportion of symptomatic cases, mortality rate, and the HBR of A. albopictus. Our results show that the probable MPP is a very high value between 15·0 and 558·0. When the most favourable condition for disease spread, such as a combination of the exclusive HBR and the longest vector survival was assumed, a MPP of at least 15–25 was required to cause the 1942 Nagasaki outbreak. A much higher MPP was required to trigger the outbreak if HBR was lower, and/or the vector lifespan was shorter. The trend showed that the probable MPP increased with increasing mortality rate, and decreasing HBR and proportion of symptomatic cases. The estimated R ₀ in the Nagasaki outbreak was between 6·1 and 13·9 in all settings.

The length of the gonotrophic cycle of A. albopictus was estimated to be 3–4 days between July and September by equation (2). Although the probable MPP was estimated to lie in a broad range, even a MPP of 15–25 appears to be a high density as this is almost equivalent to 4–8 mosquito bites per person per day if the HBR of mosquitoes is exclusive. The actual vector density during the 1942 Nagasaki outbreak is unknown, but it must have been very high as described in a report of the time in the following manner: ‘Aedes albopictus was dancing everywhere and an uncountable number of larvae was found in the outside water tanks’ [3]. Since Japan was at war in 1942, large numbers of water tanks were located around the houses for preventing fires resulting from bombings, and the tanks were considered as important mosquito breeding sites [2]. Presumably, this extremely high vector density was the most critical causal factor of the Nagasaki outbreak. In addition, most of the houses did not have window screens, and windows were usually left open for ventilation in summer which provided the mosquitoes with easy access to the houses. People tended to go outside to enjoy the cool breeze in the evening, allowing A. albopictus to easily consume a blood meal on humans [10]. The traditional Japanese lifestyle and human behaviour were likely to increase the frequency of mosquito–human contacts in and around the houses. The HBR of A. albopictus at that time could be assumed to be almost as high as that of A. aegypti. As our result indicated, the required mosquito density to cause the Nagasaki outbreak was estimated unrealistically high at more than 100–500 mosquitoes per person, if the limited HBR (q = 0·3) was assumed in the simulation (Table 3).

In present-day Japan, such water tanks no longer exist, but a new problem has arisen with regard to potential mosquito breeding sources in urban and suburban areas. There are several catch basins at the bottom of rainwater drainage systems around houses. These catch basins maintain rainwater for several days or weeks following rain, and have recently been implicated as one of the main sources for mosquito breeding. Although A. albopictus is known to be an omnivorous mosquito, it exhibits a relatively high anthropophilic feeding pattern in urban and suburban areas in Japan [37]. Therefore, this is an important problem in the context of public health because a high vector abundance in residential areas with a high density of susceptible hosts is clearly undesirable for the prevention of mosquito-borne diseases.

Although a higher vector density can be observed focally where breeding sources are particularly abundant, we believe that the current density of A. albopictus is significantly less than the extremely high density described in the earlier report. On average, a Japanese individual is bitten less than once a day by A. albopictus (data not shown). Most Japanese houses and buildings now have an airtight structure with intact window screens; such structural features help prevent the entry of A. albopictus [38]. Nearly 90% of households contain air conditioners [39], and people tend to stay indoors during the summer. Additionally, several effective repellents and insecticides are available in the market and many people use repellents both indoors and outdoors. We expect that such changes in the living environment, coupled with human behaviour would considerably decrease contact frequency with mosquitoes, regardless of density [40].

However, we could not directly compare the vector densities between the earlier outbreak and the present, since the actual density of A. albopictus in the natural environment still remains unknown. Although conducting entomological field surveillance is beyond the scope of this study, it is one of the study's limitations; it is important to investigate if the vector density in present-day Japan is definitively lower than the threshold for the prevention of the re-emergence of dengue.

Several studies attempted to estimate R ₀ values in dengue outbreaks in areas where dengue is vectored by A. aegypti. R ₀ was estimated as 2·0–103 in Brazil [41], 0·49–3·30 in Mexico [42], 1·89–2·23 in Singapore [43], and 3·93–4·67 in Taiwan [44]. Our estimated R ₀ (6·1–13·9) was relatively high but compatible with these values. Nishiura indicated that the proportion of asymptomatic cases should be taken into consideration in the estimation of R ₀ [45], and our result revealed that R ₀ was higher when the majority of infected individuals were asymptomatic (Table 4).

Our study has a number of other limitations. First, due to the deterministic nature of our model, stochastic phenomena involved in the real world transmission dynamics could not be depicted in this study.

Second, the presence of A. albopictus was determined based on seasonality in this model (Fig. 1). We incorporated the effects of ambient temperature on the development and survival of mosquitoes; however, various seasonal climatic factors other than temperature also influence mosquito population dynamics in nature. Precipitation determines breeding site availability, and diurnal length induces egg diapause [46]. These factors were assumed to be optimal for emergence and survival of the vector in this model. However, if the effects of these climatic factors were additionally incorporated, they may affect our findings since seasonal mosquito population fluctuations are more complex.

Third, we assumed a slightly lower viral transmissibility of A. albopictus in this model on the basis of a recent meta-analysis [19]; however, the vector competence of A. albopictus, and its comparison with that of A. aegypti is debatable [47–49]. As shown by our sensitivity analysis, if the actual values of transmission probability (a _vh and a _hv) are very different from our assumption, it strongly affects the value of the probable vector densities.

Fourth, we assumed a constant mortality rate of mosquitoes within a viable temperature range (10–35°C), with the rate markedly increasing when the temperature was out of range. The optimal temperature for mosquito survival is believed to be between 15°C and 30°C [28]. The effect of temperatures in the range of 10–14°C, and 31–35°C on mortality rate is uncertain. If the mortality rate increases at these suboptimal temperatures, our assumption may be overly simplistic to describe the actual survival ability of mosquitoes.

Fifth, our model does not include spatial heterogeneity of vectors and hosts. According to the 20–80 rule in vector-borne diseases, 20% of the host population is responsible for 80% of net transmission [50]. In fact, it has been reported that 70–75% of reported dengue cases occur in limited areas where vector mosquitoes are abundant, and/or several susceptible hosts are clustered together [51, 52]. However, we assumed that the transmission takes place homogeneously in the entire population in this model.

Despite these limitations, our study highlights that the unusually high vector density due to wartime practices and the traditional Japanese lifestyle were principally responsible for the Nagasaki dengue outbreak in 1942. We do not deny the possibility of re-emergence of dengue outbreaks in present-day Japan, since A. albopictus is still abundant. However, in the event of a recurrence, it is likely that the outbreak will remain focal and not spread as much as the earlier one, since circumstances have changed leading to a modern lifestyle and protective human behaviour.

Finally, we emphasize that there are still several entomological uncertainties with A. albopictus as a dengue vector. Future research is required to evaluate the risk of the diseases such as dengue and chikungunya that are transmitted by this species in Japan and other countries where A. albopictus is present, but epidemics have not yet occurred.