Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T16:17:59.721Z Has data issue: false hasContentIssue false
  • English
  • Français

2-chains and square roots of Thompson’s group $F$

Part of: PL-topology Low-dimensional dynamical systems Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  25 March 2019

THOMAS KOBERDA Open the ORCID record for THOMAS KOBERDA [Opens in a new window]  and
YASH LODHA
THOMAS KOBERDA
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA22904-4137, USA email thomas.koberda@gmail.com
YASH LODHA
Affiliation:
EPFL SB MATH EGG, Station 8, MA C3 584 (Bâtiment MA), Station 8, CH-1015, Lausanne, Switzerland email yash.lodha@epfl.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

We study 2-generated subgroups 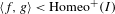$\langle f,g\rangle <\operatorname{Homeo}^{+}(I)$ such that 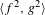$\langle f^{2},g^{2}\rangle$ is isomorphic to Thompson’s group $F$, and such that the supports of 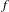$f$ and $g$ form a chain of two intervals. We show that this class contains uncountably many isomorphism types. These include examples with non-abelian free subgroups, examples which do not admit faithful actions by 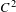$C^{2}$ diffeomorphisms on 1-manifolds, examples which do not admit faithful actions by 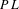$PL$ homeomorphisms on an interval, and examples which are not finitely presented. We thus answer questions due to Brin. We also show that many relatively uncomplicated groups of homeomorphisms can have very complicated square roots, thus establishing the behavior of square roots of $F$ as part of a general phenomenon among subgroups of 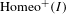$\operatorname{Homeo}^{+}(I)$.

Keywords

Thompson’s grouporderable groupequations over homeomorphism groupssmoothable group actions

MSC classification

Primary: 57M60: Group actions in low dimensions
Secondary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth) 57Q99: None of the above, but in this section 57S25: Groups acting on specific manifolds 20F60: Ordered groups 20F14: Derived series, central series, and generalizations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2515 - 2532
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergman, G. M.. Ordering coproducts of groups and semigroups. J. Algebra 133(2) (1990), 313–339.Google Scholar
Bieri, R. and Strebel, R.. On Groups of PL-Homeomorphisms of the Real Line (Mathematical Surveys and Monographs, 215). American Mathematical Society, Providence, RI, 2016.Google Scholar
Bleak, C., Brin, M. G., Kassabov, M., Moore, J. T. and Zaremsky, M. C.B.. Groups of fast homeomorphisms of the interval. J. Combin. Algebra. 3(1) (2019), 1–40.Google Scholar
Bludov, V. V. and Glass, A. M. W.. On free products of right ordered groups with amalgamated subgroups. Math. Proc. Cambridge Philos. Soc. 146(3) (2009), 591–601.Google Scholar
Brin, M. G.. The ubiquity of Thompson’s group F in groups of piecewise linear homeomorphisms of the unit interval. J. Lond. Math. Soc. (2) 60(2) (1999), 449–460.Google Scholar
Brin, M. G.. Personal communication, 2008.Google Scholar
Brin, M. G. and Squier, C. C.. Groups of piecewise linear homeomorphisms of the real line. Invent. Math. 79(3) (1985), 485–498.Google Scholar
Brown, K. S.. Finiteness properties of groups. Proceedings of the Northwestern Conference on Cohomology of Groups, Vol. 44 (Evanston, Ill., 1985). North-Holland, Amsterdam, 1987, pp. 45–75.Google Scholar
Brown, K. S. and Geoghegan, R.. An infinite-dimensional torsion-free FP∞ group. Invent. Math. 77(2) (1984), 367–381.Google Scholar
Burillo, J.. Thompson’s Group F. 2016.Google Scholar
Calegari, D.. Foliations and the Geometry of 3-Manifolds (Oxford Mathematical Monographs). Oxford University Press, Oxford, 2007.Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R.. Introductory notes on Richard Thompson’s groups. Enseign. Math. (2) 42(3–4) (1996), 215–256.Google Scholar
de la Harpe, P.. Topics in Geometric Group Theory (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, 2000.Google Scholar
Dehornoy, P., Dynnikov, I., Rolfsen, D. and Wiest, B.. Ordering Braids (Mathematical Surveys and Monographs, 148). American Mathematical Society, Providence, RI, 2008.Google Scholar
Deroin, B., Navas, A. and Rivas, C.. Groups, Orders, and Dynamics. 2019, to appear.Google Scholar
Farb, B. and Franks, J.. Groups of homeomorphisms of one-manifolds. III. Nilpotent subgroups. Ergod. Th. & Dynam. Sys. 23(5) (2003), 1467–1484.Google Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton Mathematical Series, 49). Princeton University Press, Princeton, NJ, 2012.Google Scholar
Ghys, É.. Groups acting on the circle. Enseign. Math. (2) 47(3–4) (2001), 329–407.Google Scholar
Ghys, É. and Sergiescu, V.. Sur un groupe remarquable de difféomorphismes du cercle. Comment. Math. Helv. 62(2) (1987), 185–239.Google Scholar
Higman, G.. On infinite simple permutation groups. Publ. Math. Debrecen 3 (1955), 221–226.Google Scholar
Higman, G.. Finitely presented infinite simple groups. Notes on Pure Mathematics, No. 8, Department of Pure Mathematics, Department of Mathematics, I.A.S. Australian National University, Canberra, 1974.Google Scholar
Kim, S.-H., Koberda, T. and Lodha, Y.. Chain groups of homeomorphisms of the interval. Ann. Sci. Éc. Norm. Supér., to appear.Google Scholar
Lyndon, R. C. and Schupp, P. E.. Combinatorial Group Theory (Classics in Mathematics). Springer, Berlin, 2001. Reprint of the 1977 edition.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics), Spanish edn. University of Chicago Press, Chicago, 2011.Google Scholar
Plante, J. F. and Thurston, W. P.. Polynomial growth in holonomy groups of foliations. Comment. Math. Helv. 51(4) (1976), 567–584.Google Scholar
Serre, J.-P.. Trees (Springer Monographs in Mathematics). Springer, Berlin, 2003. Translated from the French original by John Stillwell, Corrected 2nd printing of the 1980 English translation.Google Scholar