Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T20:46:52.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Accessibility and centralizers for partially hyperbolic flows

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  11 May 2021

TODD FISHER  and
BORIS HASSELBLATT
TODD FISHER*
Affiliation:
Department of Mathematics, Brigham Young University, Provo, UT84602, USA
BORIS HASSELBLATT
Affiliation:
Department of Mathematics, Tufts University, Medford, MA02144, USA (e-mail: boris.hasselblatt@tufts.edu)
*
e-mail: tfisher@math.byu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Stable accessibility of partially hyperbolic systems is central to their stable ergodicity, and we establish its 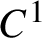$C^1$ -density among partially hyperbolic flows, as well as in the categories of volume-preserving, symplectic, and contact partially hyperbolic flows. As applications, we obtain on one hand in each of these four categories of flows the 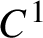$C^1$ -density of the 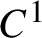$C^1$ -stable topological transitivity and triviality of the centralizer, and on the other hand the 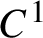$C^1$ -density of the 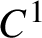$C^1$ -stable K-property of the natural volume in the latter three categories.

Keywords

accessibilitycentralizerdynamical systemspartially hyperbolic systems and dominated splittings

MSC classification

Primary: 37C80: Symmetries, equivariant dynamical systems
Secondary: 37D30: Partially hyperbolic systems and dominated splittings 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 3: Anatole Katok Memorial Issue Part 2: Special Issue of Ergodic Theory and Dynamical Systems , March 2022 , pp. 835 - 854
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

To the memory of Anatole Katok

References

Arbieto, A. and Matheus, C.. A pasting lemma and some applications for conservative systems. Ergod. Th. & Dynam. Sys. 27(5) (2007), 1399–1417, with an appendix by Diica, D. and Simpson-Weller, Y..CrossRefGoogle Scholar
Arnaud, M.-C.. Le “closing lemma” en topologie ${C}^1$ . Mém. Soc. Math. Fr. (N.S.) 74 (1998), vi+120.Google Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. Symplectomorphisms with positive metric entropy. Preprint, 2019, arXiv:1904.01045.Google Scholar
Bakker, L., Fisher, T. and Hasselblatt, B.. Centralizers of hyperbolic and kinematic-expansive flows. Preprint, 2019, arXiv:1903.10948.Google Scholar
Barthelmé, T. and Gogolev, A.. Centralizers of partially hyperbolic diffeomorphisms in dimension 3. Preprint, 2019, arXiv:1911.05532.Google Scholar
Bonatti, C., Crovisier, S. and Wilkinson, A.. The ${C}^1$ generic diffeomorphism has trivial centralizer. Publ. Math. Inst. Hautes Études Sci. 109 (2009), 185–244.CrossRefGoogle Scholar
Bonomo, W., Rocha, J. and Varandas, P.. The centralizer of Komuro-expansive flows and expansive ${\mathbb{R}}^d$ actions. Math. Z. 289(3–4) (2018), 1059–1088.CrossRefGoogle Scholar
Bonomo, W. and Varandas, P.. ${C}^1$ -generic sectional Axiom A flows have only trivial symmetries. Port. Math. 76(1) (2019), 29–48.CrossRefGoogle Scholar
Bonomo, W. and Varandas, P.. A criterion for the triviality of the centralizer for vector fields and applications. J. Differential Equations 267(3) (2019), 1748–1766.CrossRefGoogle Scholar
Brin, M. I.. Topological transitivity of a certain class of dynamical systems, and flows of frames on manifolds of negative curvature. Funktsional. Anal. i Prilozhen. 9(1) (1975), 9–19.CrossRefGoogle Scholar
Brin, M. I. and Pesin, Ya. B.. Partially hyperbolic dynamical systems. Uspekhi Mat. Nauk 28(3(171)) (1973), 169–170.Google Scholar
Brin, M. I. and Pesin, Ya. B.. Partially hyperbolic dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 170–212.Google Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171 (1) (2010), 451–489.CrossRefGoogle Scholar
Burslem, L.. Centralizers of partially hyperbolic diffeomorphisms. Ergod. Th. & Dynam. Sys. 24 (1) (2004), 55–87.CrossRefGoogle Scholar
Catsigeras, E. and Tian, X.. Dominated splitting, partial hyperbolicity and positive entropy. Discrete Contin. Dyn. Syst. 36 (9) (2016), 4739–4759.CrossRefGoogle Scholar
Damjanovic, D., Wilkinson, A. and Xu, D.. Pathology and asymmetry: centralizer rigidity for partially hyperbolic diffeomorphisms. Preprint, 2019, arXiv:1902.05201.Google Scholar
Damjanovic, D. and Xu, D.. On classification of higher rank Anosov actions on compact manifold. Israel J. Math. 238(2) (2020), 745–806.CrossRefGoogle Scholar
Dolgopyat, D. and Wilkinson, A.. Stable accessibility is ${C}^1$ dense. Astérisque 287 (2003), 33–60, Geometric methods in dynamics. II.Google Scholar
Fisher, T. and Hasselblatt, B.. Hyperbolic Flows (Zürich Lectures in Advanced Mathematics). European Mathematical Society (EMS), Zürich, 2020.Google Scholar
Foulon, P. and Hasselblatt, B.. Contact Anosov flows on hyperbolic 3-manifolds. Geom. Topol. 17 (2) (2013), 1225–1252.CrossRefGoogle Scholar
Foulon, P., Hasselblatt, B. and Vaugon, A.. Orbit growth of contact structures after surgery. Ann. H. Lebesgue, 2020, to appear.CrossRefGoogle Scholar
Gan, S., Shi, Y., Xu, D. and Zhang, J.. Centralizers of derived-from-Anosov systems on ${T}^3$ : rigidity versus triviality. Preprint, 2020, arXiv:2006.00450.CrossRefGoogle Scholar
Geiges, H.. An Introduction to Contact Topology (Cambridge Studies in Advanced Mathematics, 109). Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Grayson, M., Pugh, C. and Shub, M.. Stably ergodic diffeomorphisms. Ann. of Math. (2) 140(2) (1994), 295–329.CrossRefGoogle Scholar
Katok, A. B. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995, With a supplementary chapter by Katok and L. Mendoza.CrossRefGoogle Scholar
Katok, A. B. and Spatzier, R. J.. Differential rigidity of Anosov actions of higher rank abelian groups and algebraic lattice actions. Tr. Mat. Inst. Steklova 216(Din. Sist. i Smezhnye Vopr.) (1997), 292–319.Google Scholar
Leguil, M., Obata, D. and Santiago, B.. On the centralizer of vector fields: criteria of triviality and genericity results. Math. Z. 297 (2021), 283–337.CrossRefGoogle Scholar
Obata, D.. Symmetries of vector fields: the diffeomorphism centralizer. Preprint, 2019, arXiv:1903.05883.Google Scholar
Oka, M.. Expansive flows and their centralizers. Nagoya Math. J. 64 (1976), 1–15.CrossRefGoogle Scholar
Pesin, Ya. B.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics). European Mathematical Society (EMS), Zürich, 2004.CrossRefGoogle Scholar
Pugh, C. and Shub, M.. Stable ergodicity and julienne quasi-conformality. J. Eur. Math. Soc. (JEMS) 2(1) (2000), 1–52.CrossRefGoogle Scholar
Pugh, C. and Shub, M.. Stable ergodicity. Bull. Amer. Math. Soc. (N.S.) 41(1) (2004), 1–41, with an appendix by A. Starkov.CrossRefGoogle Scholar
Pugh, C., Shub, M. and Starkov, A.. Corrigendum to: Stable ergodicity and julienne quasi-conformality [J. Eur. Math. Soc. (JEMS) 2(1) (2000), 1–52]. J. Eur. Math. Soc. (JEMS) 6(1) (2004), 149–151.CrossRefGoogle Scholar
Sad, P. R.. Centralizers of vector fields. Topology 18(2) (1979), 97–104.CrossRefGoogle Scholar
Teixeira, P.. On the conservative pasting lemma. Ergod. Th. & Dynam. Sys. 40(5) (2020), 1402–1440.CrossRefGoogle Scholar