Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jones, Roger L.
1992.
A remark on singular integrals with complex homogeneity.
Proceedings of the American Mathematical Society,
Vol. 114,
Issue. 3,
p.
763.
Jones, Roger L.
Ostrovskii, Iosif V.
and
Rosenblatt, Joseph M.
1996.
Square functions in ergodic theory.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
267.
Akcoglu, Mustafa
Bellow, Alexandra
Jones, Roger L.
Losert, Viktor
Reinhold-Larsson, Karin
and
Wierdl, Máté
1996.
The strong sweeping out property for lacunary sequences, Riemann sums, convolution powers, and related matters.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
207.
Junco, Andrés del
2009.
Encyclopedia of Complexity and Systems Science.
p.
2933.
del Junco, Andrés
2009.
Ergodic Theory.
p.
79.
Reinhold, Karin
Savvopoulou, Anna K.
and
Wedrychowicz, Christopher M.
2012.
Almost Everywhere Convergence of Convolution Measures.
Canadian Mathematical Bulletin,
Vol. 55,
Issue. 4,
p.
830.
Junco, Andrés del
2012.
Mathematics of Complexity and Dynamical Systems.
p.
241.
Conze, Jean-Pierre
and
Lin, Michael
2013.
Almost everywhere convergence of convolution powers on compact Abelian groups.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 49,
Issue. 2,
Chistyakov, G. P.
2013.
Limit Theorems in Probability, Statistics and Number Theory.
Vol. 42,
Issue. ,
p.
75.
Cohen, Guy
Cuny, Christophe
and
Lin, Michael
2014.
Almost everywhere convergence of powers of some positiveLpcontractions.
Journal of Mathematical Analysis and Applications,
Vol. 420,
Issue. 2,
p.
1129.
Das, Suddhasattwa
Saiki, Yoshitaka
Sander, Evelyn
and
Yorke, James A.
2016.
The Foundations of Chaos Revisited: From Poincaré to Recent Advancements.
p.
103.
Tempelman, Arkady
and
Shulman, Alexander
2019.
Dominated and pointwise ergodic theorems with “weighted” averages for bounded Lamperti representations of amenable groups.
Journal of Mathematical Analysis and Applications,
Vol. 474,
Issue. 1,
p.
23.

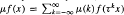 for all
for all 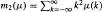 finite and
finite and 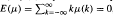 then for all
then for all 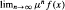 exists for a.e.
exists for a.e. 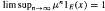 a.e. and
a.e. and 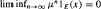 a.e. In the case when
a.e. In the case when 