Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-29T21:47:43.123Z Has data issue: false hasContentIssue false
  • English
  • Français

Aperiodicity at the boundary of chaos

Published online by Cambridge University Press:  04 May 2017

STEVEN HURDER  and
ANA RECHTMAN
STEVEN HURDER
Affiliation:
Department of Mathematics, University of Illinois at Chicago, 322 SEO (m/c 249), 851 S. Morgan Street, Chicago, IL 60607-7045, USA email hurder@uic.edu
ANA RECHTMAN
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 Ciudad de México, México email rechtman@im.unam.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the dynamical properties of 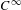$C^{\infty }$-variations of the flow on an aperiodic Kuperberg plug $\mathbb{K}$. Our main result is that there exists a smooth one-parameter family of plugs 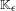$\mathbb{K}_{\unicode[STIX]{x1D716}}$ for 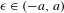$\unicode[STIX]{x1D716}\in (-a,a)$ and 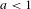$a<1$, such that: (1) the plug 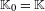$\mathbb{K}_{0}=\mathbb{K}$ is a generic Kuperberg plug; (2) for 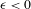$\unicode[STIX]{x1D716}<0$, the flow in the plug 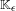$\mathbb{K}_{\unicode[STIX]{x1D716}}$ has two periodic orbits that bound an invariant cylinder, all other orbits of the flow are wandering, and the flow has topological entropy zero; (3) for $\unicode[STIX]{x1D716}>0$, the flow in the plug 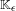$\mathbb{K}_{\unicode[STIX]{x1D716}}$ has positive topological entropy, and an abundance of periodic orbits.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2683 - 2728
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Edwards, R., Millett, K. and Sullivan, D.. Foliations with all leaves compact. Topology 16 (1977), 13–32.Google Scholar
Epstein, D. B. A. and Vogt, E.. A counterexample to the periodic orbit conjecture in codimension 3. Ann. of Math. (2) 108 (1978), 539–552.Google Scholar
Ghys, É.. Construction de champs de vecteurs sans orbite périodique (d’après Krystyna Kuperberg), Séminaire Bourbaki, Vol. 1993/94, Exp. No. 785. Astérisque 227 (1995), 283–307.Google Scholar
Hurder, S. and Rechtman, A.. The dynamics of generic Kuperberg flows. Astérisque 377 (2016), 1–250.Google Scholar
Hurder, S. and Rechtman, A.. Perspectives on Kuperberg flows. Preprint, 2016, arXiv:1607.00731, submitted.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.Google Scholar
Kuperberg, K.. A smooth counterexample to the Seifert conjecture. Ann. of Math. (2) 140 (1994), 723–732.Google Scholar
Kuperberg, G. and Kuperberg, K.. Generalized counterexamples to the Seifert conjecture. Ann. of Math. (2) 144 (1996), 239–268.Google Scholar
Matsumoto, S.. K. M. Kuperberg’s C ∞ counterexample to the Seifert conjecture. Sūgaku, Math. Soc. Japan 47 (1995), 38–45; Translation: Sugaku expositions, Amer. Math. Soc. 11, (1998) 39–49.Google Scholar
Matsumoto, S.. The unique ergodicity of equicontinuous laminations. Hokkaido Math. J. 39 (2010), 389–403.Google Scholar
Sullivan, D.. A counterexample to the periodic orbit conjecture. Publ. Math. Inst. Hautes Études Sci. 46 (1976), 5–14.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Wilson, F. W. Jr. On the minimal sets of non-singular vector fields. Ann. of Math. (2) 84 (1966), 529–536.Google Scholar