Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mastrangelo, Laura
Muhly, Paul S.
and
Solel, Baruch
1994.
Locating the radical of a triangular operator algebra.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 1,
p.
27.
Muhly, Paul S.
and
Solel, Baruch
1996.
Representations of triangular subalgebras of groupoid C*-algebras.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 61,
Issue. 3,
p.
289.
Shpigel, Miron
1999.
The ideal structure of some analytic crossed products.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 6,
p.
2515.
Katsoulis, Elias G.
and
Ramsey, Christopher
2016.
Limit algebras and integer-valued cocycles, revisited.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 3,
p.
839.

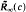 , is an invariant for the total order
, is an invariant for the total order 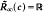 if and only if the analytic algebra has a certain maximality property.
if and only if the analytic algebra has a certain maximality property.