Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-31T04:02:43.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic structure in substitution tiling spaces

Published online by Cambridge University Press:  27 September 2012

MARCY BARGE  and
CARL OLIMB
MARCY BARGE
Affiliation:
Department of Mathematics, Montana State University, Bozeman, MT 59717, USA (email: barge@math.montana.edu)
CARL OLIMB
Affiliation:
Department of Mathematics, Southwest Minnesota State University, Marshall, MN 56258, USA (email: Carl.Olimb@smsu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Every sufficiently regular non-periodic space of tilings of 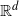$\mathbb {R}^d$ has at least one pair of distinct tilings that are asymptotic under translation in all the directions of some open 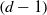$(d-1)$-dimensional hemisphere. If the tiling space comes from a substitution, there is a way of defining a location on such tilings at which asymptoticity ‘starts’. This leads to the definition of the branch locus of the tiling space: this is a subspace of the tiling space, of dimension at most 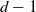$d-1$, that summarizes the ‘asymptotic in at least a half-space’ behavior in the tiling space. We prove that if a 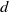$d$-dimensional self-similar substitution tiling space has a pair of distinct tilings that are asymptotic in a set of directions that contains a closed 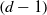$(d-1)$-hemisphere in its interior, then the branch locus is a topological invariant of the tiling space. If the tiling space is a two-dimensional self-similar Pisot substitution tiling space, the branch locus has a description as an inverse limit of an expanding Markov map on a zero- or one-dimensional simplicial complex.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 55 - 94
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[AP]Anderson, J. E. and Putnam, I. F.. Topological invariants for substitution tilings and their associated $C^*$-algebras. Ergod. Th. & Dynam. Sys. 18 (1998), 509–537.CrossRefGoogle Scholar
[BD]Barge, M. and Diamond, B.. A complete invariant for the topology of one-dimensional substitution tiling spaces. Ergod. Th. & Dynam. Sys. 21 (2001), 1333–1358.Google Scholar
[BD2]Barge, M. and Diamond, B.. Proximality in Pisot tiling spaces. Fund. Math. 194 (2007), 191–238.CrossRefGoogle Scholar
[BDH]Barge, M., Diamond, B. and Holton, C.. Asymptotic orbits of primitive substitutions. Theoret. Comput. Sci. 301 (2003), 439–450.Google Scholar
[BDHS]Barge, M., Diamond, B., Hunton, J. and Sadun, L.. Cohomology of substitution tiling spaces. Ergod. Th. & Dynam. Sys. 30 (2010), 1607–1627.Google Scholar
[BDS]Barge, M., Diamond, B. and Swanson, R.. The branch locus in one-dimensional substitution tiling spaces. Fund. Math. 204 (2009), 215–240.Google Scholar
[BKe]Barge, M. and Kellendonk, J.. Proximality and pure point spectrum for tiling dynamical systems, 2011, Preprint, arXiv:1108.4065.Google Scholar
[BL]Boyle, M. and Lind, D.. Expansive subdynamics. Trans. Amer. Math. Soc. 349(1) (1997), 55–102.Google Scholar
[BS]Barge, M. and Swanson, R.. Rigidity in one-dimensional tiling spaces. Top. Appl. 154(17) (2007), 3095–3099.Google Scholar
[BSa]Barge, M. and Sadun, L.. Quotient cohomology for tiling space. New York J. Math. 17 (2011), 579–599.Google Scholar
[BSW]Barge, M., Štimac, S. and Williams, R. F.. Pure discrete spectrum in substitution tiling spaces, 2011, Preprint, arXiv:1107.3598.Google Scholar
[FHK]Forrest, A., Hunton, J. and Kellendonk, J.. Topological invariants for projection method patterns. Mem. Amer. Math. Soc. 159(758) (2002).Google Scholar
[G-S]Goodman-Strauss, C.. Matching rules and substitution tilings. Ann. of Math. (2) 147(1) (1998), 181–223.Google Scholar
[H]Hochman, M.. Non-expansive directions for $\mathbb {Z}^2$ actions. Ergod. Th. & Dynam. Sys. 31(1) (2011), 91–112.Google Scholar
[K]Kwapisz, J.. Rigidity and mapping class group for abstract tiling spaces. Ergod. Th. & Dynam. Sys. 31(6) (2011), 1745–1783.Google Scholar
[M]Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math. 53 (1989), 139–186.Google Scholar
[O]Olimb, C.. The branch locus for two dimensional substitution tiling spaces. PhD Thesis, Montana State University, 2010.Google Scholar
[S]Sadun, L.. Topology of Tiling Spaces. American Mathematical Society, Providence, RI, 2008.Google Scholar
[So1]Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17 (1997), 695–738.Google Scholar
[So2]Solomyak, B.. Nonperiodicity implies unique composition for self-similar translationally finite tilings. Discrete Comput. Geom. 20 (1998), 265–279.Google Scholar
[So3]Solomyak, B.. Eigenfunctions for substitution tiling systems. Adv. Stud. Pure Math. 49 (2007), 433–454.Google Scholar
[W]Williams, R. F.. Classification of one-dimensional attractors. Proc. Symp. Pure Math. 14 (1970), 341–361.Google Scholar