Article contents
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
Published online by Cambridge University Press: 05 November 2020
Abstract
Let  ${\mathbf {G}}$ be a semisimple algebraic group over a number field K,
${\mathbf {G}}$ be a semisimple algebraic group over a number field K, 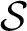 $\mathcal {S}$ a finite set of places of K,
$\mathcal {S}$ a finite set of places of K, 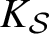 $K_{\mathcal {S}}$ the direct product of the completions
$K_{\mathcal {S}}$ the direct product of the completions 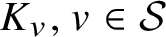 $K_{v}, v \in \mathcal {S}$, and
$K_{v}, v \in \mathcal {S}$, and 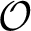 ${\mathcal O}$ the ring of
${\mathcal O}$ the ring of 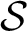 $\mathcal {S}$-integers of K. Let
$\mathcal {S}$-integers of K. Let 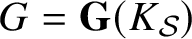 $G = {\mathbf {G}}(K_{\mathcal {S}})$,
$G = {\mathbf {G}}(K_{\mathcal {S}})$, 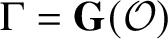 $\Gamma = {\mathbf {G}}({\mathcal O})$ and
$\Gamma = {\mathbf {G}}({\mathcal O})$ and 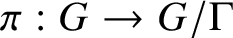 $\pi :G \rightarrow G/\Gamma $ the quotient map. We describe the closures of the locally divergent orbits
$\pi :G \rightarrow G/\Gamma $ the quotient map. We describe the closures of the locally divergent orbits 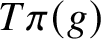 ${T\pi (g)}$ where T is a maximal
${T\pi (g)}$ where T is a maximal 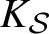 $K_{\mathcal {S}}$-split torus in G. If
$K_{\mathcal {S}}$-split torus in G. If 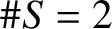 $\# S = 2$ then the closure
$\# S = 2$ then the closure 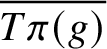 $ \overline{T\pi (g)}$ is a finite union of T-orbits stratified in terms of parabolic subgroups of
$ \overline{T\pi (g)}$ is a finite union of T-orbits stratified in terms of parabolic subgroups of  ${\mathbf {G}} \times {\mathbf {G}}$ and, consequently,
${\mathbf {G}} \times {\mathbf {G}}$ and, consequently, 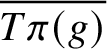 $\overline{T\pi (g)}$ is homogeneous (i.e.
$\overline{T\pi (g)}$ is homogeneous (i.e. 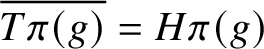 $\overline{T\pi (g)}= H\pi (g)$ for a subgroup H of G) if and only if
$\overline{T\pi (g)}= H\pi (g)$ for a subgroup H of G) if and only if 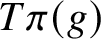 ${T\pi (g)}$ is closed. On the other hand, if
${T\pi (g)}$ is closed. On the other hand, if 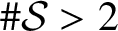 $\# \mathcal {S}> 2$ and K is not a
$\# \mathcal {S}> 2$ and K is not a 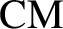 $\mathrm {CM}$-field then
$\mathrm {CM}$-field then 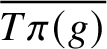 $\overline {T\pi (g)}$ is homogeneous for
$\overline {T\pi (g)}$ is homogeneous for 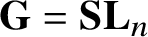 ${\mathbf {G}} = \mathbf {SL}_{n}$ and, generally, non-homogeneous but squeezed between closed orbits of two reductive subgroups of equal semisimple K-ranks for
${\mathbf {G}} = \mathbf {SL}_{n}$ and, generally, non-homogeneous but squeezed between closed orbits of two reductive subgroups of equal semisimple K-ranks for 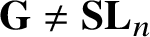 ${\mathbf {G}} \neq \mathbf {SL}_{n}$. As an application, we prove that
${\mathbf {G}} \neq \mathbf {SL}_{n}$. As an application, we prove that 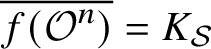 $\overline {f({\mathcal O}^{n})} = K_{\mathcal {S}}$ for the class of non-rational locally K-decomposable homogeneous forms
$\overline {f({\mathcal O}^{n})} = K_{\mathcal {S}}$ for the class of non-rational locally K-decomposable homogeneous forms 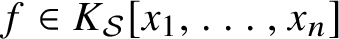 $f \in K_{\mathcal {S}}[x_1, \ldots , x_{n}]$.
$f \in K_{\mathcal {S}}[x_1, \ldots , x_{n}]$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by


