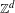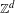Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DANILENKO, ALEXANDRE I.
2017.
Directional recurrence and directional rigidity for infinite measure preserving actions of nilpotent lattices.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 6,
p.
1841.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Wu, Haiyan
and
Li, Zhiming
2022.
Ergodic theorems for capacity preserving Z+d-actions.
International Journal of Approximate Reasoning,
Vol. 146,
Issue. ,
p.
1.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2023.
Ergodic Theory.
p.
233.
Robinson, E. Arthur
Rosenblatt, Joseph
and
Şahi̇n, Ayşe A.
2024.
Directional ergodicity, weak mixing and mixing for Zd- and Rd-actions.
Indagationes Mathematicae,
Vol. 35,
Issue. 5,
p.
837.