Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MILLER, BENJAMIN
2008.
The existence of measures of a given cocycle, II: probability measures.
Ergodic Theory and Dynamical Systems,
Vol. 28,
Issue. 5,
p.
1615.
Andretta, Alessandro
and
Camerlo, Riccardo
2013.
The descriptive set theory of the Lebesgue Density Theorem.
Advances in Mathematics,
Vol. 234,
Issue. ,
p.
1.
Bianchi, Alessandra
Cristadoro, Giampaolo
Lenci, Marco
and
Ligabò, Marilena
2016.
Random Walks in a One-Dimensional Lévy Random Environment.
Journal of Statistical Physics,
Vol. 163,
Issue. 1,
p.
22.
Ganguly, Arijit
and
Ghosh, Anish
2017.
Dirichlet's Theorem in Function Fields.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 3,
p.
532.
Kjos-Hanssen, Bjørn
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
599.
KJOS-HANSSEN, BJØRN
2018.
PERMUTATIONS OF THE INTEGERS INDUCE ONLY THE TRIVIAL AUTOMORPHISM OF THE TURING DEGREES.
The Bulletin of Symbolic Logic,
Vol. 24,
Issue. 2,
p.
165.
Andretta, Alessandro
Camerlo, Riccardo
and
Costantini, Camillo
2019.
Lebesgue density and exceptional points.
Proceedings of the London Mathematical Society,
Vol. 118,
Issue. 1,
p.
103.
MILLER, BENJAMIN D.
2020.
On the existence of cocycle-invariant Borel probability measures.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 11,
p.
3150.
INSELMANN, MANUEL J.
and
MILLER, BENJAMIN D.
2021.
RECURRENCE AND THE EXISTENCE OF INVARIANT MEASURES.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 1,
p.
60.
LOPES, ARTUR O.
and
MENGUE, JAIRO K.
2021.
Thermodynamic formalism for Haar systems in noncommutative integration: transverse functions and entropy of transverse measures.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 6,
p.
1835.
de Castro, G. G.
Lopes, Artur O.
and
Mantovani, G.
2021.
Modeling, Dynamics, Optimization and Bioeconomics IV.
Vol. 365,
Issue. ,
p.
79.
Müller, Sandra
Schlicht, Philipp
Schrittesser, David
and
Weinert, Thilo
2022.
Lebesgue’s density theorem and definable selectors for ideals.
Israel Journal of Mathematics,
Vol. 249,
Issue. 2,
p.
501.
Feng, De-Jun
2023.
Dimension of invariant measures for affine iterated function systems.
Duke Mathematical Journal,
Vol. 172,
Issue. 4,
HURDER, Steven
and
LUKINA, Olga
2025.
Essential holonomy of Cantor actions.
Journal of the Mathematical Society of Japan,
Vol. 77,
Issue. 1,

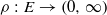 , we characterize the circumstances under which there is a suitably non-trivial
, we characterize the circumstances under which there is a suitably non-trivial 