No CrossRef data available.
Article contents
Expansion properties of double standard maps
Published online by Cambridge University Press: 05 July 2022
Abstract
For the family of double standard maps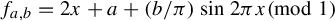 
$f_{a,b}=2x+a+({b}/{\pi }) \sin 2\pi x \pmod {1}$ we investigate the structure of the space of parameters a when 
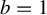$b=1$ and when 
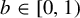$b\in [0,1)$. In the first case the maps have a critical point, but for a set of parameters 
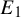$E_1$ of positive Lebesgue measure there is an invariant absolutely continuous measure for 
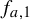$f_{a,1}$. In the second case there is an open non-empty set 
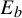$E_b$ of parameters for which the map 
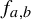$f_{a,b}$ is expanding. We show that as 
$b\nearrow 1$, the set 
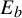$E_b$ accumulates on many points of 
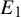$E_1$ in a regular way from the measure point of view.
MSC classification
Primary:
37E10: Maps of the circle
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Arnold, V. I.. Small denominators. I. Mappings of the circumference onto itself. Amer. Math. Soc. Transl. 46 (1965), 213–284.Google Scholar
Benedicks, M. and Carleson, L.. On iterations of
$1-a{x}^2$
on
$\left(-1,1\right)$
. Ann. of Math. (2) 122(1) (1985), 1–25.CrossRefGoogle Scholar
$1-a{x}^2$
on
$\left(-1,1\right)$
. Ann. of Math. (2) 122(1) (1985), 1–25.CrossRefGoogle ScholarBenedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2) 133(1) (1991), 73–169.10.2307/2944326CrossRefGoogle Scholar
Benedicks, M. and Rodrigues, A.. Kneading sequences for double standard maps. Fund. Math. 206 (2009), 61–75.CrossRefGoogle Scholar
Bruin, H., Luzzatto, S. and van Strien, S.. Decay of correlations in one-dimensional dynamics. Ann. Sci. Éc. Norm. Supér. (4) 36(4) (2003), 621–646.CrossRefGoogle Scholar
Bruin, H., Rivera-Letelier, J., van Strien, S. and Shen, W.. Large derivatives, backward contraction and invariant densities for interval maps. Invent. Math. 172(3) (2008), 509–533.CrossRefGoogle Scholar
Collet, P. and Eckmann, J.-P.. On the abundance of aperiodic behaviour for maps on the interval. Comm. Math. Phys. 73 (1980) 115–160.CrossRefGoogle Scholar
de Melo, W. and van Strien, S.. One-Dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 25). Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
Dezotti, A.. Connectedness of the Arnold tongues for double standard maps. Proc. Amer. Math. Soc. 138 (2010), 3569–3583.CrossRefGoogle Scholar
Fagella, N. and Garijo, A.. The parameter planes of
$\lambda {z}^m\exp (z)$
for
$m\ge 2$
. Comm. Math. Phys. 273 (2007), 755–783.10.1007/s00220-007-0265-8CrossRefGoogle Scholar
$\lambda {z}^m\exp (z)$
for
$m\ge 2$
. Comm. Math. Phys. 273 (2007), 755–783.10.1007/s00220-007-0265-8CrossRefGoogle ScholarJakobson, M.. Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Comm. Math. Phys. 81 (1981), 39–88.CrossRefGoogle Scholar
Krzyżewski, K. and Szlenk, W.. On invariant measures for expanding differentiable mappings. Studia Math. 33 (1969), 83–92.CrossRefGoogle Scholar
Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.10.1090/S0002-9947-1973-0335758-1CrossRefGoogle Scholar
Levin, G. and Świątek, G.. Universality of critical circle covers. Comm. Math. Phys. 228 (2002), 371–399.CrossRefGoogle Scholar
Levin, G. and van Strien, S.. Bounds for maps of an interval with one critical point of inflection type. II. Invent. Math. 141(2) (2000), 399–465.CrossRefGoogle Scholar
Mañé, R.. Hyperbolicity, sinks and measure in one-dimensional dynamics. Comm. Math. Phys. 100 (1985), 495–524.CrossRefGoogle Scholar
Misiurewicz, M.. Absolutely continuous measures for certain maps of an interval. Publ. Math. Inst. Hautes Études Sci. 53 (1981), 17–51.10.1007/BF02698686CrossRefGoogle Scholar
Misiurewicz, M.,Iooss, G.,Helleman, R. H. G. andStora, R. (eds.)Maps of an interval. Chaotic Behaviour of Deterministic Systems. North-Holland, Amsterdam, 1983, pp. 565–590.Google Scholar
Misiurewicz, M. and Rodrigues, A.. Double standard maps. Comm. Math. Phys. 273 (2007), 37–65.CrossRefGoogle Scholar
Misiurewicz, M. and Rodrigues, A.. On the tip of the tongue. J. Fixed Point Theory Appl. 3 (2008), 131–141.CrossRefGoogle Scholar
Misiurewicz, M. and Rodrigues, A.. Non-generic cusps. Trans. Amer. Math. Soc. 363 (2011), 3553–3572.CrossRefGoogle Scholar
Nowicki, T. and van Strien, S.. Absolutely continuous invariant measures for
${C}^2$
unimodal maps satisfying the Collet–Eckmann conditions. Invent. Math. 93 (1988), 619–635.CrossRefGoogle Scholar
${C}^2$
unimodal maps satisfying the Collet–Eckmann conditions. Invent. Math. 93 (1988), 619–635.CrossRefGoogle ScholarShub, M. and Sullivan, D.. Expanding endomorphisms of the circle revisited. Ergod. Th. & Dynam. Sys. 5 (1985), 285–289.CrossRefGoogle Scholar
Thieullen, P., Tresser, C. and Young, L.-S.. Positive Lyapunov exponent for generic one-parameter families of unimodal maps. J. Anal. Math. 64 (1994), 121–172.CrossRefGoogle Scholar
van Strien, S.. Hyperbolicity and invariant measures for general
${C}^2$
interval maps satisfying the Misiurewicz condition. Comm. Math. Phys. 128 (1990), 437–496.CrossRefGoogle Scholar
${C}^2$
interval maps satisfying the Misiurewicz condition. Comm. Math. Phys. 128 (1990), 437–496.CrossRefGoogle Scholar