No CrossRef data available.
Article contents
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
Part of:
Noncompact transformation groups
Stochastic processes
Graph theory
Ergodic theory
Equilibrium statistical mechanics
Published online by Cambridge University Press: 22 December 2022
Abstract
We give an example of an FIID vertex-labeling of 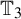 ${\mathbb T}_3$ whose marginals are uniform on
${\mathbb T}_3$ whose marginals are uniform on 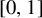 $[0,1]$, and if we delete the edges between those vertices whose labels are different, then some of the remaining clusters are infinite. We also show that no such process can be finitary.
$[0,1]$, and if we delete the edges between those vertices whose labels are different, then some of the remaining clusters are infinite. We also show that no such process can be finitary.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Angel, O., Ray, G. and Spinka, Y.. Uniform even subgraphs and graphical representations of Ising as factors of i.i.d. Preprint, 2021, arXiv:2112.03228.Google Scholar
Bollobás, B.. The independence ratio of regular graphs. Proc. Amer. Math. Soc. 83 (1981), 433–436.CrossRefGoogle Scholar
Bowen, L.. A brief introduction to sofic entropy theory. Proceedings of ICM (Rio de Janeiro 2018). Vol. III. Eds. Sirakov, B., Ney de Souza, P. and Viana, M.. World Scientific, Singapore, 2018, pp. 1847–1866. Preprint, 2017, available at https://arxiv.org/abs/1711.02062.Google Scholar
Benjamini, I., Lyons, R., Peres, Y. and Schramm, O.. Group-invariant percolation on graphs. Geom. Funct. Anal. 9 (1999), 29–66.CrossRefGoogle Scholar
Backhausz, Á., Szegedy, B. and Virág, B.. Ramanujan graphings and correlation decay in local algorithms. Random Structures Algorithms 47 (2015), 424–435.10.1002/rsa.20562CrossRefGoogle Scholar
Chifan, I. and Ioana, A.. Ergodic subequivalence relations induced by a Bernoulli action. Geom. Funct. Anal. 20 (2010), 53–67.10.1007/s00039-010-0058-7CrossRefGoogle Scholar
Gaboriau, D.. Orbit equivalence and measured group theory. Proceedings of the ICM (Hyderabad, India, 2010). Vol. III. Eds. Bhatia, R., Pal, A., Rangarajan, G., Srinivas, V. and Vanninathan, M.. Hindustan Book Agency (India), India and World Scientific, Singapore, 2010, pp. 1501–1527.Google Scholar
Gaboriau, D. and Lyons, R.. A measurable-group-theoretic solution to von Neumann’s problem. Invent. Math. 177 (2009), 533–540.CrossRefGoogle Scholar
Keane, M. and Smorodinsky, M.. Bernoulli schemes of the same entropy are finitarily isomorphic. Ann. of Math. (2) 109(2) (1979), 397–406.10.2307/1971117CrossRefGoogle Scholar
Lyons, R. and Peres, Y.. Probability on Trees and Networks. Cambridge University Press, Cambridge, 2016. Available at http://mypage.iu.edu/rdlyons.CrossRefGoogle Scholar
Lyons, R. and Schramm, O.. Indistinguishability of percolation clusters. Ann. Probab. 27 (1999), 1809–1836.10.1214/aop/1022874816CrossRefGoogle Scholar
Meshalkin, L. D.. A case of isomorphism of Bernoulli schemes. Dokl. Akad. Nauk SSSR 128 (1959), 41–44.Google Scholar
Meyerovitch, T. and Spinka, Y.. Entropy-efficient finitary codings. Preprint, 2022, arXiv:2201.06542.Google Scholar
Nam, D., Sly, A. and Zhang, L.. Ising model on trees and factors of IID. Comm. Math. Phys. 389 (2022), 1009–1046.CrossRefGoogle Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.10.1007/BF02790325CrossRefGoogle Scholar
Pete, G.. Probability and Geometry on Groups. Book in preparation. http://www.math.bme.hu/gabor/PGG.pdf.Google Scholar
Ray, G. and Spinka, Y.. Graphical representations and gradients of Ising as factors of i.i.d. Talk at the Percolation Today Webinar, January 18, 2022. Accessible from https://percolation.ethz.ch/.Google Scholar
Rahman, M. and Virág, B.. Local algorithms for independent sets are half-optimal. Ann. Probab. 45 (2017), 1543–1577.CrossRefGoogle Scholar
Serafin, J.. Finitary codes, a short survey. Dynamics & Stochastics (Institute of Mathematical Statistics Lecture Notes—Monograph Series, 48). Eds. Denteneer, D., den Hollander, F. and Verbitskiy, E.. Institute of Mathematical Statistics, Beachwood, OH, 2006, pp. 262–273.CrossRefGoogle Scholar
Sly, A.. Computational transition at the uniqueness threshold. Proc. 2010 IEEE 51st Annual Symposium on Foundations of Computer Science. IEEE Computer Society, Piscataway, NJ, 2010, pp. 287–296. Available at https://arxiv.org/abs/1005.5584.Google Scholar
Spinka, Y.. Finitary codings for spatial mixing Markov random fields. Ann. Probab. 48 (2020), 1557–1591.10.1214/19-AOP1405CrossRefGoogle Scholar
van den Berg, J. and Steif, J. E.. On the existence and nonexistence of finitary codings for a class of random fields. Ann. Probab. 27 (1999), 1501–1522.Google Scholar



