Hostname: page-component-7f64f4797f-zzvtc Total loading time: 0 Render date: 2025-11-04T08:09:55.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalizations of Furstenberg’s Diophantine result

Published online by Cambridge University Press:  20 September 2016

ASAF KATZ
ASAF KATZ*
Affiliation:
Einstein Institute of Mathematics, The Hebrew University of Jerusalem, Jerusalem, 91904, Israel email asaf.katz@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove two generalizations of Furstenberg’s Diophantine result regarding the density of an orbit of an irrational point in the $1$ -torus under the action of multiplication by a non-lacunary multiplicative semigroup of 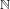$\mathbb{N}$ . We show that for any sequences 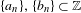$\{a_{n}\},\{b_{n}\}\subset \mathbb{Z}$ for which the quotients of successive elements tend to $1$ as $n$ goes to infinity, and any infinite sequence 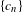$\{c_{n}\}$ , the set 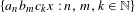$\{a_{n}b_{m}c_{k}x:n,m,k\in \mathbb{N}\}$ is dense modulo $1$ for every irrational $x$ . 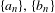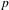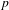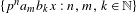Moreover, by ergodic-theoretical methods, we prove that if $\{a_{n}\},\{b_{n}\}$ are a sequence having smooth $p$ -adic interpolation for some prime number $p$ , then for every irrational $x$ , the sequence $\{p^{n}a_{m}b_{k}x:n,m,k\in \mathbb{N}\}$ is dense modulo 1.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 3 , May 2018 , pp. 1012 - 1024
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Boshernitzan, M. D.. Density modulo 1 of dilations of sublacunary sequences. Adv. Math. 108(1) (1994), 104–117.CrossRefGoogle Scholar
Boshernitzan, M. D.. Elementary proof of Furstenberg’s Diophantine result. Proc. Amer. Math. Soc. 122(1) (1994), 67–70.Google Scholar
Bourgain, J., Lindenstrauss, E., Michel, P. and Venkatesh, A.. Some effective results for × a × b . Ergod. Th. & Dynam. Sys. 29(6) (2009), 1705–1722.CrossRefGoogle Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E.. Invariant measures and the set of exceptions to Littlewood’s conjecture. Ann. of Math. (2) 164(2) (2006), 513–560.CrossRefGoogle Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.CrossRefGoogle Scholar
Gorodnik, A. and Kadyrov, S.. Algebraic numbers, hyperbolicity, and density modulo one. J. Number Theory 132(11) (2012), 2499–2509.CrossRefGoogle Scholar
Host, B.. Nombres normaux, entropie, translations. Israel J. Math. 91(1–3) (1995), 419–428.CrossRefGoogle Scholar
Host, B.. Some results of uniform distribution in the multidimensional torus. Ergod. Th. & Dynam. Sys. 20(02) (2000), 439–452.CrossRefGoogle Scholar
Johnson, A. S. A.. Measures on the circle invariant under multiplication by a nonlacunary subsemigroup of the integers. Israel J. Math. 77(1–2) (1992), 211–240.CrossRefGoogle Scholar
Kra, B.. A generalization of Furstenberg’s diophantine theorem. Proc. Amer. Math. Soc. 127(7) (1999), 1951–1956.CrossRefGoogle Scholar
Lindenstrauss, E.. p-adic foliation and equidistribution. Israel J. Math. 122(1) (2001), 29–42.CrossRefGoogle Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Sspaces: Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44) . Cambridge University Press, Cambridge, 1999.Google Scholar
Meiri, D.. Entropy and uniform distribution of orbits in T d . Israel J. Math. 105 (1998), 155–183.CrossRefGoogle Scholar
Robert, A. M.. A Course in p-adic Analysis (Graduate Texts in Mathematics, 198) . Springer, New York, 2000.CrossRefGoogle Scholar
Schwartzman, S.. On transformation groups. PhD Thesis, Yale University, 1952.Google Scholar
Urban, R.. Algebraic numbers and density modulo 1. J. Number Theory 128(3) (2008), 645–661.CrossRefGoogle Scholar
Urban, R.. Sequences of algebraic numbers and density modulo 1. Publ. Math. Debrecen 72(1) (2008), 141–154.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Vol. 79. Springer, New York, 2000.Google Scholar