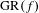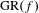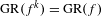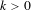Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abdelli, Hafedh
and
Askri, Ghassen
2019.
Chain recurrent points of monotone graph maps and CR-Pm property on local dendrites.
Journal of Difference Equations and Applications,
Vol. 25,
Issue. 1,
p.
119.
Bernardi, Olga
and
Florio, Anna
2019.
Existence of Lipschitz continuous Lyapunov functions strict outside the strong chain recurrent set.
Dynamical Systems,
Vol. 34,
Issue. 1,
p.
71.
Bernardi, Olga
Florio, Anna
and
Wiseman, Jim
2020.
The Generalized Recurrent Set, Explosions and Lyapunov Functions.
Journal of Dynamics and Differential Equations,
Vol. 32,
Issue. 4,
p.
1797.
Ahmadi, Seyyed Alireza
2024.
Strong Chain Transitivity via Uniformity.
Qualitative Theory of Dynamical Systems,
Vol. 23,
Issue. 3,
Viscovini, Eduardo C.
and
Souza, Josiney A.
2024.
A dispersive dynamical system that is chain transitive.
Examples and Counterexamples,
Vol. 6,
Issue. ,
p.
100153.
De Leo, Roberto
and
Yorke, James A.
2025.
Streams and Graphs of Dynamical Systems.
Qualitative Theory of Dynamical Systems,
Vol. 24,
Issue. 1,
Darban Maghami, Nooshin
Ahmadi, Seyyed Alireza
and
Shabani, Zahra
2025.
Strong chain transitivity in hyperspaces of uniform spaces.
Applied General Topology,
Vol. 26,
Issue. 1,
p.
115.