Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-12T06:48:41.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic rotation sets

Part of: Low-dimensional dynamical systems Ergodic theory

Published online by Cambridge University Press:  29 December 2020

SEBASTIÁN PAVEZ-MOLINA
SEBASTIÁN PAVEZ-MOLINA*
Affiliation:
Facultad de Matemáticas, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna, 4860Santiago, Chile
*
e-mail:snpavez@uc.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 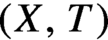$(X,T)$ be a topological dynamical system. Given a continuous vector-valued function 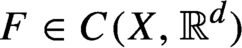$F \in C(X, \mathbb {R}^{d})$ called a potential, we define its rotation set 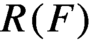$R(F)$ as the set of integrals of F with respect to all T-invariant probability measures, which is a convex body of 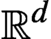$\mathbb {R}^{d}$ . In this paper we study the geometry of rotation sets. We prove that if T is a non-uniquely ergodic topological dynamical system with a dense set of periodic measures, then the map 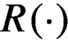$R(\cdot )$ is open with respect to the uniform topologies. As a consequence, we obtain that the rotation set of a generic potential is strictly convex and has 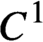$C^{1}$ boundary. Furthermore, we prove that the map 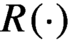$R(\cdot )$ is surjective, extending a result of Kucherenko and Wolf.

Keywords

generalized rotation settopological dynamicsconvexity

MSC classification

Primary: 37A99: None of the above, but in this section
Secondary: 37E45: Rotation numbers and vectors
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 1 , January 2022 , pp. 250 - 262
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bochi, J.. Ergodic optimization of Birkhoff averages and Lyapunov exponents. Proceedings of the International Congress of Mathematicians: Rio de Janeiro 2018. Vol. 2. Ed. Boyan, S., de Souza, P. N. and Viana, M.. World Scientific, Singapore, 2019, pp. 1821–1842.Google Scholar
Boyland, P., Carvalho, A. and Hall, T.. New rotation sets in a family of torus homeomorphisms. Invent. Math. 204 (2016), 895–937.CrossRefGoogle Scholar
Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 489–508.CrossRefGoogle Scholar
Bousch, T.. Um lemme de Mañé bilatéral. C. R. Math. 335 (2002), 533–536.CrossRefGoogle Scholar
Conze, J.P. and Guirvac’h, Y.. Croissance des sommes ergodiques et principe variationnel. Unpublished manuscript, circa 1993.Google Scholar
Gelfert, K. and Kwietniak, D.. On density of ergodic measures and generic points. Ergod. Th. & Dynam. Sys. 38(5) (2018), 1745–1767.CrossRefGoogle Scholar
Jenkinson, O.. Conjugacy rigidity, cohomological triviality, and barycentres of invariant measures. PhD Thesis, University of Warwick, 1996.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.CrossRefGoogle Scholar
Jenkinson, O.. Every ergodic measure is uniquely maximizing. Discrete Contin. Dyn. Syst. 16 (2006), 383–392.CrossRefGoogle Scholar
Jenkinson, O.. Ergodic optimization in dynamical systems. Ergod. Th. & Dynam. Sys. 39(10) (2019), 2593–2618.CrossRefGoogle Scholar
Kucherenko, T. and Wolf, C.. Geometry and entropy of generalized rotation sets. Israel J. Math. 199 (2014), 791–829 CrossRefGoogle Scholar
Klima, V. and Netuka, I.. Smoothness of a typical convex function. Czechoslov. Math. J. 31(4) (1981), 569–572.CrossRefGoogle Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. (2) 40(3) (1989), 490–506.CrossRefGoogle Scholar
Passegi, A.. Rational polygons as rotation sets of generic homeomorphisms of the two torus. J. Lond. Math. Soc. 89(1) (2014), 235–254.CrossRefGoogle Scholar
Savchenko, S. V.. Homological inequalities for finite topological Markov chains. Funct. Anal. Appl. 33(3) (1999), 236–238.CrossRefGoogle Scholar
Schneider, R.. Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, New York, 2014.Google Scholar
Ziemian, K. Rotation sets for subshifts of finite type. Fund. Math. 146(2) (1995), 189–201.Google Scholar