Article contents
A good universal weight for nonconventional ergodic averages in norm
Published online by Cambridge University Press: 28 December 2015
Abstract
We will show that the sequence appearing in the double recurrence theorem is a good universal weight for the Furstenberg averages. That is, given a system 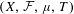 $(X,{\mathcal{F}},\unicode[STIX]{x1D707},T)$ and bounded functions
$(X,{\mathcal{F}},\unicode[STIX]{x1D707},T)$ and bounded functions 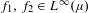 $f_{1},f_{2}\in L^{\infty }(\unicode[STIX]{x1D707})$ , there exists a set of full-measure
$f_{1},f_{2}\in L^{\infty }(\unicode[STIX]{x1D707})$ , there exists a set of full-measure  $X_{f_{1},f_{2}}$ in
$X_{f_{1},f_{2}}$ in 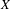 $X$ that is independent of integers
$X$ that is independent of integers  $a$ and
$a$ and 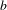 $b$ and a positive integer
$b$ and a positive integer 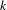 $k$ such that, for all
$k$ such that, for all 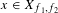 $x\in X_{f_{1},f_{2}}$ , for every other measure-preserving system
$x\in X_{f_{1},f_{2}}$ , for every other measure-preserving system 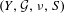 $(Y,{\mathcal{G}},\unicode[STIX]{x1D708},S)$ and for each bounded and measurable function
$(Y,{\mathcal{G}},\unicode[STIX]{x1D708},S)$ and for each bounded and measurable function 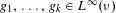 $g_{1},\ldots ,g_{k}\in L^{\infty }(\unicode[STIX]{x1D708})$ , the averages
$g_{1},\ldots ,g_{k}\in L^{\infty }(\unicode[STIX]{x1D708})$ , the averages 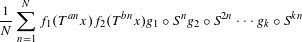 $$\begin{eqnarray}\frac{1}{N}\mathop{\sum }_{n=1}^{N}f_{1}(T^{an}x)f_{2}(T^{bn}x)g_{1}\circ S^{n}g_{2}\circ S^{2n}\cdots g_{k}\circ S^{kn}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{N}\mathop{\sum }_{n=1}^{N}f_{1}(T^{an}x)f_{2}(T^{bn}x)g_{1}\circ S^{n}g_{2}\circ S^{2n}\cdots g_{k}\circ S^{kn}\end{eqnarray}$$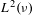 $L^{2}(\unicode[STIX]{x1D708})$ .
$L^{2}(\unicode[STIX]{x1D708})$ .
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 3
- Cited by

